Dedication
Judy Paterson sadly passed away during this research project. However, her contribution was a major one, co-leading the design and grant application team, taking responsibility for the Team-Based Learning innovation, conducting interviews, and contributing strongly in several of the learning output observation groups.
We dedicate this report to her memory.
– Bill
Overview of the project
The LUMOS Project had two parts: the development of three innovative methods of undergraduate mathematics course delivery, and the identification and observation of a wide range of desired learning outcomes. This project sought to link these aspects.
The research questions were:
- What practical, pedagogical, administrative and curricular barriers need to be overcome to establish each of the three innovations for undergraduate mathematics course delivery?
- How do the learning outcomes of students who are taught in each of the three innovations compare with those of students in conventionally structured undergraduate courses?
- How can we construct a comprehensive description of learning outcomes at upper undergraduate level?
- What practical and validated evaluation instruments can be found or constructed for the learning outcomes identified in c)?
Innovative delivery methods
The three innovative course delivery methods developed were: Team-Based Learning Mode, Intensive Technology Mode, and Low Lecture Mode. They were developed as alternatives to the standard delivery mode at the University of Auckland (three lectures and a tutorial per week, assignments, term test, and examination).
Team-Based Learning is a well-defined technique, initiated in Business Schools, first in the USA and then more widely, see “How To” Guide #1: Implement teambased learning. There is a considerable literature about its use in this context, but little was found about its use in mathematics courses. The main components of this method are the Reading Assessment Tests (RATs) and a higher than usual amount of classwork carried out in groups. The RATs involve pre-reading and then an individual followed by a group attempt at a shortanswer test based on the reading. The effect is to ensure pre-reading is done and stimulate debate on its contents. This is adapted to a mathematical setting by including mathematical tasks as well as a reading on the relevant mathematical topic.
The Team-Based Learning mode was successfully adapted, and was trialled over several different courses more than once over the three-year project, and continues to be used in Foundation, 300-level, and post-graduate level courses. It is also used in a Mathematics Education course offered by the Mathematics Department. In all cases, it is fully implemented as an alternative mode, and is extremely popular with both lecturers and students. Course results are more or less similar to pre-innovation results; all courses get higher than normal student evaluations; and the lecturers involved like this style of delivery. Some positive attitudinal effects can be observed. The study concluded that Team-Based Learning modes occupying at least one lecture every two weeks are useful additions to an undergraduate teaching repertoire.
The Intensive Technology Mode involves the use of technology to the fullest extent possible for the course: as a means of delivery; as a lecturing tool; as a student learning aid; and as an assessment mechanism.
The Intensive Technology mode was not fully implemented, although technology was a large part of delivery for one course over two years. While generally successful, difficulties occurred, such as availability of laboratories for large class assessments. Some attempts were made to incorporate new technology-based teaching styles and encourage higher student use of technology. These attempts also sometimes foundered on institutional difficulties, and sustainability was highly lecturer dependent. Student responses were not always positive, although impact on student grades was neutral. The barriers to higher technology use are welldocumented. Our study concluded that implementing technology needs to be done with caution, in small steps, with considerable support for lecturers, and addressing the change of learning culture required. Equity issues, as noted in the literature, remain.
The Low Lecture Mode is based on the idea that students can be more responsible for their own learning for much of the course material, and that undergraduates need to be inducted to authentic mathematical experiences, see “How To” Guide #2: Implement semi-authentic mathematical experiences and “How To” Guide #3: Shift responsbility for learning onto students. Hence there is only one lecture per week (if that) and this lecture is about the course. Rather than specifically go over mathematical techniques and content, the lecture covers why it is important, how it is connected, gives historical background, discusses applications, or diverges onto the underlying ideas behind the topic. Students are guided to on-line and text resources, and exactly what learning they must undertake for themselves, and are provided with selfmonitoring tests by which they can check their learning. In addition, assignments are replaced by Engagement Sessions where students work, both individually and in guided small groups, on open-ended mathematical situations and write up their deliberations in a report.
The Low Lecture mode was trialled on three different occasions, in each case as a voluntary stream of the large 100-level mathematics course for nonmajors (there are 2 to 4 other streams of this course, depending on the semester). On each occasion, the numbers taking part in the trial were too small for strong comparisons with the normal mode to be made. Nevertheless, because of the parallel nature of the trial, we have the most information about this mode. The style of delivery attracted and suited some types of students more than others: mature students and parttime students made up many of the volunteers, mainly because of the more flexible schedule. The mode was most successful with well-motivated and well-organised students, with significant improvements on attitudes over normal delivery, and grades equal or better. The students who reverted to normal modes were generally less organised and motivated. The single lecture and the Engagement Sessions were both highly appreciated (by students, by the lecturers, and by the international observers). Student grades for the course were not significantly different overall in either direction between those in the normal and those in the Low Lecture streams, when corrected for expected attainment. Attitudinally, however, Low Lecture students showed more positive gains, although this might be expected due to experimental effects. This study concluded that further implementation of the Low Lecture trial would best be achieved by introducing two or three “about mathematics” lectures, and one Engagement Session as part of the normal delivery, rather than having an alternative stream or making any one course a “Low Lecture” delivery.
occasions, in each case as a voluntary stream of the large 100-level mathematics course for nonmajors (there are 2 to 4 other streams of this course, depending on the semester). On each occasion, the numbers taking part in the trial were too small for strong comparisons with the normal mode to be made. Nevertheless, because of the parallel nature of the trial, we have the most information about this mode. The style of delivery attracted and suited some types of students more than others: mature students and parttime students made up many of the volunteers, mainly because of the more flexible schedule. The mode was most successful with well-motivated and well-organised students, with significant improvements on attitudes over normal delivery, and grades equal or better. The students who reverted to normal modes were generally less organised and motivated. The single lecture and the Engagement Sessions were both highly appreciated (by students, by the lecturers, and by the international observers). Student grades for the course were not significantly different overall in either direction between those in the normal and those in the Low Lecture streams, when corrected for expected attainment. Attitudinally, however, Low Lecture students showed more positive gains, although this might be expected due to experimental effects. This study concluded that further implementation of the Low Lecture trial would best be achieved by introducing two or three “about mathematics” lectures, and one Engagement Session as part of the normal delivery, rather than having an alternative stream or making any one course a “Low Lecture” delivery.
Desired learning outcomes
Although undergraduate mathematics assessment gives us a picture of the content and skills learned by students, there are other outcomes that stakeholders hope for when a student has completed a Bachelor’s degree in mathematics. Not only lecturers, but employers, students themselves, and the university (by way of its graduate outcomes) have ideas on what students should learn and how students might develop. Our first task was to identify and categorise these outcomes. We undertook both literature searches and thirty-five interviews, the majority of which were with lecturers, to produce a catalogue of Undergraduate Learning Outcomes.
The resulting Learning Outcome Spectrum was developed to include all suggested outcomes grouped into three categories: Mathematical Content; Skills, Processes and Behaviours; and Affective Outcomes. We are convinced that a significant improvement of reporting on course outcomes can be achieved with easily managable time- and resource-inputs.
Mathematical Content was further subdivided into “Knowing That” and “Deeper Understanding”. The Skills and Behaviours category included not only routine skills, but also mathematical habits of mind, and higher learning habits that might apply to other disciplines. The Affective category took the most analysis and resulted in a new dimension of affect not found in the literature, namely “Respect and Usefulness”. This dimension replaced “A Liking for Mathematics”, which is a common dimension at primary and secondary school level, but was not mentioned by a single respondent as a desirable outcome—possibly because it is assumed at university level. The Affective category also includes beliefs about mathematics learning.
Most of these desired outcomes are not routinely observed in that very few undergraduate courses mention such outcomes in their documentation, nor are they evident in assessment instruments. The next task, therefore, was to develop practical instruments that lecturers could use to observe the development of these outcomes over the period of a course. We were focused on class outcomes rather than individual assessments, and the instruments needed to be sensitive enough to indicate progress (or not) over the period of a semester.
The development of observation instruments varied. Mathematical content and routine skills are adequately (consistently and reliably) observed using conventional test and examinations, particularly if taken as class data. Indeed, this study concluded that much more use could be made of aggregated data to analyse course effectiveness of these outcomes (i.e. there is a place for advanced learning analytics for this purpose).
To our surprise, the development of an observation instrument for Affect was fully achieved very early in the project. This enabled us to use it on several occasions and confirm that the instrument was not only sensitive to indicate progress over a course, but also gave consistent and differing profiles for each course on which it was trialled, including different levels of undergraduate mathematics and an Engineering mathematics course. The instrument is surprisingly simple—a twelve-question on-line survey that takes less than two minutes. It does not require full class participation to achieve good results.
The further learning outcome for which an instrument was developed was mathematical communication. However, this instrument, while relatively easy to use, does need prior training for effective use. It takes the form of a schedule to be used in a group-work tutorial.
The three outcomes for which observation instruments were developed to trial stage were Conceptual Readiness, Mathematical Persistence, and Mathematical Foresight. The first and last are the subject of on-going research projects with international involvement, with the Conceptual Readiness instrument at a welldeveloped stage. Initial progress has been made on Mathematical Versatility, Hypothesising, and Modelling. In the case of the first and last, as well as for the learning outcomes of Mathematical Creativity and Mathematical Proving, there is a considerable literature, and some methods of observing these outcomes in individual students. The adaptation of such methods to practical class-size, and sensitive observations has not yet been achieved. No progress was made on wider learning behaviours such as those described in graduate outcome documents. This study regards continued development of these instruments as important work, and urges a start be made on ways to observe whether graduate outcomes are affected by individual courses.
Linking course delivery to learning outcomes
Making a connection between teaching methods and the achievement of learning outcomes is the Holy Grail of educational research, and unlikely to be comprehensively achieved. Nevertheless, progress in the quest has resulted in finding a few treasures, for example a highly polished cup that reflected the drinker’s emotions and a new recipe for a potion that prepares you for new ideas. We also found evidence of the existence and characteristics of the Holy Grail, and pathways that are likely to lead later searchers closer to their goal.
In particular, we aimed to produce a Course Learning Profile, that is, a document that would summarise a fuller range of Learning Outcomes than those that are currently normally reported upon, including the quantitative and qualitative evidence available. The structure of the Course Learning Profile does not enable course delivery methods to be ranked from best to worst, rather it describes, in a little more detail, what the spectrum of outcome effects is likely to be for any delivery method, rather like a DNA profile. Sufficient work was done to develop a template for reporting on course learning outcomes in a way that builds on existing requirements in our university for such reporting. The Course Learning Profile was drafted for two courses, but did not reach a stage where it could be used effectively by a teaching team or department. It is a subject for further development.
We conclude that fuller reporting has considerable potential for promoting better decision-making with respect to course delivery, particularly as traditional modes of delivery are increasingly challenged.
Other aspects
LUMOS had two extensions. One involved other Mathematical Science Departments in universities around the country, especially in the identification of the Learning Outcome Spectrum. The other extension sought to interest colleagues from other disciplines both in assisting our deliberations by providing a wider perspective on Learning Outcomes, and also by inviting them to attempt a similar exercise in their own discipline.
The project also sought the involvement of national and international colleagues interested in the questions we were exploring. We were lucky to be able to use the expertise of several international experts who visited the project, became involved in various trials and made critical contributions.
Summary
The three innovative methods of delivering undergraduate mathematics were all implemented (two more completely than the third). A full list of Learning Outcomes was collected and categorised. The observation instruments for these learning outcomes were developed completely for two categories of outcome, past trial stage for three further categories, and initial progress made on a further three. This work is continuing beyond the project in five research studies. The Course Learning Profile, by which the impact of course delivery can be seen, was developed to template stage.
The project extension to other Mathematical Science Departments was undertaken with respect to the learning outcomes and prompted interest from national colleagues in the results of the project, but no replica innovations took place. The project extension to other subjects, on the other hand, was so strong that it outgrew this project and is now a separately funded, on-going project. Another unexpected development was the high level of interest in the LUMOS project from international colleagues who have become involved in on-going work, developing observation instruments.
Overall, we conclude that there is a need, and an opportunity, to develop a wider variety of delivery styles in order to better develop the wide range of learning outcomes that lecturers and other stake-holders expect of undergraduates in the mathematical sciences.
| Recommendation 1
Mathematical science departments should develop a wider range of course delivery methods in order that a wider range of learning outcomes (beyond curriculum lists of content and skills) may be developed for students. |
Innovative delivery methods
Team-based learning mode
Team-Based Learning (TBL) methods were implemented by a large variety of lecturers, to a large variety of students, in a large variety of courses: in mathematics, mathematics education, and statistics; and at foundation, undergraduate and graduate levels. A complete description of these methods as applied to courses in the mathematical sciences is available in “How To” Guide #1: Implement team-based learning.
In all cases, the innovations elicited favourable reactions from most students, and from all lecturers. In all cases, where teaching allocations have allowed it, the lecturers have continued with the innovation, and/ or intend to continue it in the future.
The courses where TBL was trialled were:
- MATHS 91P: Foundation Mathematics 1 (one of the Tertiary Foundation Course (TFC) mathematics courses) (40 students) (Mirko Wojnowski).
- MATHS 202: Tutoring in Mathematics (25 students) (Julia Novak).
- MATHS 302: An Introduction to Mathematics Education (40 students) (Judy Paterson, Greg Oates, Bill Barton, Caroline Yoon).
- MATHS 326: Combinatorics (Jamie Sneddon, Dimitri Leemans).
- MATHS 761: Dynamical Systems (Claire Postlethwaite, Vivien Kirk).
- STATS 210: Statistical Theory (80-100 students) (Rachel Fewster).
Data gathered about the use of TBL was restricted to informal lecturer-solicited feedback and standard university student evaluations.  As a broad summary of feedback, all staff and about 90% of students were in favour or strongly in favour of TBL methods across all courses.
As a broad summary of feedback, all staff and about 90% of students were in favour or strongly in favour of TBL methods across all courses.
From the point of view of staff, the strong positive responses tended to refer to the way the Readiness Assessment Tests (RATs) resulted in much higher levels of pre-lecture preparation and attendance by students, and on the warm class environment engendered by regular group work. On the negative side, several staff mentioned the high level of preparation needed to set a course up for TBL.
From the point of view of students, there were both strong and negative responses to the amount of group work (numerically, the positive comments clearly outweighed the negative ones), and appreciation for marks rewarding pre-reading.
No grade comparisons were possible, as no course had TBL and non-TBL streams simultaneously. In MATHS 326 (the course using TBL for the longest time (five years)) staff teaching graduate courses reported a subjective feeling that students understand the work better than previously. Most students, but not all, felt that grades were higher in TBL courses.
Team-Based Learning (TBL) methods have been developed in many contexts and their effects wellresearched. The LUMOS Project showed that TBL can easily be adapted to undergraduate mathematics, and that it promotes both mathematical communication and individual reading and problem-solving outside of lectures or tutorials. Furthermore, it proves to be popular with students and lecturers alike.
| Recommendation 2
One or two Team-Based Learning style courses should be included in the list of offerings for undergraduate mathematics, preferably in such a way that all students take at least one such course. |
Intensive technology mode
The 100-level course MATHS 102 Functioning in Mathematics was selected as the course to attempt to implement intensive technology use. This was undertaken by successive staff members throughout the period of the LUMOS project. MATHS 102 is an entry course for students who have not completed Yr13 mathematics at secondary school to the required standard. It is an introduction to calculus. MATHS 102 is run as a single stream every semester (including the Summer Semester). Some elements of the trial also took place in MATHS 150, the standard first course for those majoring in mathematical subjects.
 Three different aspects of technology use were trialled. The first was the use of technology for administration of the course. Technology use is increasing in the administration of most university courses, for example MATHS 102 already had its own website, and was administered through the on-line platform universally used at the University of Auckland. During the period of LUMOS, this system was changed from CECIL to CANVAS—both systems were capable of making resources and lecture recordings available, communicating with students, recording marks, and receiving feedback. We explored adapting them for running quizzes (now common practice) and establishing chat groups. It is quite clear that these platforms will continue to develop and increase functionality as part of normal university processes. However, our use of the platforms to establish new uses (make them work, introduce the new uses to students, and train staff) confirmed that these are nontrivial tasks. Major systems of this kind require significant staff input and adaptation to make them useful.
Three different aspects of technology use were trialled. The first was the use of technology for administration of the course. Technology use is increasing in the administration of most university courses, for example MATHS 102 already had its own website, and was administered through the on-line platform universally used at the University of Auckland. During the period of LUMOS, this system was changed from CECIL to CANVAS—both systems were capable of making resources and lecture recordings available, communicating with students, recording marks, and receiving feedback. We explored adapting them for running quizzes (now common practice) and establishing chat groups. It is quite clear that these platforms will continue to develop and increase functionality as part of normal university processes. However, our use of the platforms to establish new uses (make them work, introduce the new uses to students, and train staff) confirmed that these are nontrivial tasks. Major systems of this kind require significant staff input and adaptation to make them useful.
The second aspect trialled was the use of computer laboratory-based tests. We were able to make this work, in a practical sense, for a course of 100+ students. However, it required a greater organisational load; and some students experienced difficulties that would have affected their test performance. The test preparation required greater lecturer input. We did not feel that this was worth the positive aspects: quicker marking and easier mark administration. Computer-based tests were not significantly different to supervise. The tests were less flexible pedagogically, that is, it was more difficult to have a variety of question styles or to test processes as compared with factual knowledge.
The third aspect of technology trialled was the use of computer software and internet connections during lectures by either or both of students and lecturers. Those students who owned and carried devices to lectures (about 50% in a survey conducted in the first year of the project) welcomed the freedom to use them, and did respond to in-lecture requests to find information or resources online in real time. A graduate student (Sarah Schinke) observed students in tutorials and found some evidence of deeper mathematical thinking associated with technology, but not sufficient to generalise beyond this course.
From the lecturers’ point of view, it is normal procedure to be able to access and display websites during lectures, so that aspect is not an innovation. What was attempted was the use of websites and tailormade software (Wolfram Alpha, GeoGebra and Desmos) to model technology use in the calculus section of the course, making use of dynamic visualisation. The students gave positive feedback on this initiative, and we found evidence for both increased technology use and positive attitudes towards technology. There was no evidence either for or against the initiative in the results of tests or examinations, but examination question responses showed effects related to the lecturer’s use of technology (see McMullen, Oates & Thomas, 2015). This research is on-going (see Thomas, Hong & Oates).
Initiatives of this latter kind are highly lecturerdependent. There is a significant investment in time required by the lecturer the first time such software is used (our experience was that a new technology about doubled preparation time for the first instantiation, and again when upgrades occur), so the lecturer needs to be convinced this is worthwhile and be motivated to use it.
Overall, we are in favour of continued increases in the use of technology, especially as a pedagogical tool by lecturers, to present more ways for students to access and understand course material—not just to do what is done now more efficiently. However, we believe that such moves will not succeed unless they are done at the lecturer’s pace and with regard to equity.
Low Lecture mode
The Low Lecture mode was undertaken as a voluntary extra stream of MATHS 108 General Mathematics 1. This is the largest course offered by the department, and runs in multiple streams every semester. This course is the standard entry course for those not intending to major in mathematical science subjects. It builds on secondary school calculus and is an introduction to linear algebra.
Three trials were undertaken (numbers in brackets indicate student volunteers completing the course in the trial stream): Semester 2, 2013 (14); Semester 1, 2014 (12); and Semester 2, 2015 (8). In each trial, about 4 students who initially began in the stream chose to return to the standard stream, in most cases due to timetable issues. Trial lecturers were Professor Bill Barton and Associate Professor Ben Martin.
The Low Lecture trial differed from standard delivery in two main ways: only offering one lecture per week and expecting students to study content and skills on their own; and offering Engagement Sessions in which semi-authentic mathematical activity was undertaken in small tutorial groups. A full description may be found in Appendix 3, which contains an edited version of the Information Sheet inviting students to participate in the trials. Note that the Low Lecture mode is not “Flipped Learning”. At the same time as LUMOS was being undertaken in the Department of Mathematics, another lecturer was trialling some “flipped lectures” with MATHS 208, the follow-on course for MATHS 108, with reportedly good results.
The Low Lecture trial compared data on two student groups: those taking the standard mode and those taking the Low Lecture mode. Volunteer numbers remained low, so there was likely an experimental effect that benefitted the trial students. However, this enabled us to collect significant personal data on motivations and evaluations of the Low Lecture mode. The comparison showed no significant differences on grades or any other measure of mathematical learning when adjusted for expected performance. There was a slight (but not significant) difference in favour of the Low Lecture mode on attitude.
What became clear from the trial was that the Low Lecture structure of one lecture and a reliance on self-initiated learning suited some students very well, but did not suit others. Those benefitting were: parttime students involved in work or child-care; students taking more than a standard load of courses; mature students; and highly organised or motivated students. It suited the first two categories because it meant that these students did not feel required to attend so many lectures. It suited those in the other three categories because they were already suited to the new learning culture. This mode did not suit students who were less well prepared and/or disorganised in their study habits.
The semi-authentic mathematical experiences were strongly liked by both lecturers and staff. The opportunity to be mathematically creative and to work mathematically closely with lecturers appealed to many students. Lecturers enjoyed the open-ended nature of the work and the challenge of handling tutorials that had no pre-determined content.
As a result of the trial we are convinced that it is possible to give students the opportunity to take more control of their own learning, and this would benefit a large section of students. We are not certain that the particular model we used is appropriate. However, elements of our model may prove useful starting points. See “How To” Guide #3: Shift responsibility for learning onto students.
The Low Lecture trial demonstrated that it is possible to significantly change the lecture delivery model, to increase student responsibility for learning, and to incorporate semi-authentic mathematical activity at undergraduate level—and that many students are likely to react positively to these changes. However, we are not convinced that the Low Lecture mode as trialled is the ideal vehicle for these initiatives. Rather each initiative could be introduced separately in appropriate courses. This would allow a gradual change of learning culture.
| Recommendation 3
Increasing student responsibility for learning while providing appropriate back-up should be an aim for initiatives in undergraduate courses. |
| Recommendation 4
Designing appropriate semi-authentic activities as part of core undergraduate mathematics courses should be a priority for all undergraduate programmes. |
Desired learning outcomes – The Spectrum
One of the first tasks of the LUMOS project was to survey undergraduate lecturers and other stakeholders on their desired outcomes for undergraduate degrees in the mathematical sciences. The information from interviews was combined with writing in the literature, university graduate outcome statements, and course descriptions.
Most of the information came from interviews. Twenty- five lecturers, mostly from the University of Auckland, but including lecturers from other NZ and overseas universities, were interviewed. They came from pure mathematics, applied mathematics, statistics, engineering science, and computer science disciplines.
The results were categorised and catalogued in the Learning Outcome Spectrum (see Appendix 1).
Several notable issues emerged from the interviews, in addition to a comprehensive set of learning outcomes.
First, even when pressed, very few of those we interviewed wanted to specify any particular content as absolutely necessary for any course or for a full mathematical degree. However, nearly all interviewees expressed strong views about mathematical processes or modes of behaviour that they regarded as essential for mathematical graduates. This result mirrored an earlier research project, where similar views were expressed (Barton, Clark, & Sheryn, 2010). The issue is summed up by one lecturer who said “I do not mind what mathematics they have learned; I just want them to have experienced what it is like to learn some mathematics in a deep way”.
Second, we expected that lecturers would want their students to increase their liking for mathematics as a result of taking undergraduate courses. In fact, not a single lecturer voluntarily mentioned this as a learning outcome, and, when asked explicitly, they responded that it was irrelevant (or, in a few cases, the students’ positive attitude to mathematics was assumed). However, many lecturers then expressed a different kind of attitude that they did value as an outcome. This attitude was variously expressed as “interest in”, “respect for”, “advocacy of”, or “appreciation of” mathematics. This strong difference in desired attitude compared with secondary teachers, for example), led to (a significant development in the observation instrument that was subsequently developed (see below).
Third, many lecturers speak about mathematical behaviours, such as when a student is faced with a problem. For example, lecturers want students to be able to break it down, to find the tools needed, to teach themselves some necessary mathematics. They also talk about the confidence to do these things. But noone mentions the desire to exhibit these behaviours. Students may be able to think mathematically, but surely we also hope that they will be motivated to behave this way.
Fourth, we were surprised by the frequency lecturers spoke about making errors, or not knowing. They universally saw these as positive events, and valued highly the ability of students to respond appropriately. Making errors or being ignorant of something, identifying the errors or areas of ignorance, and using this awareness usefully were seen as key behaviours and a necessary part of being mathematical.
Finally, despite the widespread recognition that a vital role for universities is to be a critic and conscience for society, no-one mentioned learning how to use mathematics ethically, or as a tool for social responsibility, as a desired outcome for a mathematical undergraduate.
Observing learning outcomes
The project sought to develop ways of observing whether or not the desired learning outcomes were being achieved. Creating, testing and validating observation instruments was seen as a significant step towards being able to link course delivery to student achievement.
The observation instruments needed to be easy to use, that is, ideally they should not require training to administer, nor be complex to analyse. They also needed to be very light on student and lecturer time. Most importantly, they had to be sensitive enough to distinguish growth in the desired learning outcome both between different courses, and also within a course between the start and the end.
The instruments did not need to measure individuals, only the growth of the learning outcome for the class as a whole. Of course, the instrument could be the sum of individual scores of all class members, but that was not required.
Mathematical achievement
During the project, we found no reason to believe that it was necessary to develop new measures of mathematical achievement, conceived as knowledge of the course content and related skills. The present regime of quizzes, tests, assignments, and examinations that is more or less common to all NZ mathematical science departments is more than adequate—and has been for a long time.
What has emerged, however, is that with very little further effort, a much finer-grained analysis is possible with the class data that already exists. Such a conclusion is not news. The rise of the discipline of learning analytics has argued for such use of data for some time across many disciplines. While small moves are being made in the mathematical sciences, these are often informal and ad hoc. In LUMOS, investigations into further use of existing data were led by Julia Novak. We recommend a stronger, more formal approach to this.
Past test and examination data is available for most courses stretching back many years. We also have increasing documentation concerning syllabus changes, student cohort changes, both school and university prior courses, and delivery changes (e.g. lecturers, timing, use of technology). End of semester examination meetings usually take note of very recent past courses as a means of validating present marks. A more rigorous analysis could uncover useful information about course delivery.
Generally, only past examination data is used to validate present marks. However, test data is also collected under examination conditions and often relates to parts of the syllabus not tested in examinations. Assignment data, while being less reliable as individual measures, relates to different sorts of knowledge, longer questions, and otherwise untested skills and behaviours. Comparing data from different assessment types can increase the range of learning outputs observed.
Longitudinal data is also available for students. For example, their grades (and component scores) are known for all previous courses taken in the department concerned. Grades are often compared for students taking several courses, however a regular and more comprehensive approach could do more than validate current results. For example, the impact of one course upon another as a pre- or co-requisite, or the transfer of knowledge from one type of course to another context, could be achieved.
Other possibilities exist for the use of learning analytics. For example, using data from within an examination, it may be possible to better understand how content affects the learning of skills, or vice versa. Similarly, cooperating departments could do cross-disciplinary analysis; or two of the three types of data could be combined, such as timeline analysis of links between test and examination marks. We do not regard the benefits of these other possibilities worth the effort at this stage, although learning analytics is a developing field, and we believe it can be exploited in the context of undergraduate mathematics.
| Recommendation 5
Learning analytics should become increasingly part of course reporting, not just for validating current marks, grades, or result profiles, but for reporting on the effectiveness of courses in achieving particular desired learning. |
The Course Learning Profile (see Appendix 2) includes minimum learning analytics data as standard.
Mathematical communication
For this category of learning outcome, we were fortunate to be able to draw on an extensive literature on mathematical communication at primary and secondary school level as a starting point. Existing models for observing both written communication and oral communication ended up being significantly adapted to meet the needs of the tertiary level.
The trials for observing written communication were based on finding appropriate types of questions and efficient but effective marking rubrics. The trials were conducted with 100-level courses. On several different occasions an assignment or a test was designed to include a question of the type: “Imagine that a friend missed a lecture on xxx. Write them an email explaining the idea of xxx.” Different versions at different levels of detail were tried. Different marking rubrics were also trialled.
The most successful results were obtained when the questions included some specific instructions on the type of explanation required, for example, that both symbols, graphs, and text should be used. Lacking this direction, student answers became so diverse that any meaningful evaluation of them was impossible. Responses improved if it was made clear to students that the purpose of the question was to evaluate communicative ability.
The main difficulty in marking responses was to separate the communicative quality from the mathematical correctness. However, this is achievable, and marking communicative questions was probably quicker than marking standard questions.
We noticed that the communicative questions had a strong positive effect on the students, and the standard of communication improved just because the questions were present. We also found the initial responses were generally much worse than we expected them to be, highlighting the need for some pedagogical emphasis in this area. We therefore strongly recommend the regular use of such questions in core undergraduate courses.
The trials for observing oral communication were more complex. They took place in both 100- and 200-level classes. We tried observing oral communication both in lectures and in tutorials. The former proved impractical due to the general low frequency of two-way communication. In tutorials, we found it necessary to specifically design the set-up of the tutorial questions to elicit student communication. Groups of three students were ideal.
Observing oral communication needed some training and practise. Thus, we did not achieve our aim of a simple, easy-to-use instrument. However, given a reasonable amount of experience working in tutorials, effective questions for the students to talk about, and two or three trials of using a recording rubric, a tutor or a lecturer can obtain results that will be robust and sensitive to observing change. The result of the observation is at a class level, not an individual level.
Subjective “gut feeling” proved to be generally reliable and correlated well with recorded observations, however there were observer differences. (“Gut-feeling” is a term used in the literature for what may otherwise be described as “experienced professional judgement”. See “How To” Guide #5: Monitor the development of mathematical communication for more information on such evaluations). We recommend combining “gut feeling” with explicit observations on a schedule. The increased staff investment needed for observing oral communication leads us to recommend limiting these observations.
Mathematical communication is an important characteristic for all undergraduates. We believe that this aspect should appear regularly in assessments, if for no other reason than to highlight its importance. Written communication can be observed with little effort so that courses that impact on student communicative ability can be seen. Oral communication is more difficult to observe effectively.
| Recommendation 6
Core undergraduate courses should include a question that elicits communicative ability in most tests and assignments. |
| Recommendation 7
At least two core undergraduate courses should be designed so that oral communication can be observed in tutorials by a small group of suitably trained tutors using a tested schedule combined with “gut feeling” measures. |
Affective outcomes
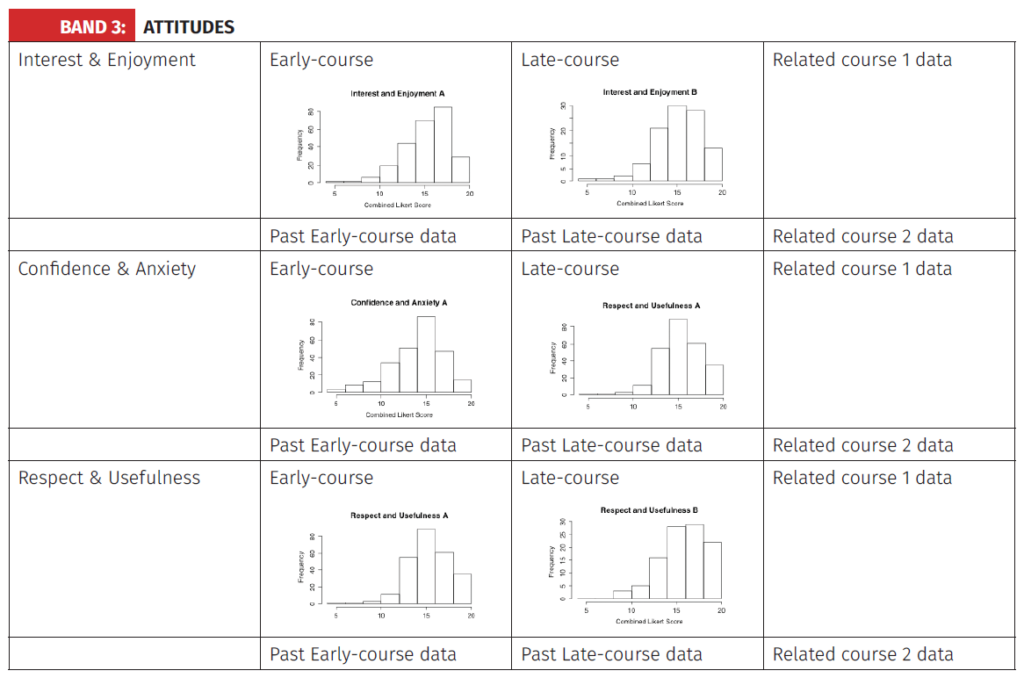
As for mathematical communication, so too were we able to draw on the literature on mathematical beliefs and attitudes. In particular, Cretchley (2012), had already designed and statistically validated a questionnaire that measured three affective dimensions of mathematical belief at tertiary level.
We were not interested in the technology-related beliefs, which were one of Cretchley’s dimensions, however we were interested in capturing another type of belief that lecturers had described in the interviews as a desired affective outcome, namely the respect for, and appreciation of, mathematics. Our work, therefore, concentrated on validating Cretchley’s other two dimensions (confidence & anxiety, and interest & enjoyment) and designing questions that would capture this other aspect (which we named respect & usefulness). See “How To” Guide #4: Monitor feelings and beliefs about the mathematical sciences for samples of the instrument).
It was then necessary to undertake statistical analysis to establish whether this new dimension was independent of the existing two. We also wanted to be sure that the resulting questionnaire was reliable and sensitive enough to detect changes in attitudes between courses and between the start and end of a single course.
The statistical analysis was undertaken by Liza Bolton, then an undergraduate student in statistics, on a Summer Scholarship and subsequently on a paid basis.
Four courses were the target of several trials: MATHS 102, MATHS 108, MATHS 208, ENGSCI 111. While the syllabus of these courses is similar (all courses cover calculus and linear algebra topics), they are at different levels and attract different cohorts of students. MATHS 102, 108, 208 follow-on from each other. ENGSCI 111, as the entry level engineering course, has a betterprepared cohort mathematically.
The 12-question, 2-minute questionnaire was trialled as both on-line and paper administration, and both in class and in students’ own time. The on-line/own time administration attracted the lowest response rate. The on-line/in class form of administration was most efficient and obtained a sufficiently high response rate.
 We obtained sufficient data to have significant statistical results. The third dimension did indeed prove to be independent of the other two (after adjusting a couple of the questions). Furthermore, we were able to show that the questionnaire both distinguished between courses, and showed changes in individual dimensions over a single semester. For example, we discovered that MATHS 108 students were less confident than MATHS 102 students, despite the fact that the MATHS 108 cohort had been successful at Yr 13, whereas the MATHS 102 cohort were not. This led to changes in our teaching to enhance students’ confidence when we had previously not thought it was needed.
We obtained sufficient data to have significant statistical results. The third dimension did indeed prove to be independent of the other two (after adjusting a couple of the questions). Furthermore, we were able to show that the questionnaire both distinguished between courses, and showed changes in individual dimensions over a single semester. For example, we discovered that MATHS 108 students were less confident than MATHS 102 students, despite the fact that the MATHS 108 cohort had been successful at Yr 13, whereas the MATHS 102 cohort were not. This led to changes in our teaching to enhance students’ confidence when we had previously not thought it was needed.
Note that the instrument was not tested for its reliability for individual assessment of attitudes, it is only validated as a measure of the whole class. Thus, anonymous administration is recommended.
Since the questionnaire gives such good results, is easy to administer, and occupies very little lecturer or staff time, we recommend its use at least once at each year level of an undergraduate course, and occasionally in every course in order to evaluate the effect of that course on attitudes.
| Recommendation 8
Monitoring attitudes at least once at each year level of an undergraduate course, and occasionally in every course to evaluate the effect of that course on attitudes should be a standard part of an undergraduate programme. |
Conceptual learning
When the project began, we intended to follow the emphasis in the literature and explore ways to observe conceptual learning of mathematics. We changed focus during the project, partly because the field was so broad, partly because conceptual learning appropriate for a particular course is partially observed in standard examinations and assignments, and partly because we found it difficult to define this characteristic in a useful way that captured the variations in what lecturers described under that heading.
As a result, the lead researcher for this part of the project, Associate Professor Caroline Yoon (assisted by two students, John Moala and Benjamin Davies), turned her attention to the idea of conceptual readiness. Conceptual Readiness refers to the understandings that a student needs to have in order to properly receive the ideas that a course is about to deliver. Observing conceptual readiness relates to the process of checking whether students have the pre-requisite knowledge for a course, but focuses on deeper understanding rather than factual knowledge or specific skills.
The first problem was to find a way to elicit conceptual readiness. The team worked on creating tasks that could be worked on in tutorials, and would create a situation where the student work would not rely so much on content knowledge or specific skills, but rather on thinking through the problem using their mathematical understanding.
Building on earlier work at secondary school level designing mathematics eliciting activities (MEAs), Caroline Yoon and her team first established a set of criteria for conceptual readiness tasks. The key idea is that the task should result in students getting stuck (but not giving up) and thereby forcing deeper mathematical thinking.
Trials were held in a 300-level combinatorics class, and with three groups of first year volunteer students working on the preliminary conceptual understanding of induction. The trials both resulted in the generation of evidence of conceptual readiness, although in both cases the time required was more than one session. In the combinatorics trial, there was significant evidence that the students were better prepared for later formal presentation of the concepts. That is, the process of trying to observe conceptual readiness appeared to perform a pedagogical function as well.
We recommend continued research in this area. Caroline Yoon is continuing her work in this area beyond the LUMOS project.
Mathematical habits
Our catalogue of desired learning outcomes contains an extensive list of mathematical habits (as opposed to general learning habits that apply across disciplines). We attempted to develop observation instruments for several of these.
Our attempts ran into a series of difficulties that occurred with each habit. They were:
- defining or describing the habit accurately enough;
- the relative rarity of instances of each habit, especially at an individual level; and
- the dependence of performance on mathematical content knowledge.
Not only do most habits have many different components, or are described differently by different lecturers, but also, for the purposes of developing an observation instrument, the different stages in the development of a habit needs to be described. This is further complicated by the unsurprising discovery that development is not usually linear through universal stages.
The way that undergraduate courses focus primarily on content and skills, particularly at lower levels, made it very difficult for us to find instances of any particular habit. Sufficient repeated instances were not observable at the individual level, although in some cases we found enough instances taken across a whole class—usually only if we induced the behaviour in some way.
Most habits develop in conjunction with increased mathematical content knowledge and routine skills. Thus, separating the formation of habits from knowledge is not always easy.
A final point to be noted: as for Mathematical Communication and Conceptual Readiness, explicit attention to a mathematical habit had a pedagogical effect in promoting that habit. This in itself may be sufficient reason to pursue further work in this area.
Our various trials did not result in fully-developed instruments, but we did develop several generic techniques for overcoming the problems mentioned above. These are described in the “How To” Guide #7: Develop mathematical habits.
Persistence
A suitable definition was the first task for the group working on the habit of persistence. The diagram below was developed after discussion and consulting the literature.
Our trial took place with a 100-level class, using a questionnaire that was attached to an assignment. Our trial identified three problems. First, we found that persistence became conflated with its context (some form of problem-solving). Second, student responses to different questions were sometimes contradictory, and were always very context dependent. Finally, persistence does not imply continuous work on a problem, thus the time scale can be very different for different instances of persistence.
We trialled revised versions of the questionnaire, and made some progress, but do not have a final model that we are confident is suitable for general use.
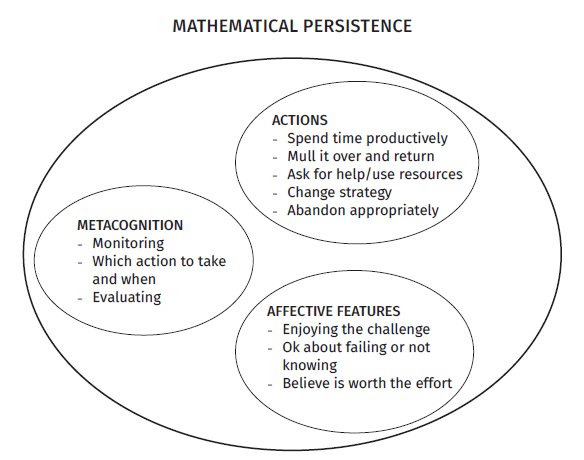
Figure 1: A Model of the components of Mathematical Persistence
Mathematical Foresight
One habit that was not mentioned by lecturers in the initial interviews, but was identified by a LUMOS researcher, Wes Maciejewski, and then confirmed as important in a subsequent round of interviews with mathematicians. This is the habit of Mathematical Foresight. It refers to the ability to conceive of the resolution of a problem or proof, and the broad, likely pathway to the resolution. It includes the recognition of whether a problem is solvable with present knowledge. A full description is available in Maciejewski & Barton, (2016).
We attempted to design tasks that would elicit mathematical foresight and a marking scheme for the student responses. We trialled them with a class of 300-level students.
The responses proved difficult to mark; however, it became apparent that the problem was with the tasks and not the marking scheme. Some adapted tasks were tried, but we remain unsatisfied that we have models that are suitable for general use.
Hypothesising, generalising and abstracting
Professors Bill Barton and Arkadii Slinko from the University of Auckland combined with an international group of lecturers to discuss how to elicit hypothesising, generalising and abstracting behaviours. The international group were Professor Chris Sangwin (now at Edinburgh University), Dr Matthew Inglis (Loughborough University), and Associate Professor Kevin McLeod (Wisconsin Maddison University). Taking inspiration from the work of Al Cuoco (see Cuoco, Goldenburg, and Mark, 1996), and starting from the automated system design by Chris Sangwin and the Comparative Judgement techniques of Matthew Inglis, we discussed possible questions and delivery techniques to observe these habits.
One idea we explored was to adapt the idea of a concept inventory to mathematical processes. Concept inventories exist in the mathematics education literature, particularly around algebra. We used ideas from Polya (2014) and Mason (2010) and attempted to construct a problem that required a series of calculations from which students would attempt to identify patterns (generalisation). A rubric was found that asked students to note down when they were stuck, when they had an idea, when and how they checked their idea, and a summary of their work.
Unfortunately, we did not get to the stage of significant trialling of the problems we collected.
Mathematical versatility
Professor Mike Thomas continued working with his initial conceptualisation of versatile thinking, working with Ye Yoon Hong (see Hong & Thomas, 2014). They used this work while teaching calculus. In addition, Mike Thomas developed tutorial tasks for the calculus section of MATHS 102 that elicited versatile thinking in conjunction with his work on technology (see Intensive Technology Mode on page 9). This research is on-going (Thomas, Hong, & Oates).
Other habits
Other mathematical habits that appear in our inventory, but for which we did not try to develop observation instruments, include: strategic thinking; experimentation; defining; objectifying; and conjecturing.
Problem-solving, proving, creativity, and modelling
As well as distinctly mathematical habits, there is another set of broader processes that appeared in the desired learning outcome catalogue. The four main ones all have an extensive literature and many published and tested means of eliciting or observing them exist. We did not initiate any major work with any of these four processes except modelling.

The modelling group included two LUMOS researchers, an applied mathematician and a statistician from Auckland, a sabbatical visitor, Dr Brynja Kohler (Utah State University), and Dr Andrea Bruder (Colorado College). We held a series of discussions and decided to interview applied lecturers in the mathematical sciences to better understand exactly what mathematical modelling attributes were desired in undergraduates. The overall description was labelled “sophisticated modelling” to distinguish it from practicing modelling or decontextualized modelling that often occurs during secondary school and undergraduate courses.
An interview protocol was designed and some characteristics of sophisticated modelling identified:
- whether students fit data to a model (more naïve) or model to the data (more sophisticated);
- whether students have a modelling aesthetic, that is do they think models are right or wrong (more naïve), or think they are better or worse (less naïve), or think they are fit for purpose (more sophisticated);
- whether students have fluency between the mathematics and the phenomenon under consideration;
- what is the student’s awareness of available mathematics: do they only consider mathematics they know (naïve), or wonder who knows or where to find the mathematics they need (less naïve), or think about what (possibly new) mathematics is needed (more sophisticated)?
Further interviews took place with a group of graduate students in applied mathematics. As well as confirming the above, the group suggested the ability to make the model generic as a further characteristic of sophisticated modelling.
This work needs to become part of the international conversation on modelling to proceed further, there is little point in working in isolation when many others are interested. Such work was not part of LUMOS.
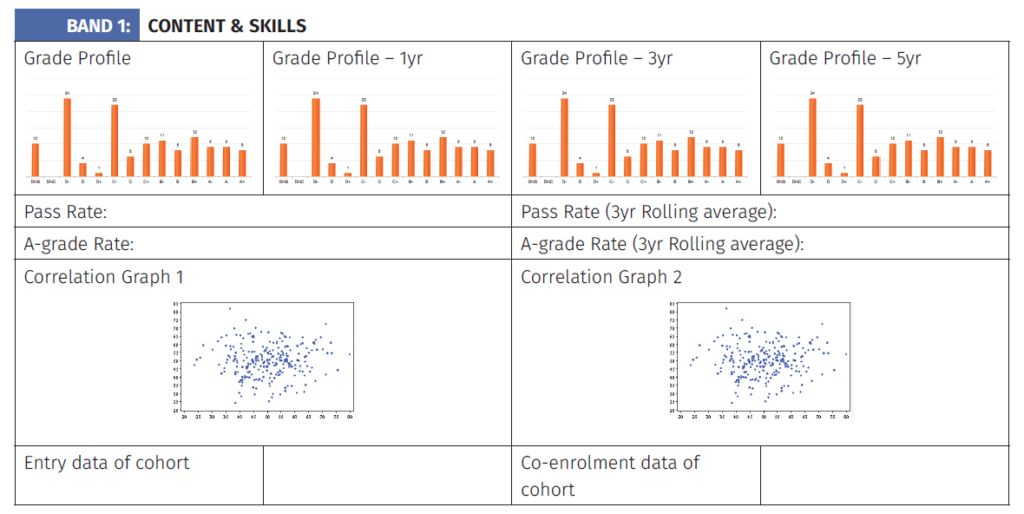
Course learning profileMost universities have templates for recording course data and syllabus or teaching changes over time. The Course Learning Profile (CLP) was intended to be an additional document that would report on the desired learning outcomes identified in the first part of the LUMOS project. It would not replace or supersede any existing documents.The CLP was designed to consist of separate bands, each band reporting on one (or one type of) learning outcome for which an effective observation instrument was available. It remains a work in progress. As further observation instruments are validated in our on-going research, more bands will be added. It is not envisaged that the CLP will be completed in full for every course, every time it is delivered. Rather the CLP is intended to provide a reminder of learning outcomes that are sometimes ignored, and provide a template for any lecturer who wishes to try to record observations of those outcomes. We expect that it will be adapted by each lecturer to fit their context and whatever observation instrument they use. At this stage the CLP consists of six bands: Content & Skills; Mathematical Communication; Attitudes; Conceptual Readiness, Mathematical Habits; and Mathematical Processes. Both the last two bands are made up of sub-bands. The set of sub-bands remains incomplete. Not included in the CLP at present are the broader generic learning habits such as Collaborating or Critical Thinking. The Content & Skills band, as well as a Mark Profile and Pass and A-grade rates, includes historical rolling average data and past profiles of 1, 3 and 5 years ago. It also includes correlation graphs for one or two prior courses. Optional data is any information on the entry standard of the student cohort, and co-enrolment information. The Mathematical Communication band contains sub-bands for written and oral communication. In both cases the data to be collected includes both early- and late-course observations. The Attitudes band contains early- and late-course survey data. Optional data is comparisons with other related courses, and averaged historical data. The Mathematical Habits band is incomplete. Existing sub-bands for Mathematical Persistence, Mathematical Foresight, Versatile Thinking, and Hypothesising are included, with space for others to be added. Similarly, for the Mathematical Processes band, we have included Proving and Modelling, and expect more to be added later. Each band (or sub-band) has a colour-coded square on a five-shade scale giving the overall assessment of the learning outcomes compared with previous or expected outcomes. See Appendix 1 for the current template. |
Project extensionsAdvisory groupsThe project consulted three advisory groups. The University of Auckland and the National Advisory Groups each met twice as a collective, but all members were consulted on at least one, and in some cases, two or three occasions. The International Advisory Group all visited Auckland at least once during the project, and three members visited twice. In particular, three members of the international group participated in one or more Engagement Sessions in the Low Lecture Mode trials, and gave valuable insights from a broader perspective. The University of Auckland Advisory Group consisted of: Professor Helen Sword from the Centre for Learning and Research in Higher Education; Associate Professor Rachel Fewster from Statistics; Dr Peter Bier from Engineering Science; and Dr Julia Novak and Dr Steven Galbraith from the Department of Mathematics. The National Advisory Group consisted of: Associate Professor Megan Clark of Victoria University; Dr John Hannah of Canterbury University; and Professor Glenda Anthony of Massey University. The International Advisory Group consisted of: Dr Elena Nardi, University of East Anglia; Professor Barbara Jaworski, Loughborough University; Professor Celia Hoyles, University of London; Professor Michèle Artigue, Université Paris VII; and Professor John Mason, Oxford University. Several other international visitors to the Department showed interest in the project and participated in aspects of it. Associate Professor Kevin McLeod from Wisconsin-Maddison, Professor Chris Sangwin from Edinburgh, and Dr Brynja Kohler from Utah State University in particular gave willingly of their time to the project. Other mathematics departmentsThe Schools of Mathematics and Statistics at both Victoria University and Canterbury University were invited to participate in the LUMOS project, particularly with the first phase of identifying desired learning outcomes. Associate Professor Megan Clark and Dr Steven Archer from Victoria, and Dr John Hannah and Associate Professor Alex James from Canterbury were our contacts. Three meetings of this group were held, both in Auckland, and at the NZ Mathematics Colloquia held in the project years where all were present. The two universities participated, as planned, in the initial interviewing process and cataloguing of the desired learning outcomes. They were kept in touch with later parts of the project as they evolved, and each one participated in an advisory capacity in at least one other component. In addition, they gave feedback as we reported progress throughout the project. We would like to record the project teams’ thanks for their useful comments and willing participation. Other subjectsA group of representatives from other departments of the University of Auckland formed a group that also met in the initial stages of the project. The intention was to get better generalisation of any results of the project by keeping in mind differences between disciplines, and also to get an outsider perspective on the project. The group members were: Professor Helen Sword and Dr Barbara Kensington-Miller from the Centre for Learning And Research (CLeAR); Dr Alys Longley, Dance Department; Dr Alison Cleland, Faculty of Law; Associate Professor Nikki Harré, Department of Psychlogy; and Dr Shaun Sterm (then English Department, now CLeAR). This group contributed strongly in the early stages, for example, our meetings at that time debated at length about the categories of learning outcomes that would be useful. The group also found much to interest them in the project, and eventually they formed an independent group that applied for, and received, its own funding to adapt the LUMOS project to their own subject areas. |
Conclusions
Lessons learned
Both parts of the project, developing innovative delivery methods and observing learning outcomes, have given us lessons for future work.
 The main lesson to come from the innovative delivery development is that changing delivery methods, even quite drastically, has little effect on traditional content and skills outcomes as conventionally measured. That is, given contact with staff, support mechanisms, and information about the curriculum, students seem to achieve content and skills objectives, as measured by examinations, at the levels they have always reached. There is thus no reason to discontinue experimenting with aspects of delivery like student responsibility for learning, use of online resources, use of lectures, alternative assessments, or group work. We are encouraged to continue to use evaluations, educational literature, and an open mind to propose and test modifications to courses, and evaluate them against student learning.
The main lesson to come from the innovative delivery development is that changing delivery methods, even quite drastically, has little effect on traditional content and skills outcomes as conventionally measured. That is, given contact with staff, support mechanisms, and information about the curriculum, students seem to achieve content and skills objectives, as measured by examinations, at the levels they have always reached. There is thus no reason to discontinue experimenting with aspects of delivery like student responsibility for learning, use of online resources, use of lectures, alternative assessments, or group work. We are encouraged to continue to use evaluations, educational literature, and an open mind to propose and test modifications to courses, and evaluate them against student learning.
Each of the innovations has taught us (or re-taught us) important lessons. The Team-Based Learning innovation has affirmed the value of pre-lecture reading or problemsolving by students, and shown us a way to ensure the work is done. It has also affirmed that students are not averse to, and come to appreciate, group interactions— including second language English speakers. The element of individual assessment provided by TBL has the advantage of adding individual accountability, an advantage over other forms of group learning.
The Technology Intensive innovation re-taught us not to underestimate the difficulty of implementing technology in undergraduate education, despite the obvious educational gains of access to a wider understanding and efficient course administration. This study demonstrated the benefits of online-driven assessment and found evidence of improved versatility of students in the ways they can represent mathematical ideas. However, the issues of class-wide, permanent access to appropriate and reliable devices, and the time needed to gain easy familiarity with changing and diverse software and hardware remain significant barriers for both staff and students. A further issue in the immediate future is the attitude of both students and lecturers towards technology use, including a lack of awareness of the pedagogical value of technology as opposed to its use as a delivery and calculation tool.
The Low Lecture innovation had two significant components: handing back responsibility for learning to students; and introducing semi-authentic mathematical activity. The trials taught us that both are achievable in large undergraduate classes, at least to a limited extent. Our trials only involved classes of up to 20 students, but we are confident that they could be done with existing resources for classes up to 50 or 60. However, our recommendation is to introduce aspects of the Low Lecture Innovation, not the full trial—this could be done effectively with any class using existing resources. See “How To” Guide #2: Implement semi-authentic mathematical experiences and “How To” Guide #3: Shift responsibility for learning onto students for details.
Handing back responsibility requires a change of learning culture that some students find easier than others. Offering semi-authentic mathematical activities is heavy on lecturer time both for guidance and feedback, but has strong positive effects on students’ mathematical orientation. Another lesson from this innovation is that suitably supported flexible delivery, that requires less student time attending university, is possible for some students without a drop-off in grades.
Observing learning outcomes has also been very instructive to those of us who have been involved in undergraduate education for many years. The overall lesson is that many strongly desired, and expected, learning outcomes are not observed in any way, nor are they part of the design of course delivery. Nevertheless, we learned that some of them at least can be effectively observed in reliable ways, and could be used as part of course design.
Given that students choose what courses to take at university, we might expect that the affective outcomes of our courses would be of interest to lecturers, especially as we learned that they are very easy to observe. Given that employers want graduates who can communicate effectively and work in teams, then we might expect that mathematical communication would also be important, especially as it too can be observed with a modicum of preparation.
We have learned that mathematical habits such as hypothesising, proving, persisting, knowing where to turn for help, or making links across the discipline, are strongly valued by lecturers at the upper levels of undergraduate education, but are not (except for proving) addressed explicitly. We believe that effective tools to observe the evolution of these learning outcomes may well prompt developments in course delivery that will assist students acquire such habits. We have learned that creating such tools may be more difficult than we initially anticipated.
The major research lesson we learned was the opening up of the topic of educational assessment that occurs when the focus of evaluation is the whole class rather than individuals. Not only does this perspective allow the evaluation of interactions between students, and between staff and students, but also it opens new techniques for observation and analysis. A third benefit of this approach is that it allows us to evaluate characteristics which have very low frequency of occurrence for any individual, but may have sufficiently high occurrence for a class. We believe that we have added significantly to research methodology in this area.
A theoretical contribution of note was the work done in the Intensive Technology mode where technology use was examined from the perspective of orchestrations.
Conclusions and recommendationsRecommendation 1 With respect to course delivery innovation, we conclude that there is a need, and an opportunity, to develop a wider variety of delivery styles in order to better develop the wide range of learning outcomes that lecturers and other stake-holders expect of undergraduates in the mathematical sciences. Recommendation 2 Team-Based Learning (TBL) methods have been developed in many contexts and their effects well researched. The LUMOS Project showed that TBL can easily be adapted to undergraduate mathematics, and that it promotes both mathematical communication and individual reading and problem-solving outside of lectures or tutorials. Furthermore, it proves to be popular with students and lecturers alike. The Intensive Technology trial affirmed the potential of technology to transform mathematics teaching and learning at this level, but also demonstrated the input required to make this happen at the course level, even if they are “proven” systems adopted by the university. Pedagogical gains will be gradual and the barriers to implementation remain significant, especially the need to change student learning culture. Equity remains an unresolved issue. We have no recommendations to make, as we believe that each department needs to proceed at its own pace within its personal and financial resources. Recommendation 3 Recommendation 4 The Low Lecture trial demonstrated that it is possible to significantly change the lecture delivery model, to increase student responsibility for learning, and to incorporate semi-authentic mathematical activity at undergraduate level—and that many students are likely to react positively to these changes. However, we are not convinced that the Low Lecture mode as trialled is the ideal vehicle for these initiatives. Rather each initiative could be introduced separately in appropriate courses. This would allow a gradual change of learning culture. Recommendation 5 Our project revealed several opportunities for using data that is already widely gathered through tests and examinations. Learning analytics is a developing field, and we believe it can be exploited in the context of undergraduate mathematics. Recommendation 6 Recommendation 7 Mathematical communication is an important characteristic for all undergraduates. We believe that this aspect should appear regularly in assessments, if for no other reason than to highlight its importance. Written communication can be observed with little effort so that courses that impact on student communicative ability can be seen. Oral communication is more difficult to observe effectively. Recommendation 8 Attitudes are an important component of undergraduate education, and an effective, easy to use, non-time-consuming instrument to measure attitudes at the class level exists. We believe that monitoring attitudes at each level should be routine. Recommendation 9 Conceptual readiness is an important component of pre-requisite knowledge for undergraduate courses at all levels. Our project found that the process of generating student work that would enable us to observe conceptual readiness, also performed a pedagogical function to enhance students’ readiness. We therefore recommend further work be undertaken in this area with a view to assisting lecturers design appropriate preliminary tasks for students enrolled in their courses. Recommendation 10 Lecturers recognise, and value the learning of, a wide variety of mathematical habits. Several barriers exist to the development of the means to observe these habits. Further outputsAs a result of the LUMOS project, we feel that we have gained sufficient experience to provide guidance to others who may be considering course development in the mathematical sciences at undergraduate level. The following “How to” Guides are available.
Two further documents are available for those teaching undergraduates in the mathematical sciences. The first is the Catalogue of Desired Learning Outcomes (see Appendix 1), and the second is the draft Course Learning Profile Template (see Appendix 2). |
Appendix 1
Catalogue of desired learning outcomes
Catalogue of desired learning outcomes for undergraduate mathematics
CONTENT
| Knowing “That”
Mathematics understood in isolation as particular items, in such a way that material can be reproduced. E.g. Can you write down the Chain Rule for differentiation. |
Deeper Understanding
Topics understood in relation to other topics and within mathematics as a whole in such a way that material may be modified, used in unfamiliar contexts, and discussed in the abstract. E.g. Can you describe when it might be necessary to use the Chain Rule when trying to maximize a function. |
SKILLS / HABITS / PROCESSES / ATTRIBUTES
| Skills
Routine skills necessary to function mathematically, but developed in isolation. E.g. Use the Chain Rule to differentiate |
Habits
Distinctly mathematical habits that are necessary for successful mathematical work. See below for a more complete list of mathematical habits. E.g. Differentiate (recognition of need for the Chain Rule required) |
Processes
Higher level processes that are mathematical and involve the use of several skills. See below for a more complete list of mathematical processes |
Attributes
General attributes that are expected of academically competent students in all fields, including mathematics.
|
AFFECT
| Interest & Enjoyment Positive feelings towards mathematics which are independent of one’s competence. |
Confidence & Anxiety Self-assessment of ability in mathematics, and associated feelings. |
Respect & Usefulness Beliefs about the utility and pervasiveness of mathematics. |
Other Beliefs For example, beliefs about mathematics learning and teaching, or the philosophical nature of mathematics. |
More complete list of mathematical habits and processes
MATHEMATICAL HABITS
| Category | Habits | Sub-habits |
| Mathematical Meta-habits | Reasoning | Analysing and synthesizing
Logical thinking |
| Abstracting | Objectifying | |
| Generalising | Identifying: … patterns … key elements … structure … variance and invariance … assumptions … limitations and boundary conditions |
|
| Versatile Thinking | Representational fluency | |
| Developing a Tool-box | ||
| Argumentation | Testing | Finding examples and counterexamples |
| Justifying & Convincing | Arguing | |
| Mathematical Habits | Foresight | |
| Problem formulation | ||
| Conjecturing & Hypothesising | ||
| Symbolising | ||
| Defining | Refining definitions Exploring consequences |
|
| Mathematical Working Habits | Finding a suitable problem | |
| Playing Exploring Experimenting |
||
| Persisting Perseverance “Sustained niggling” |
… and knowing when to stop. | |
| Checking | Approximating | |
| Using mistakes |
MATHEMATICAL PROCESSES
| Processes | Sub-Processes | |
| Conceptual Readiness | ||
| Mathematical Communication | Understanding conventions Reading mathematics Writing mathematics Speaking mathematics Symbolic fluency |
|
| Problem-solving | Strategic thinking | |
| Proving | ||
| Mathematical Creativity | ||
| Modelling |
Appendix 2
Course learning profile template
Course learning profile for undergraduate courses in the mathematical sciences


Appendix 3
Low Lecture information sheet used to inform students about the trial (Edited)
The “Low Lecture” innovation has undergone its third trial in MATHS 108 in Semester 2, 2015. An extra stream of MATHS 108 will be created, and students who wish to take MATHS 108 in this delivery mode will volunteer for this stream. The first 30 students volunteering will be accepted into the stream.
The Low Lecture innovation will have only one lecture and one tutorial per week. (This differs from the conventional 3-lecture/1-tutorial/4-assignment design). The new learning will be Engagement Sessions. For these sessions (every 3 weeks, a total of three) students will be given an open-ended problem and asked to spend at least two hours investigating it (using the web and friends if they wish). They will then attend, in groups of eight with a lecturer, a 90-minute session in which two students will first be asked to present the work they have done. Then the whole group will work together (including the lecturer) to make further progress on the mathematical ideas that have been generated. Finally, students will individually write up their individual and group work, and submit this for marking. The marks for Engagement Session reports will replace the three assignments of the conventional course. Mark distributions for assignments in the conventional streams and Engagement Session reports in the innovation stream will be made equivalent through scaling.
All other assessments will be identical for Conventional streams and the Low Lecture stream, i.e. quizzes, tests, tutorials, examination. The Low Lecture stream will have its own tutorial, although (if necessary due to timetable constraints) students may attend other tutorials.
The single lecture in the Innovation stream will give overviews of the material and its significance, and will add historical notes, applications, links to other mathematics. The content and skills of the curriculum will be learned by students working independently in their own time, and will not be presented in lectures. Students will be directed to appropriate written and web-based resources for their work. On-line self-monitoring tests will be available to assess whether the material has been learned properly. Students’ participation in these tests will be monitored (but marks in these tests will not be part of the course assessment). Students not taking these tests or not reaching minimum standards will be offered assistance in organising their learning and/or understanding the material through extended office hours with the course lecturer or through other usual Department of Mathematics support systems.
While we expect students in the Conventional streams to attend only the conventional lectures, and students in the Innovation stream to attend only the innovation lectures, in fact all lectures will be open to all students, of either stream, (provided there is room in the lecture theatres). Likewise, all materials offered through the online learning management system to either stream will be accessible to all students. Conventional stream students will not have the Engagement Sessions (they will have access to the problems), but they will be able to use the self-learning resources and on-line self-monitoring tests.
References
Barton, B., Clark, M., & Sheryn, L. (2010) Collective Dreaming: A School University Interface, New Zealand Mathematics Journal 40, 15-31
Cuoco, A., Goldenberg, P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior, 15, 375–402
Cretchley, P. (2012). Students meeting Professional Mathematical Software: A Study of First-Year University Mathematics Learning. PhD thesis, University of Queensland.
Hong, Y. Y., & Thomas, M. O. J. (2014). Graphical construction of a local perspective on differentiation and integration. Mathematics Education Research Journal. 27, 183-200. DOI: 10.1007/s13394-014-0135-6
Maciejewski, W. & Barton, B. (2016). A Framework for Students’ Mathematical Foresight. Presentation at ICME 13, Hamburg.
Mason, J., Burton, L. & Stacey, K. (2010). Thinking Mathematically. Pearson
McMullen, S., Oates, G., & Thomas, M. O. J. (2015). An integrated technology course at university: Orchestration and mediation. In K. Beswick, T. Muir & J. Wells (Eds.) Proceedings of the 39th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 249-256). Hobart, Australia: IGPME.
Oates, G., Sheryn, L., & Thomas, M. O. J. (2014). Technology-active student engagement in an undergraduate mathematics course. In P. Liljedahl, C. Nicol, S. Oesterle & D. Allan (Eds.) Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 329-336). Vancouver, Canada: IGPME.
Polya, G. (2014). How to Solve It: A new aspect of mathematical method. Princeton Science Library.
Thomas, M. O. J., Hong, Y. Y., & Oates, G. (In press 2017) Innovative uses of digital technology in undergraduate mathematics. In E. Faggiano, A. Montone, & F. Ferrara (Eds.) Innovation and technology enhancing mathematics education. New York: Springer.
Project Outputs
Refereed Articles
Barton, B. & Paterson, J. (2013). Capturing Undergraduate Learning. CULMS Newsletter No.7., pp3-6.
Barton, B. (2014). Learning in Undergraduate Mathematics: The Trial of a Delivery Innovation. Mathematics Education Research Group Australasia Conference Proceedings.
Hannah, J., James, A. & Williams, P. (2014). Does formative assessment improve learning outcomes? International Journal for Mathematical Education in Science & Technology, 45(2), 269-281.
Maciejewski, W. & Barton, B. (2016). Mathematical Foresight: Towards a description. For The Learning of Mathematics
Novak, J. & Evans, T. (2013) Assessing students using multi-choice tests and exams: How to examine skills, processes and in-depth mathematical understanding. In D. King, B. Loch, & L. Rylands (Eds) Proceedings of Lighthouse DELTA, p246.
Oates, G., Sheryn, L, & Thomas M.O.J. (2013). In D. King, B. Loch, & L. Rylands (Eds) Proceedings of Lighthouse DELTA, p247.
Oates, G., Thomas, M.O.J., & Sheryn, L. (2014). Technology active student engagement in an undergraduate mathematics course. In Liljedahl, P., Nicol, C., Oesterle, S., & Allan, D. Proceedings of PME 38 p329-336.
Paterson, J. & Barton, B. (2013). Undergraduate mathematics outcomes: The mantis shrimp spectrum. In D. King, B. Loch, & L. Rylands (Eds) Proceedings of Lighthouse DELTA, p141-149.
Schoenfeld, A., Thomas, M.O.J., Barton, B., & Paterson, J. (2016). On understanding and improving the teaching of university mathematics. International Journal of STEM Education.
Yoon, C., Oates, G., & Sneddon, J. (2014). Undergraduate mathematics students’ reasons for attending live lectures when recordings are available. International Journal for Mathematical Education in Science & Technology, 45(2), 227-240.
Other major presentations include:
University of East Anglia, UK, Departments of Mathematics and Education, May 2013
Pacific Rim Conference, Plenary presentation, Sapporo, Japan, Jul 2013
University of Auckland, Department of Mathematics, Nov 2012
University of Auckland, Teaching Showcase, Jun 2014
UK Institute of Mathematics and Its Applications conference, Plenary presentation, Glasgow, Jun 2015
Norwegian Mathematics Education conference, Kirkeness, Plenary presentation, Oct 2015
Loughborough University, UK, Education Seminar, Oct 2015
University of British Columbia, Canada, Department of Mathematics, Nov 2015
NZ Australia Joint Mathematics colloquium, Melbourne, Dec 2015
13th International Congress on Mathematics Education, Hamburg, Plenary and one other presentation, Aug 2016
Acknowledgement
This work was supported through the Teaching and Learning Research Initiative (TLRI) and Ako Aotearoa National Project Fund 2012. A series of “How to” guides and the research report can be downloaded at www.tlri.org.nz/undergraduatemathematics or akoaotearoa.ac.nz/undergraduate-mathematics. The guides are also available for purchase at www.shop.akoaotearoa.ac.nz.
Publisher
Ako Aotearoa – The National Centre for Tertiary Teaching Excellence
PO Box 756
Wellington 6140
Published August 2017 ISBN 978-0-947516-46-8 (online)
Design by Two Sparrows, www.twosparrows.co.nz
This work is licensed under the Creative Commons Attribution-NonCommercial- ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.





