Project description
This project built on previous research showing that insufficient numbers of children reach expected levels of achievement in mathematics. Māori, Pasifika, and students from lower decile schools are particularly disadvantaged. Young children should be given equitable opportunities to develop their mathematical thinking, particularly in all strategy domains of the New Zealand Number Framework. These include not only addition and subtraction (the predominant focus in junior classes), but also multiplication, division, and fractions. This project aimed to provide children with learning opportunities and challenges within the context of multiplication and division, with the goal of developing greater understanding of part–whole relationships in mathematics.
Methodology
The research question posed was:
How do learning experiences using multiplication and division contexts help young children develop understanding of part–whole relationships in mathematics?
The project used a design study and was undertaken as a partnership between researchers and practitioners. Together, we developed a mathematics programme focused on enhancing the development of young children’s part–whole thinking, using multiplication and division problem-solving contexts. A variety of data collection methods was used. These included semi-structured interviews with teachers, individual diagnostic task-based interviews with the children, observations including video-recorded accounts of classroom activities during the teaching, children’s individual project books, and modelling books. Researchers and teachers also kept reflective journals.
The participants in the study were from a culturally diverse decile 5 urban school. There were two teachers in the first year of the study (Years 1 and 2) and in the second year, four teachers (with additional funding from the school and university for two of these teachers) from Years 1 to 3. The experience of the teachers ranged from one year to 24 years. The participants in the first year were 15 Year 1 and 19 Year 2 children. In this group there were 12 New Zealand European, eight New Zealand Māori, five Pasifika, four Asian, and five African students. One-third of the group was English language learners. The participants in the second year were 35 Year 1, 24 Year 2, and 25 Year 3 children. This group consisted of 28 New Zealand European, 28 New Zealand Māori, 8 Pasifika, 18 Asian, and two African. One-quarter of this cohort was English language learners. In both years of the study, there were equal numbers of boys and girls.
The quantitative data from the children’s diagnostic interview were entered into a database for analysis using the Statistical Package for the Social Sciences (SPSS). The qualitative data (interviews and classroom teaching videos) were transcribed and entered into NVivo for coding and analysis.
The study
The study began with the researchers and teachers sharing current understandings about the role of multiplication and division contexts in developing part–whole relationships in mathematics. An individual diagnostic task-based interview was developed by the researchers in conjunction with the teachers and teacher researcher. There was a variety of tasks focused on number knowledge, number operations, and interpretation of representations for two-digit numbers.
In each year there were two dedicated four-week teaching blocks, one in May and the other approximately three months later. The researchers and teachers designed the instructional word problems and selected material to support children’s learning. This material included pairs of baby socks, Unifix blocks, egg cartons, card material for groups of two and five (e.g., five candles on a cake, jeeps with five wheels). Each teaching session began with a problem to be shared by the whole class, and solution strategies (including how the children used materials) were recorded by the teacher in a class modelling book (Figure 1). The Year 3 teacher used the interactive whiteboard as an e-modelling book.
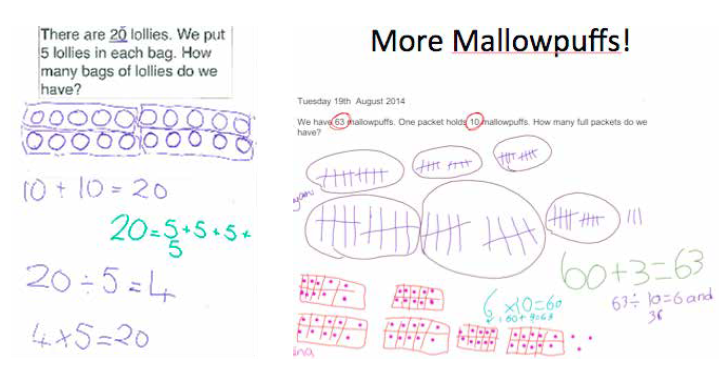
Figure 1. Year 1 modelling book (left) and Year 3 interactive whiteboard as an e-modelling book
The children then worked on a similar problem in their project books and chose appropriate numbers to work with. The empty brackets meant students could also self-select a more challenging number for the day’s problem (Figure 2).
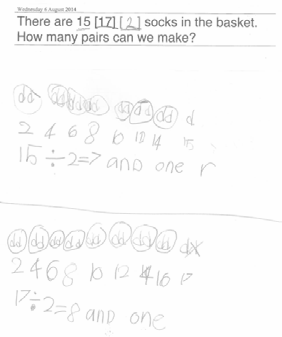
Figure 2. Example of Year 1 child’s project book showing division into groups of two with remainder (odd numbers)
The problems were scaffolded beginning with multiplication and groups of two, then five.
Seven children each have a pair of gumboots. How many gumboots are there altogether?
There are 4 cakes on the table. Each cake has 5 candles. How many candles are there altogether?
These problems were followed by division into groups of two and groups of five. Two types of division problems were used: firstly partitive, where objects are shared evenly among a given number of groups, and secondly quotitive, where groups of a particular size are taken out from a larger quantity.
Mrs L has 10 lollipops. She shares them fairly between 2 children. How many lollipops does each child get? (Partitive division)
There are 15 marbles. We put 5 marbles in each bag. How many bags of marbles are there? (Quotitive division)
We then introduced groups of ten (multiplication) and finally quotitive division into groups of ten (firstly whole decades and then into tens with remainder) which led nicely to supporting place-value understanding (Figure 3).
There are 3 egg cartons. Each carton holds 10 eggs. How many eggs are there altogether? (Multiplication)
There are 20 chocolates. Each tray holds 10 chocolates. How many full trays are there? (Quotitive division, multiples of 10)
There are 34 biscuits. Each packet holds 10 biscuits. How many full packets are there? (Quotitive division with remainder)

Figure 3. Example of a Year 2 child’s work showing quotitive division task into groups of ten with remainder (ones)
The lessons
A common lesson structure was followed in each class with the teachers leading the whole-class discussion, and the researchers working alongside the teachers during the introduction of the problem and follow-up phase where the children worked independently on parallel problems. The lesson usually began with teachers spending five to ten minutes on a number knowledge warm-up activity. For example, Jo would roll a large dice and each child would make a pattern on their paper plates with counters showing the number that was ‘one more than’ the quantity displayed on the dice. We wanted children to learn to make connections between the ‘number just after’, ‘the number one more than’ and ‘the number plus one,’ so their knowledge of sequence became connected to concepts of quantity. In the Year 3 class, Jackie would use a place-value knowledge warm-up activity on the interactive whiteboard (see www.dreambox.com/teachertools). The objective of the number knowledge warm-up activities was to get children focused on the specific mathematical concepts, to be working in the mathematics register (Lager, 2006), and to be using appropriate mathematics equipment such as ten-frames.
In the next phase of the lesson, the day’s multiplication or division problem was introduced in a modelling book (a large scrap book). If new material (e.g., socks, Unifix cubes) was introduced, there was a brief time of exploratory play before using it for instructional purposes. The children and their teacher read the word problem together and particular words were highlighted (e.g., each, pair, altogether, groups of, full) and the teacher discussed these words with the children to ensure that they understood the problem, both the context of the problem and the arithmetic computation. We were very aware of the language needs of the children, particularly the English language learners, and that words take on particular meanings in mathematics.
Children’s names, particular to each class, were often incorporated in the problems along with two characters (Dog and Rabbit) who had been part of the initial diagnostic interview. The children collectively modelled a solution to the problem. Materials were always available and reflected the context of the problem (e.g., pairs of baby socks, egg cartons—two rows of five compartments). The teacher then selected children to model the problem, and asked appropriate questions that encouraged children to focus on the actions used to solve the problem. Other children were asked to revoice or describe the actions. As the children completed different parts of the problem and offered ways of recording their thinking “like a mathematician”, the teacher recorded these ideas as equations in the modelling book. Connections were made between operations; for example, checking the multiplication using repeated addition, and checking the quotitive division using multiplication (inverse operation), or repeated subtraction. The modelling book provided a summary of the class efforts (see Figure 1), and sometimes a child’s name was put next to particular pictures or equations to acknowledge individual contributions.
Each child had an individual project book with the day’s problem pasted in, ready for independent follow-up work. This problem, with the same wording as the class problem, had different numbers, with a choice of two numbers for each problem. In later problems, a space was provided (using [ ]) for children to insert their own number. The children called this option the “mystery number”, and they mostly opted for numbers that provided an appropriate level of challenge (see Figures 2 and 3). If the children needed materials to solve the problem, these were readily available. The children worked independently at group tables on the day’s problem and were encouraged to show their thinking in their project books using pictures and then equations. In each lesson, children were encouraged to complete at least one, if not two problems.
Key findings
Student learning
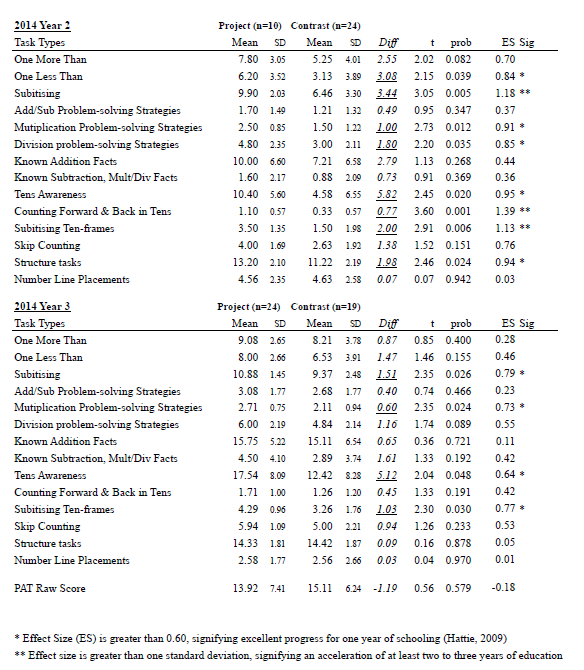
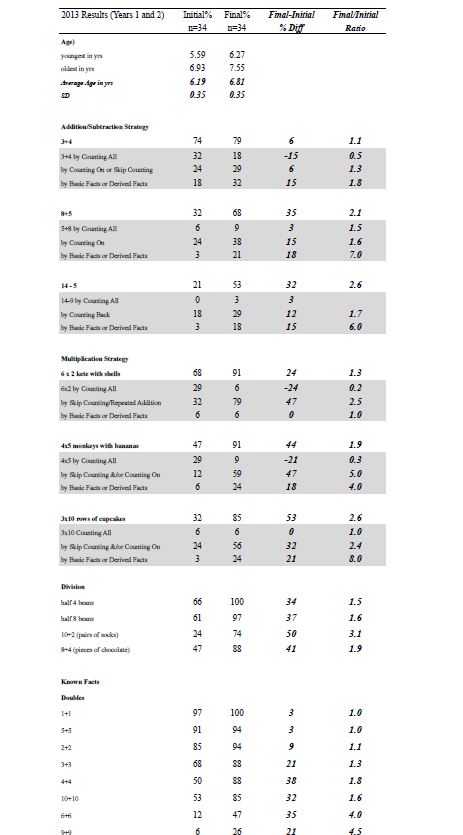
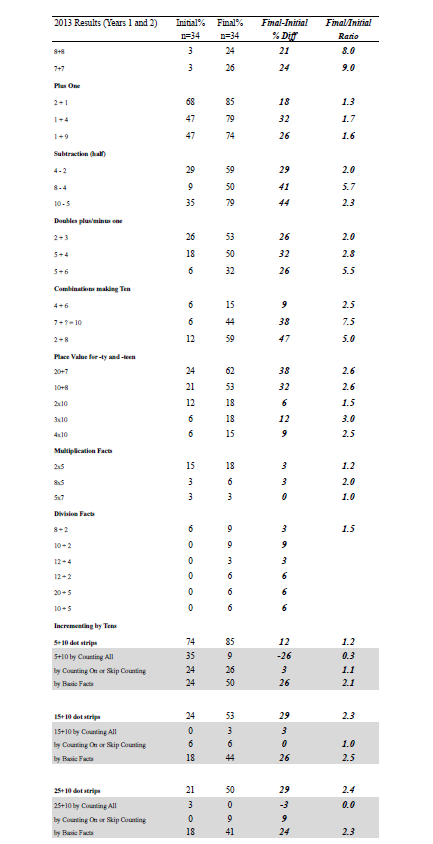
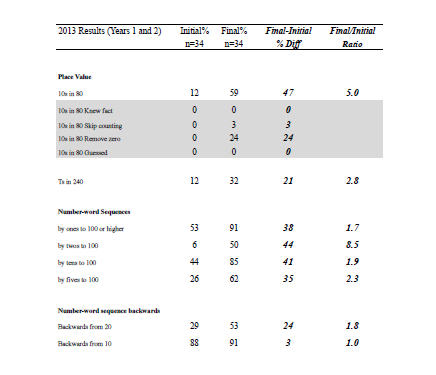
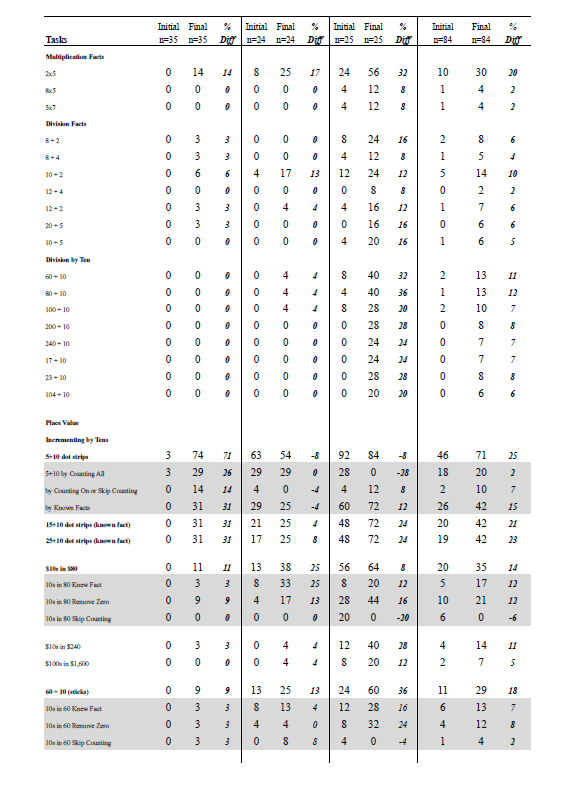
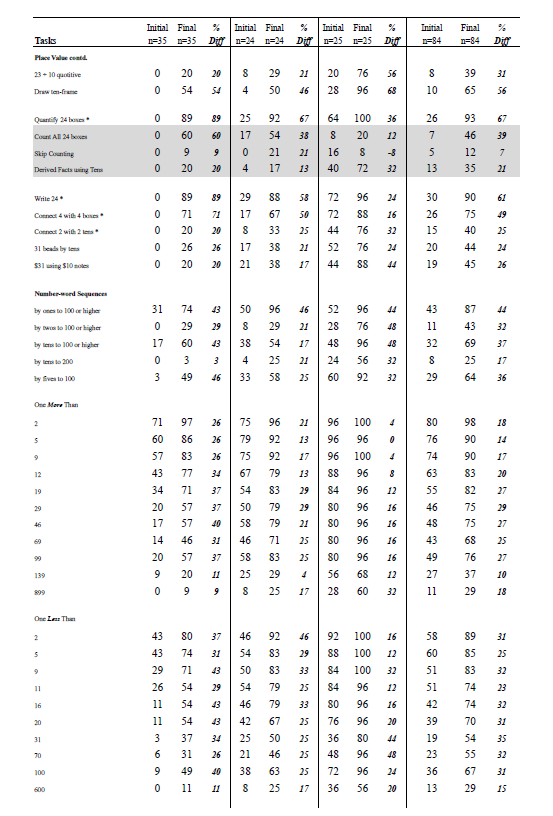
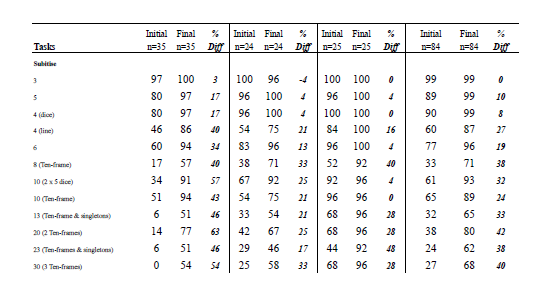
The pre- and post-assessment data were used to generate these findings. The first set of findings is based on assessment data gathered in 2013 from two individual interviews (n=34), one in April and the other in October for Years 1 and 2 (see Appendix A). The second set of findings is from assessment data collected from interviews in April and September in 2014 for Year 1 (n=35), Year 2 (n=24), and Year 3 (n=25) (see Appendix B). Data for each type of task used in 2013 and 2014 were aggregated to create a score at the start and the end of each year of the project, and effect sizes were calculated for the difference between initial and final data (see Appendix C). An effect size is a standardised measure of difference. According to Hattie (2009), an effect size greater than 0.60 signifies excellent progress for one year of schooling. Effect sizes were also calculated separately for Year 2 and 3 at the beginning of 2014 using a comparison of project children with “contrast” children who were new to the class (see Appendix D).
Progress of Year 1 and Year 2 in 2013
Children made progress in addition and subtraction after their work with multiplication and division (see Appendix A). For example, there was improvement of approximately twice as many children who were successful in solving 8 + 5 and 14 – 5 at the end of the project compared to the start. The children moved from using a “counting all” strategy (reflected in a negative value) to more sophisticated strategies such as “counting on” or “derived facts” (part–whole) strategies. The effect size for improvement on addition and subtraction problem solving was 1.14, almost double the 0.60 magnitude that Hattie (2009) claims signifies excellent progress for one year of schooling (see Appendix C). The improvement in proportion of children able to solve four groups of 5 bananas and three rows of 10 cupcakes also was close to double (effect size for improvement in multiplication = 1.46). Again children moved away from “counting all” (a decrease) to “skip counting” or “derived facts” strategies. Children made notable progress on several division tasks, including halving a group of 4 beans, halving 8 beans, putting 10 socks into pairs, and sharing 8 pieces of chocolate among 4 children (effect size for improvement in division = 2.56).
There was also a noticeable improvement in children’s recall of number facts, including the larger single-digit doubles, apart from 5 + 5 which most children already knew. Other known facts that improved were 8 – 4, 10 – 5, 5 + 4, 7 + ? = 10 and 2 + 8. Children’s knowledge of both 20 + 7 and 10 + 8 improved substantially (effect size for improvement in known facts = 1.50). These items are important for place-value understanding and the knowledge of how a multiple of ten is combined with a single-digit quantity. There was a similar improvement in knowledge of the number of $10 notes needed to buy a toy costing $80 (effect size for improvement in tens awareness = 1.52).
Number–word sequences improved, such as counting to 100 by ones, by twos, by fives, and by tens (effect size for improvement in skip counting = 1.32). There was greater awareness of pattern and structure as reflected in the children’s drawings of a 2-by-2 window (effect size for improvement in structure tasks = 1.37).
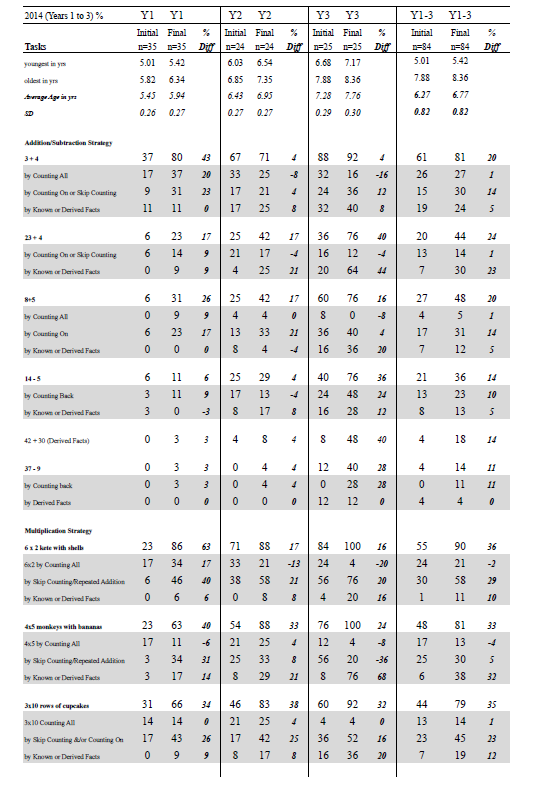
Progress of Year 1, Year 2, and Year 3 in 2014
In this section, we report the progress on selected tasks for each year level separately (see Appendix B). Children made progress in addition and subtraction, but this varied according to the year level of the children. For example, Year 1 children showed a substantial gain on 3 + 4, and Year 3 children made notable improvements on 23 + 4. Much of the improvement in Year 3 children was because of an increase in those who used a “derived fact” (part–whole) strategy to solve this problem. Year 3 children also made notable gains on 14 – 5, and even greater improvement on 42 + 30 (effect size for addition and subtraction was 0.77).
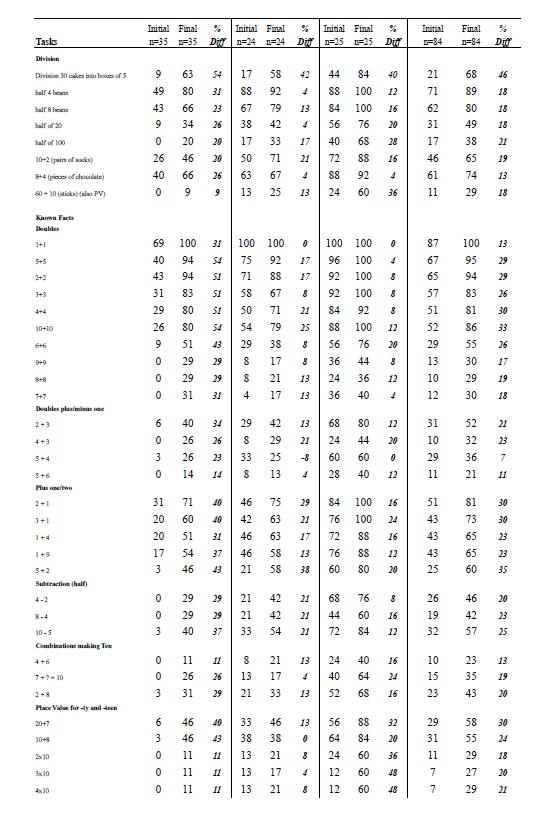
The Year 1 children made the greatest progress on the multiplication tasks. There was a fourfold increase in the numbers who could successfully find the answer to six groups of 2 shells inside mini kete. This could be explained by the improvement in using skip counting by twos or repeated addition to work out the answer. Year 1 and Year 2 students both improved noticeably on four groups of 5, and although the improvement for Year 3 was more modest, there was a substantial improvement in the proportion that used known or derived facts to solve this problem. All three year-groups improved notably on solving three groups of 10 (effect size for multiplication was 1.30). Similarly, there was a substantial increase in the proportions of students who could divide 30 into groups of five and find half of a quantity (effect size for division was 1.05).
Year 1 and Year 2 children made considerable improvement in recall of known facts, particularly single-digit doubles and 10 + 10. Other facts that greatly improved were those involving “plus one” (2 + 1, 3 + 1, 1 + 9), “plus two” (5 + 2), and the combination of tens and ones, such as in 20 + 7 and 10 + 8. Year 3 children made notable improvements in multiplication facts for groups of 5 and 10 (2 x 5, 2 x 10, 3 x 10, 4 x 10) and division into groups of 10 (60 ÷ 10, 80 ÷ 10). This improvement was also evident in the task asking how many “bunches” of 10 sticks could be made from a bag containing 60 sticks. There was substantial improvement in the numbers of Year 3 children who could divide 23 by 10 (division with remainder), and considerable improvement in the number of children connecting the “2” in “24” with two groups of 10 objects, and correctly made $31 quickly with $10 notes and $1 coins (effect size for tens awareness was 1.34).
All three year-groups improved markedly in counting by ones to at least 100. They also improved substantially in their skip counting by twos, fives, and tens. Year 1 children made notable gains in “one more than” and “one less than” relationships.
Subitizing multiples of 10 (two 5-dice, a ten-frame, and ten-frames combined with single dots) was an area of substantial improvement, particularly for Year 1 children. The biggest improvement was in the ten-frame tasks. For Year 3 children, the greatest improvement was on the two ten-frames combined with three single dots (effect size for subitizing was 1.17).
In 2014, for all task types (apart from number-line placement), the effect sizes were above 0.60. Six of the task types, including subitizing, multiplication problem-solving strategies, division problem-solving strategies, recall of known addition facts, tens awareness (place value), and skip counting, were greater than one standard deviation, signifying an acceleration of at least two to three years of education (Hattie, 2009).
Effect of 2013 intervention at beginning of 2014 for Year 2 and Year 3 (project vs. contrast)
At the beginning of the second year of the project, students in the four classes were assessed for the purposes of base-line assessment, and students from the previous year’s project who had moved into other classes were also assessed (see Appendix D). This made it possible to assess the effect of the project in the previous year, as all Year 2 and Year 3 students who were new to the project could be used as contrasts (equivalent to control groups) for the students who had participated in the project in either Year 1 or Year 2 the previous year. We used t-tests (a statistical test for the size of the difference) for each cluster of tasks at the Year 2 and Year 3 levels, and corresponding effect sizes calculated. Project children performed significantly better on the tasks for “one less than” relations, subitizing, multiplication problem solving, division problem solving, tens awareness, counting forwards and backwards in tens, subitizing ten-frames, and pattern and structure tasks. Effect sizes for these tasks ranged from 0.84 to 1.39 standard deviations, showing that the effect of the project was substantial (Hattie, 2009).
At the Year 3 level, there were significant differences for project children on subitizing, multiplication problem solving, tens awareness, and subitizing ten-frames. Progressive Achievement Test data showed that on a written test of mathematics, the Year 3 project children achieved slightly lower (though not significantly) than the contrast children. This shows that the contrast children were not a less capable group in terms of mathematics generally, and that using them as contrasts was legitimate. However, it is likely that some children had not had the advantage of working with multiplication and quotitive division before the baseline assessment tasks were given. Effect sizes for these task types ranged from 0.64 to 0.79, magnitudes that are in the moderate to large range (Fan, 2001).
We acknowledge that during the period of time between the two assessments the children were continuing to learn in mathematics lessons so we are not claiming that all progress can be attributed to this project. However, the substantial improvements are noteworthy and the teachers and researchers believe that some credit can be given to the effect of this project.
Teacher change
We examined the teacher interview data and video footage using key themes to explore both espoused and observed changes in teacher knowledge and pedagogical practices at the start and end of the project. The teachers developed high-leverage practices (Ball, Sleep, Boerst, & Bass, 2009) that included designing authentic word problems, leading effective whole-class discussions, modelling, recording using a modelling book, and developing independent and challenging follow-up problems. The teachers acknowledged their growth in understanding about young children’s ability to work with “groups of”, especially when the contexts were familiar and problems accessible. This focus on accessibility in terms of context and language was a regular challenge for the whole research team. We used meaningful contexts (related to children’s interests, familiar material, and current class topics) and provided opportunities for young children to work with large numbers. All teachers (and researchers) appreciated the difficulty in writing concise problems using suitable language that also matched the intended problem type (e.g., quotitive division).
Multiplication and division problems
Teachers reported a greater understanding about both multiplication and division. There was a shift from talking about multiplication as “times” to “groups of” as they recognised how this better matched the children’s modelling of problems. During initial teaching of division there was confusion between partitive and quotitive division problems. However, by the end of the study, teachers confidently worked with both types of division problems and could articulate the difference between equal share (partitive) and grouping (quotitive) division word problem. At times they felt that some children still confused the notions of “how many groups” and “how many in each group”. There were also challenges when the children first learned about division; as one teacher noted, “they tended to apply the same pattern and strategy of solving multiplication problems to division problems”. However, as children came to understand the concept of “groups of”, both teachers and children used multiplication more readily to check division. As one teacher explained, “some children are beginning to use multiplication to prove their thinking with division … so when we say ‘give us some evidence’ or ‘prove it’ they understand the concept of ‘groups of’ and they are beginning to turn it around”.
The Year 1 teachers found it encouraging to see young children partitioning numbers and engaging in part– whole thinking when it is commonly not expected of them at this level. Another teacher explained that she felt her children were doing more “breaking up of numbers and putting them back together”. By the end of the study, the Year 3 teacher felt that no children in her class were still counting in ones and that they were using skip counting in a meaningful way.
Multiple representations
One change in pedagogical practice was to make more use of multiple representations in the mathematics lessons. These included manipulatives, symbols, diagrams, and online resources. In every lesson the teachers used manipulatives to support student learning in multiplication and division. These included number fans, socks, picture cards (showing contextualised groups of twos, fives, and tens), ten-frames, hundreds boards, egg cartons, and Unifix cubes. Most of the teachers showed greater confidence in supporting student learning (using the modelling book) by encouraging multiple representations and accurate recording of student learning using equations. Usually the teachers recorded in the modelling book and occasionally children were called upon to record their thinking in the book. Student names were often recorded to show whose strategy was recorded and this provided formative assessment data and also a record that students could refer back to for supporting subsequent problem solving. Teachers encouraged children to “write equations like a mathematician” and use the “x” and “÷” symbols, and inverse operations for checking solutions. The ten-frame became a key model and representation when working with groups of ten. Two teachers explicitly taught children to draw a ten-frame and some children initially created a ten-frame by drawing five horizontal lines in the rectangle, thus making 12 squares. In the Year 3 class, the children made the connection with tally marks, where the four initial tally marks divides the rectangle into five units and the fifth line from the tally (the horizontal) divides the rectangle into ten equal units. All teachers encouraged children to choose from a variety of equipment (including that structured in groups of 10) to model solutions. Additionally, they were required to record their thinking in individual project books using multiple representations, including drawings and equations. This use of multiple representations enabled students to connect their knowledge and skills to the new mathematical situations.
Learning environment
One teacher reported grappling with grouping and the legacy of the Numeracy Development Project to group learners according to strategy stage. The teacher explained: “I couldn’t get my head around having three or four groups, all working on a different strategy with different numbers”. As part of the project, the teachers set up a routine where the class worked together on one problem each day, encouraged independent thinking, and modelled recording in conjunction with the teacher–student and student–student interactions. The teachers listened carefully to the children’s ideas, made decisions about whom to select to share thinking, and led the children to think about multiplication as “groups of” and division (quotitive) as making equalsized groups of a particular size. Instead of grouping the children by ability, they all worked on a problem differentiated in terms of the magnitude of the numbers. Manipulatives were readily available for children to support their thinking and they recorded drawings and equations in their project books.
Implications and limitations
It is evident from this study that students benefitted from working with multiplication and division problemsolving contexts. The findings show that young children recognise and can work with groups of items and count in twos, fives, and tens. This means that junior class teachers need to look beyond activities and experiences emphasising counting in singletons (ones), and to also provide experiences with different groups of quantities. This is supported by current research in Australia by Mulligan and Mitchelmore (2013) focusing on the importance of pattern and structure and a move away from arithmetic thinking alone towards appreciating the spatial dimension of number, and making connections across strands. The power of the quotitive division problem cannot be underestimated. Constructing groups of ten enabled naturally occurring links to place value through meaningful problems, instead of non-contextualised “bundling of tens” activities.
It takes time, resources, and commitment to sustain a study focused on improving student outcomes through a change in teacher practice. In this study we were fortunate to have all of these. Considerable time was spent designing instructional problems and preparing resource material. It was through our regular professional discussions that we came to appreciate the complexity of the work but also how much we were questioning current practices and the challenges presented by our objective. One teacher, in her reflection, offered the following as ideas when considering the question: Where to next? She would like to repeat and refine the project experience, incorporate more explicit teaching (e.g., recording on a ten-frame), make greater use of differentiated problems, use flexible small-group teaching to support targeted children on specific concept and skill development, explore children writing their own problems, and incorporate the reflection circle (borrowing the strategy from written language) where children share their “aha” moments or what helped them solve the problem when they had found it challenging.
One outcome of the study was an appreciation of the powerful links to place-value understanding. Together, we want to explore these ideas further and build on current thinking in relation to pattern and structure. From this study, we need to consider not only sustaining this work but building on these ideas and capitalising on the power of generative change.
Conclusion
This study challenges prevailing and persistent views that young children in their first years of schooling focus on number sequences and number knowledge up to 20, counting by ones, and the operations of addition and subtraction. Providing children with the experience of constructing groups of ten was valuable for helping strengthen place-value understanding and is consistent with literature claiming that place value is inherently multiplicative (Bakker, van den Heuvel-Panhuizen, & Robitzsch, 2014). Many effect sizes for aggregated task types were greater than one standard deviation, which according to Hattie (2009) corresponds to an acceleration of between two and three years of schooling (based on an average effect of d = 0.20 to d = 0.40 per year for student achievement). The findings show how by providing young children with learning opportunities and challenges within the context of multiplication and division, they develop greater understanding of part–whole relationships in mathematics. This study demonstrates the power of practicebased teacher education in raising mathematics achievement, particularly for priority learners.
References
Bakker, M., van den Heuvel-Panhuizen, M., & Robitzsch, A. (2014). First-graders’ knowledge of multiplicative reasoning before formal instruction in this domain. Contemporary Educational Psychology, 39(1), 59–73.
Ball, D. L., Sleep, L., Boerst, T. A., & Bass, H. (2009). Combining the development of practice and the practice of development in teacher education. The Elementary School Journal, 109(5), 458–474.
Fan, X. (2001). Statistical significance and effect size of educational research: Two sides of a coin. The Journal of Educational Research, 94, 275–282.
Hattie, J. A. C. (2009). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. London, England: Routledge. Lager, C. A. (2006). Types of mathematics-language reading interactions that unnecessarily hinder algebra learning and assessment. Reading Psychology, 27(2-3), 165-204.
Mulligan, J. T., & Mitchelmore, M. C. (2013). Early awareness of mathematical pattern and structure. In L. D. English & J. T. Mulligan (Eds.), Reconceptualizing early mathematics learning (pp. 29–46). New York, NY: Springer.
Outputs
2015 Publications
Young-Loveridge, J., & Bicknell, B. (2015). Using task-based interviews to assess early understanding of number. In C. Suurtamm (Ed.), Annual Perspectives in Mathematics Education (APME) 2015: Assessment to enhance learning and teaching (pp. 67–74). Reston, VA:NCTM.
Young-Loveridge, J., & Bicknell, B. (2015). Using multiplication and division contexts to build place-value understanding. In X. Sun, B. Kaur, & J. Novotná (Eds.), Proceedings of the TwentyThird International Congress of Mathematics Instruction (ICMI23): Primary mathematics study on whole numbers (pp. 379–386). Invitational conference, Macau, China. 3–7 June, 2015.
Bicknell, B., & Young-Loveridge, J. (2015). Young children’s number-line placements and place-value understanding. In M. Marshman, V. Geiger, & A. Bennison (Eds.), Mathematics in the margins (Proceedings of annual conference of Mathematics Education Research Group of Australasia) (pp. 101-108) Sunshine Coast: MERGA.
Young-Loveridge, J., & Bicknell, B. (2015). Using multiplication and quotitive division contexts to provide foundational place-value understanding. In K. Beswick, T. Muir, J. Wells (Eds.), Proceedings of 39th conference of the International Group for the Psychology of Mathematics Education), (Vol. 1, p. 212). Hobart, Australia: PME.
Bicknell, B., & Young-Loveridge, J. (in press). Using problems solving and representations to build number knowledge. Proceedings of International Symposium for Elementary Mathematics Teaching (SEMT), Charles University, Prague, Czech Republic, 16–21 August 2015.
Bicknell, B., & Young-Loveridge, J. (under review). Teacher-researcher partnership: Working together to enhance young children’s learning in mathematics. In R. McNae & B. Cowie (Eds.), Realizing innovative partnerships in educational research. Rotterdam, The Netherlands: Sense.
Bicknell, B., Young-Loveridge, J., Lelieveld, J., & Brooker, J. (under review). Using multiplication and division contexts with young children to develop part–whole thinking. Set: Research Information for Teachers.
2014 Publications
Young-Loveridge, J., & Bicknell, B. (2014). Developing young children’s understanding of place-value using multiplication and quotitive division. In C. Nicol, S. Oesterle, P. Liljedahl, & D. Allan (Eds.), Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics Education (PME) and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education (PME-NA) (Vol. 5, pp. 409–416). Vancouver, Canada: PME.
Young-Loveridge, J. & Bicknell, B. (2014). Supporting the development of number fact knowledge in five- and six-year-olds. In J. Anderson, M. Cavanagh, & A. Prescott (Eds.), Curriculum in focus: Research guided practice. Proceedings of the 37th annual conference of the Mathematics Group of Australasia (pp. 669–676). Sydney, NSW, Australia: MERGA.
2013 Publications
Young-Loveridge, J., & Bicknell, B. (2013). Introducing multiplication and division contexts in junior primary classes. Teachers and Curriculum, 13, 70–76.
Young-Loveridge, J., & Bicknell, B. (2013). Using multiplication and division tasks to support young children’s part–whole thinking in mathematics. In J. Novotná & H. Moraová (Eds.), Tasks and tools in elementary mathematics: [Keynote address] in Proceedings of the International Symposium for Elementary Mathematics Teaching: SEMT13 (pp. 55–66). Prague, Czech Republic: Charles University.
Young-Loveridge, J., & Bicknell, B. (2013). Using multiplication and division contexts with young children: Crossing the boundary from counting to part–whole processes. In T. Dooley, S. NicMhuirí, M. OReilly, & R. Ward (Eds.). Mathematics education: Crossing boundaries: [Keynote address] in Proceedings of the Fifth Conference on Research in Mathematics Education: MEI 5, (pp. 33–51). St Patrick’s College, Drumcondra, Dublin City University, Dublin, Ireland.
2015 Conference presentations and workshops
Bicknell, B., Young-Loveridge, J., & Simpson, J. (2015, March). Using division problem-solving contexts to build place-value understanding.
Workshop presented at the Primary Mathematics Association one-day seminar, Waipuna Conference Centre, Auckland.
Young-Loveridge, J., & Bicknell, B. (2015, June). Using multiplication and division contexts to build place-value understanding. Paper for the TwentyThird International Congress of Mathematics Instruction (ICMI23): Primary Mathematics Study on Whole Numbers. Invitational conference, Macau, China. 3–7 June, 2015.
Bicknell, B., & Young-Loveridge, J. (2015, June). Young children’s number line placements and place-value understanding. The 38th annual conference of the Mathematics Education Research Group of Australasia, Sunshine Coast, 28 June–2 July 2015.
Young-Loveridge, J., & Bicknell, B. (2015, July). Using multiplication and quotitive division contexts to provide foundational place-value understanding. Paper for the annual conference of the International Group for the Psychology of Mathematics Education (PME), Hobart, Tasmania, 13–18 July, 2015.
Bicknell, B., & Young-Loveridge, J. (2015, August). Young children’s number line placements and place-value understanding. Paper for International Symposium for Elementary Mathematics Teaching, Charles University, Prague, Czech Republic, 17–21 August, 2015.
2014 Conference presentations and workshops
Young-Loveridge, J., & Bicknell, B. (2014, July). Supporting the development of number fact knowledge in five- and six-year-olds. Paper presented at the 37th Annual Conference of the Mathematics Education Research Group of Australasia, Melbourne, Vic, Australia.
Young-Loveridge, J., & Bicknell, B. (2014, July). Developing young children’s understanding of place-value using multiplication and quotitive division. Paper presented at the 38th Conference of the International Group for the Psychology of Mathematics Education (PME) and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education, Vancouver, Canada.
Young-Loveridge, J., & Bicknell, B. (2014, July). Developing number fact knowledge for differing contexts. Paper presented at the Science, Technology, Engineering, Mathematics (STEM) in Education conference, University of British Columbia, Vancouver, Canada.
Young-Loveridge, J., Bicknell, B., & Lelieveld, J. (2014, May). Strengthening place value: Using multiplication and division contexts with young children. Paper presented at the Primary Mathematics Association One Day Seminar, Waipuna Conference Centre, Auckland.
Young-Loveridge, J., Bicknell, B., & Lelieveld, J. (2014, May). Strengthening place value: Using multiplication and division contexts with young children. Paper presented at the Waikato Mathematics Symposium, Melville Intermediate School.
Young-Loveridge, J., & Bicknell, B. (2014, May). Using multiplication and division contexts to enhance part–whole thinking in mathematics. Paper presented at the Technology, Environmental, Mathematics & Science (TEMS) Education Research Centre Autumn Seminar Series, University of Waikato. Hamilton, New Zealand.
2013 Conference presentations and workshops
Young-Loveridge, J. (2013, September). Using multiplication and division contexts with young children: Crossing the boundary from counting to part–whole processes. Invited keynote address to the National Conference of Mathematics Education Ireland (MEI5). St Patricks College, Drumcondra, Dublin City University, Dublin, Ireland.
Young-Loveridge, J. (2013, August). Using multiplication and division tasks to support young children’s part–whole thinking in mathematics. Invited keynote address to the International Symposium for Elementary Mathematics Teaching (SEMT), Charles University, Prague, Czech Republic.
Young-Loveridge, J., & Bicknell, B. (2013, September). Using multiplication and division contexts with young children to enhance their appreciation of number properties. Invited Address at King’s College London, London, England.
Television interview 2013
Young-Loveridge, B., & Bicknell, B. (2013). Television interview with Hillary Entwistle about research on multiplication and division with young children. Aired on TV Central (Channel 30), 9 May at 7.55pm and 10.55pm.
Project Team
Researchers
Dr Brenda Bicknell is an associate professor at the University of Waikato. Her research interest is in young children’s development in mathematics learning and mathematically gifted children.
Dr Jenny Young-Loveridge is an associate professor at the University of Waikato. Her research interests are focused on the development of children’s mathematical thinking.
Participant partner teachers Knighton Normal School, Hamilton:
Jo Lelieveld, John Brooker, Lauren Hodge, and Jackie Simpson
Emerging researcher Angela Vandy, Pirongia School

Back Row: Jenny Young-Loveridge, John Booker, Angela Vandy
Front Row: Brenda Bicknell, Lauren Hodge, Jo Lelieveld, Jackie Simpson
Appendix A
Appendix B
Appendix C
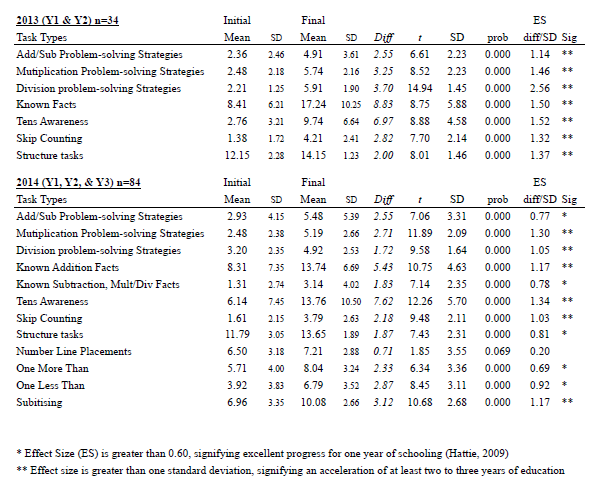
Appendix D