Introduction
The LEMMA project—Learning Environments with Mathematics Modelling Activities—grew out of a concern that many of our mathematics students struggle to use mathematical concepts flexibly to solve problems in the real world. The LEMMA project designed learning environments that encourage students to develop sophisticated conceptual understandings and communication competencies through mathematical modelling activities. Like a lemma in mathematics, LEMMA is not a grand theorem or solution, but merely “a stepping stone to a larger result” (Wikipedia, 2009)—the desired result being improved mathematical competencies among New Zealand secondary school students.
Key findings
- Rich mathematical modelling activities such as model eliciting activities (MEAs) (Lesh, Hoover, Hole, Kelly, & Post, 2000) can elicit a diverse range of mathematical approaches from students that can be a springboard for further mathematical conceptual development.
- Students’ written mathematical communication and mathematical modelling competencies are often at primitive stages of development.
- MEAs need to be supplemented with effective follow-up activities to strengthen students’ conceptual understandings, written mathematical communication, and mathematical modelling competencies.
Major implications
- We have created four sequences of modelling activities that focus on:
-
- circle geometry
- equivalent proportions
- mixing ratios; and
- scale and perspective with volume.
Each sequence includes an MEA and about eight to 10 follow-up activities and assessment activities.
- We have created blueprints for creating follow-up activities to MEAs in the form of design principles and strategies. Teachers and researchers can use these blueprints to create sequences of modelling activities for other mathematical topics.
- We have developed professional development tools that can prepare teachers to create learning environments based on these activities which promote conceptual understanding, mathematical modelling and communication.
The research
The New Zealand government’s goal of creating an internationally competitive knowledge economy largely depends on graduates being able to use powerful conceptual tools to solve real-world problems. One of the most powerful conceptual tools is mathematics, which is heavily used in areas as diverse as finance, engineering, information and communications technology, business, and scientific research. However, there is strong evidence from national and international research (e.g., Stewart & Thomas, 2007; Thompson, 1994; Eisenberg & Dreyfus, 1991) that many mathematics students have impoverished conceptual understandings of key mathematical ideas. Research suggests that although students are reasonably proficient in performing various mathematical techniques and procedures, their ability to apply these procedures successfully to solve real-world problems is severely undermined by their limited conceptual understanding.
If New Zealand is to develop an internationally competitive knowledge economy, we need graduates who possess a wider range of competencies and understandings than our existing learning environments seem to cultivate; we need graduates with mathematical modelling and communication competencies who can leverage their deep conceptual understandings to solve real problems. This need is echoed in the New Zealand curriculum’s recent emphasis on key competencies, all of which are involved in mathematical modelling and communicating. The LEMMA project seeks to address this need by designing and investigating learning environments that cultivate deep conceptual understandings of mathematics alongside effective mathematical modelling and communication competencies.
We addressed three research questions:
- What are useful design principles for creating sequences of activities that encourage students to develop and consolidate deep conceptual understandings and mathematical modelling and communication competencies? Note that design principles already exist for MEAs (Lesh et al., 2000); this project looked at creating design principles for follow-up activities to MEAs.
- What is the nature of the understandings and competencies cultivated in these learning environments? How do these understandings and competencies develop?
- What kinds of tools can teachers use to identify and document the mathematical competencies and understandings that students express and develop during mathematical modelling activities?
Methodology and analysis
We used design experiment methodology (Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003) to develop the sequences of activities, design principles, and teacher tools. The design experiment methodology was chosen because it combines theory and practice to design effective learning environments, which is ideally suited to our project goals:
Design experiments have both a pragmatic bent (“engineering” particular forms of learning) and a theoretical orientation (developing domain-specific theories by systematically studying those forms of learning and the means of supporting them). (p. 9, Cobb et al., 2003)
In this project, we sought to “engineer” a wide range of mathematical understandings and competencies through carefully designed sequences activities, and we sought to study the “means of supporting” these understandings and competencies by creating principles for designing such activities, and teacher tools for implementing these activities.
The design experiments involved a series of iterative cycles of design meetings, field testing, and analysis. Four designers met every 3 to 4 weeks over a period of 2 years. They designed four sequences of activities that focused on equivalent proportions, circle geometry, mixing ratios, and scale and perspective in volume. These activities were tested with pre-service teachers in semi-clinical settings, before being revised and implemented in a range of secondary school classes. Data were collected in the form of videotapes and audiotapes of focus groups, students’ written work, and observer’s field notes. These data were used to inform revisions to the activities. The design team also created teacher tools for implementing these activities that were tested out with inservice teachers in a variety of professional development settings.
Students’ written work was analysed using coding schemes to identify the quality of the students’ written mathematical communication, mathematical modelling competencies, and mathematical approaches. Videotape analysis was conducted on select focus groups to document the development in students’ conceptual understanding, as evidenced by their modelling cycles.
Key finding 1: MEAs can elicit a diverse range of mathematical approaches from students which can be a springboard for further mathematical conceptual development.
Implementations of MEAs with classes of students regularly yielded a diverse range of mathematical approaches. For example, one MEA we designed asks students to create a method for ranking freehand circle drawing attempts from most circular to least circular. In a class of Year 11 students, 10 different mathematical models were developed, which drew on a wide range of mathematical concepts. Three of these are summarised in Figure 1.
| Model A: Construct a line segment connecting any two points A and B on the perimeter of the circle attempt. Construct two perpendicular line segments from points A and B to the where they intersect the perimeter (C and D). Construct a line segment between points C and D. Construct a perpendicular line from point C. Measure the angle ~ between line CD and the perpendicular line. Repeat this process 2 or 3 times, and find the average angle. The circle attempt with the smallest average angle wins. |  |
| Model B: Construct an exscribed square around the circle attempt and use the intersection of the square’s diagonals as the centre. From this centre, find the longest “radius” of the circle attempt rlong, and construct a perfect circle of radius rlong from the centre previously found. Measure the area of the perfect circle that is not covered by the circle attempt—this is called the margin of error. The circle attempt with the smallest margin of error wins. | 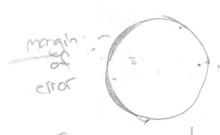 |
| Model C: Fold the circle attempt in half and half again, and use the intersection of the folds as the centre. Measure the length of the folds from the centre to the perimeter. Divide the first length by the second length to obtain a score. The circle attempt with a score closest to 1 wins. | 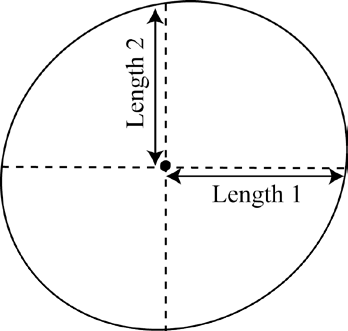 |
Figure 1: Examples of students’ approaches to the circle drawing MEA.
Key finding 2: Students’ mathematical modelling and written mathematical communication competencies are often at primitive stages of development.
Many secondary school students have little experience with authentic mathematical modelling activities. Consequently, students who worked on MEAs often neglected to consider their modelling assumptions, or to test their models on different scenarios. For example, a number of students created mathematical models in response to the circle drawing competition MEA described above that would have allowed a square to win the competition. To consider a specific case, group C’s mathematical model described in Figure 1 involved calculating the ratio of the two lengths formed from a central point in the circle attempt, obtained by paper folding. However, if this method were tested out on a square, the two lengths identified are identical and would yield a perfect score of 1, as shown in Figure 2.
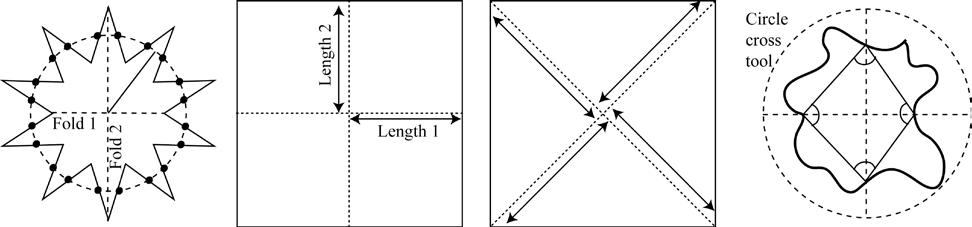 |
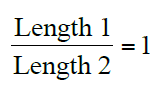 |
Figure 2: According to group C’s method, a square could win a circle drawing competition.
Furthermore, even if students created high quality mathematical models, they often struggled to communicate them effectively in written form. Again, this is likely a consequence of the low emphasis on written mathematical communication in many mathematics classrooms. MEAs expect students to communicate not only the solution, but also the method for finding the solution and the generalisation of the method, and to couch all of this information using clear language that is intelligible to a non-mathematician. However, students struggled to meet all of these requirements. For example, Figure 3 shows a Year 10 group’s solution to a painting MEA in which the client, Nikki, wants 4 litres of “Sail away blue” paint, which she knows is made up of 2 blue:5 white. The students are asked to create a general method for finding the amount of paint needed to create any amount of any shade. Although the students’ general method was correct, it was poorly communicated as it was conflated with the demonstration of the method in two different specific cases.
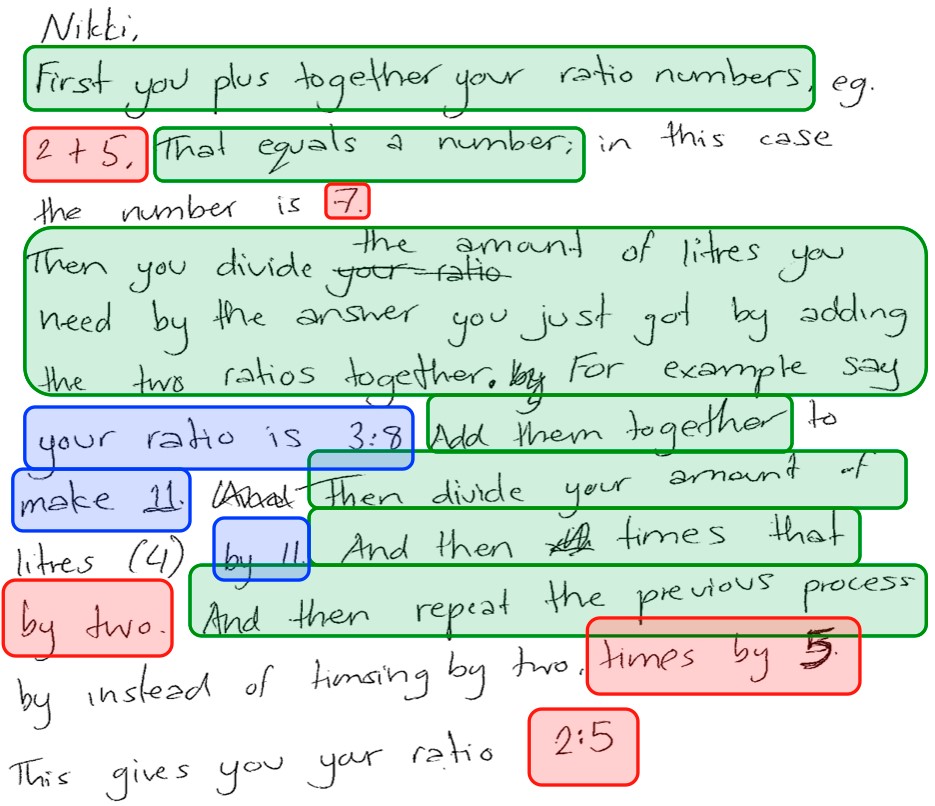
Figure 3: Ron, Helen and Tyler’s letter. Green relates to the general method. Red shows the application of the method to a specific example of a ratio 2:5. Blue shows the application of the method to another ratio, 3:8.
Key finding 3: MEAs need to be supplemented with effective follow-up activities to strengthen students’ conceptual understandings, written mathematical communication, and mathematical modelling competencies.
We developed follow-up activities that were intended to strengthen students’ understandings and competencies that are elicited by MEAs. We used four guiding principles to design these follow up activities:
- Whereas MEAs encourage students to draw on whatever knowledge they have, follow-up activities need to focus students’ attention on specific aspects of mathematics, modelling or communication that are identified as needing further development.
- Follow-up activities need to challenge students to develop the understandings and competencies they demonstrate in MEAs further.
- Follow-up activities need to give students opportunities to consolidate their new understandings and competencies.
- Follow-up activities need to flow on from the MEAs through context and content, thereby capitalising on the initial investment into establishing the context in the MEA, and connecting to the students’ experiences in the MEA.
A productive strategy for fulfilling these principles was to ask students to analyse and extend some aspect of another students’ solution. For example, a follow-up activity to the painting MEA described above asks students to highlight and underline passages from the Ron, Helen and Tyler’s solution in Figure 3 that communicated the general method and its demonstration in specific examples. Students are then challenged to rewrite Ron, Helen and Tyler’s method so that the general method is clearly distinguishable from its demonstration in specific cases.
Major implications for practice
Our research suggests that learning environments that are based on sequences of modelling activities can support the development of students’ conceptual understandings of mathematics as well as their mathematical modelling and communication competencies. We have created four sequences of activities that are suitable for junior secondary school mathematics classes. These focus on the following topics: circle geometry, equivalent proportions, mixing ratios, and scale and perspective with volume. Each sequence begins with an MEA, which is supplemented by about eight to 10 follow-up activities and assessment activities. The follow-up activities focus on various aspects of conceptual understanding, mathematical modelling and communication. Teachers are encouraged to choose follow-up activities that are deemed necessary for the students, based on their performance on the initial MEA.
In addition to these four sequences of activities, we have created blueprints for designing follow up activities to MEAs. These blueprints take the form of design principles and strategies, which can be used by teachers and researchers to design follow-up activities to MEAs that focus on other mathematics topics and year levels. We plan to continue to use these blueprints to design further sequences of activities, and invite interested teachers and researchers to join us.
Finally, we have developed some professional development tools to help teachers create learning environments that are based on these sequences of modelling activities. These involve analysis and observation tools, as well as guidelines for implementing MEAs and follow-up activities. Our research has highlighted that students have limited opportunities to engage and strengthen their mathematical modelling and communication competencies. In a parallel vein, many teachers also have limited experience with implementing authentic mathematical modelling activities in classrooms. Therefore, learning environments that support the development of students’ conceptual understandings, mathematical modelling and communication competencies need to be established alongside professional development for teachers.
References
Cobb, P., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13.
Eisenberg, T., & Dreyfus, T. (1991). On the reluctance to visualize in mathematics. In W. Zimmermann & S. Cunningham (Eds.), Visualization in teaching and learning mathematics (pp. 25–38). MAA Notes #19.
Lesh, R., & Doerr, H. M. (2003). Beyond constructivism: Models and modelling perspectives on mathematics problem solving learning, and teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Lesh, R., Hoover, M., Hole, B., Kelly, A., & Post, T. (2000). Principles for developing thought-revealing activities for students and teachers. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 591–646). Mahwah, NJ: Lawrence Erlbaum Associates.
Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis: An expanded sourcebook, 2nd ed. Thousand Oaks, CA: Sage.
Stewart, S., Thomas, M. O. J. (2007). Embodied, symbolic, and formal thinking in linear algebra. International Journal of Mathematical Education in Science and Technology, 38(7), 927–937.
Thompson, P. W. (1994). Images of rate and operational understanding of the fundamental theorem of calculus. Educational Studies In Mathematics, 26(2,3), 229–274.



