Introduction
Seen by policy makers as both the cause of and a solution for education problems, teacher education is frequently criticised for not producing teachers of sufficient quality, while simultaneously being viewed as “an ideal site for increasing teacher quality, providing it is subject to reform” (Ell & Grudnoff, 2012, p. 79). Calls for reform (Education Workforce Report, 2010; NZTC, 2010) relate to newly qualified teachers’ capacity to respond to the needs of an increasingly diverse student body, alongside changing educational outcomes in terms of knowledge and competencies (Andretti & Major, 2010). Such calls are particularly pertinent to mathematics education. In New Zealand, too many students are disaffected with their mathematics learning experiences, and systemic concerns about mathematics underachievement persist (see Chamberlin & Caygill, 2012).
This project aimed to investigate how changes in our initial mathematics teacher education curriculum and pedagogies could better support prospective teachers to develop a vision of practice, knowledge of students and content, dispositions for using this knowledge, and a repertoire of practices and tools (Hammerness, Darling-Hammond, & Bransford, 2005) that align with current reforms in mathematics education. The ultimate goal for reforms in mathematics education is characterised as “mathematics proficiency” (Kilpatrick, Swafford, & Findell, 2001): a way of knowing in which conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition are intertwined in mathematical practice and learning at every level for every student. This intellectually and socially ambitious goal begs a new conception of teachers’ work—involving teaching diverse learners not only to do mathematics competently, but also to make sense of it and be able to use it to solve authentic problems. Proponents of mathematics education reforms have variously described such teaching as “dialogic”, “reform-oriented”, “responsive” (Stylianides & Stylianides, 2014), “inquiry-based” (Alton-Lee, Hunter, Sinnema, & Pulegatoa-Diggins, 2011), and “responsible” (Ball & Forzani, 2011).
The current conception of what it takes to do the work of ambitious mathematics teaching is informed by a growing body of research aimed at both understanding what teachers need to do to successfully accomplish ambitious mathematical goals (see Anthony & Walshaw, 2007; Lampert, Beasley, Ghousseini, Kazemi, & Franke, 2010; National Council of Teachers of Mathematics (NCTM), 2014; National Mathematics Advisory Panel, 2008) and what they need to know to do it (Ball, Thames, & Phelps, 2008). Underpinned by the belief that all students can “develop positive mathematical identities and become powerful mathematical learners” (Anthony & Walshaw, 2009, p. 6), ambitious mathematics teaching involves skilled ways of eliciting and responding to each and every student in the class so that they learn worthwhile mathematics and come to view themselves as competent mathematicians. Thus it requires a teaching practice in which teachers engage deeply with each student’s thinking, adjusting their instruction accordingly to promote learning. This responsive form of teaching—both in a cultural and equitable sense—is necessary if we are to support meaningful participation for our diverse learners and work to disrupt longstanding assumptions about who can and who cannot do mathematics (Averill, 2012).
Findings from the national Numeracy Development Project and previous TLRI classroom studies in mathematics (e.g., Anthony & Walshaw, 2006; Young-Loveridge, 2010; Hunter & Anthony, 2011) suggest that access to exemplars of ambitious teaching is limited within the New Zealand context. Moreover, at the time of conceptualisation of this project there was a notable lack of research concerning practices within teacher education that would enable prospective teachers to learn to enact key practices of ambitious mathematics teaching in principled ways, using knowledge of subject matter and knowledge of students appropriately (Ball & Forzani, 2009).
The current project joins a growing body of educational research (e.g., Ball, Ben-Peretz, & Cohen, 2014; Ghousseini & Herbst, 2014; Lampert et al., 2010; McDonald, Kazemi, Kelley-Petersen, Mikolasy, Thompson, Valencia, & Windschitl, 2014; Santagata, & Yeh, 2014) that explores what has been characterised in the international literature as “the turn to practice-based education” (Zeichner, 2012). The premise of the emergent studies is based on the belief that in order to better support prospective teachers to learn to do ambitious teaching we need to teach them both the interactive skills required to engage students in serious mathematics work, and to be able and willing to use this knowledge in particular moments of practice. Like others, we argue (Anthony & Hunter, 2012) that preparing prospective teachers for doing the complex work of ambitious mathematics teaching requires that we implement different pedagogies of teacher education in deliberate ways that make teaching a central focus.
The research
Looking to change the ways we as mathematics teacher educators support prospective teachers learning the work of ambitious mathematics teaching required that we focus more closely on the relational aspect of teaching—how teachers manage and interpret complex forms of interaction in which students construct their own understanding and learn from one another. We wanted to develop and investigate the enactment of new instructional activities and pedagogies that enable prospective teachers to investigate authentic problems of practice and develop knowledge and skill in the contexts of their use. Previously, our links to the practice of teaching involved prospective teachers in examining “representations” of teaching (e.g., video records or written student work), micro-teaching experiences, and reflective discussions around practicum experiences. However, like others (e.g., McDonald, Kazemi, & Kavanagh, 2013; Ghousseini & Herbst, 2014), we felt that examining representations of practice was not sufficient in terms of preparation for ambitious teaching.
To advance our understanding of how to design instructional activities and enact pedagogies of practice that support prospective teachers to think systematically about the complexities of practice and develop pedagogical skills in the interactive aspects of teaching, we posed the following research questions:
Research focus and questions
- Focus 1: Design of instructional activities that support pedagogical practices associated with ambitious teaching of mathematics
- How can we design activities for instruction for teaching ambitious practices that takes into account the need for prospective teachers to both accumulate new knowledge and skills and be able to use them appropriately in the classroom contexts?
- Focus 2: The enactment of the design
- How can mathematics teacher educators enact that instructional design in ways that support prospective teachers to do ambitious mathematics teaching?
- Focus 3: The learning of practice by prospective teachers
- How do prospective teachers learn the work of ambitious mathematics teaching?
- What do they learn, in terms of practices, knowledge, and skills, and how to use them in ways that are adapted to particular learners in the classroom?
- What are constraints and affordances on prospective teachers’ learning opportunities?
- Focus 4: Learning from teaching
- How does prospective teachers’ learning of core practices transfer to the classroom?
- How does teachers’ professional noticing continue to support newly qualified teachers’ learning?
- What are the constraints and affordances on enactment of ambitious mathematics teaching in the classroom?
- Focus 5: The learning of teacher educators
- In reforming their curriculum towards pedagogies of practice what do mathematics teacher educators learn?
Research design and methods
The study was multilayered and conducted across multiple sites and multiple programmes. The research team was involved in self-study and collaborative interactions with other researchers and teacher educators and prospective teachers. We used design study as our methodology. Design study seeks to both provide “systematic and warranted knowledge about learning, and to produce theories to guide instructional decision-making towards improved student learning” (Confrey, 2006, p. 136). Our aim was to support the “constitution of an empirically grounded local instructional theory that underpins that instructional sequence” (Gravemeijer & Cobb, 2006, p. 45).
Conducted in the complexity of authentic learning settings, our design setting involved the study of new instructional strategies and tools in relation to learning goals associated with learning the work of ambitious mathematics teaching (see figure 1). As such, design study methodology enabled us to address both at a practice-based pedagogical level and a theoretical level the exploration of the instructional dynamic that constitutes teaching and learning (Ball & Forzani, 2009; Thames and Zoest, 2013).
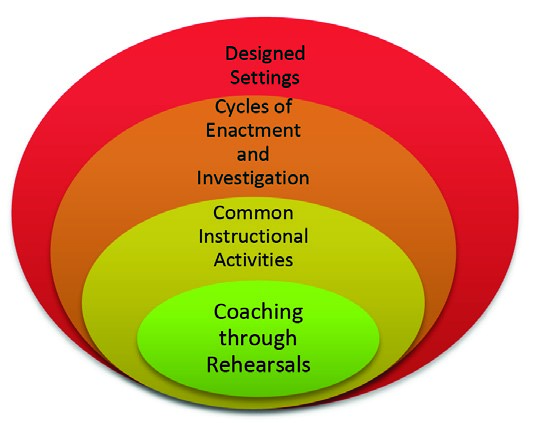
Figure 1: Design study model
To address issues of accountability in initial teacher education (Louden, 2010) we also felt it important that we investigate the effect of our intervention beyond the teacher education setting (see focus 4). To investigate the potential for generative teacher learning—in terms of teacher capability and disposition—we adopted a case study approach involving a small group of graduating teachers. In the third year of the project we worked with a small sample of graduating teachers to look closely at the enactment of core practices promoted within their initial teacher education programme and the development of dispositions associated with adaptive expertise (Lampert, 2010; Timperley, 2013). Data included classroom observations, post-lesson interviews and, for the primary group, discussions from cluster group meetings. Mindful that initial teacher education can only start new teachers on the trajectory toward expert teaching (Anthony, Haigh, & Kane, 2011; Anthony & Kane, 2008), we wanted to understand more about how well our prospective teachers were prepared for and supported in their new roles in the workplace, in terms of implementing ambitious teaching practice.
Theoretical framework and design of intervention
Practice-based teacher education reforms
Practice-based (or -centred or -focused) approaches to initial teacher education involve placing teaching as a central element of learning to teach; the goal is to support prospective teachers in learning how to use knowledge of teaching in action (Ball & Foranzi, 2009; Lampert, 2010). The practice-based teacher education movement has two significant strands: (1) the identification of core practices of good teaching that form the basis of teacher education curriculum as it relates to teaching in general and teaching and learning of specific school subjects such as mathematics; and (2) the use of a range of pedagogies of practice. Pedagogies of practice, as defined by Grossmann, Hammerness, and McDonald (2009), comprise three elements: representations of practice (e.g., video records of lessons or records of student work); decompositions of practice (e.g., identification of specific instructional practices such as talk moves); and approximations of practice (e.g., simulations of certain aspects of practice through activities such as role play and rehearsal).
Core practices
Grossman et al. (2009) were early advocates of moving the curriculum focus of initial teacher education from viewing teachers as decision makers and reflective practitioners—with a focus on knowledge and reflection— towards a curriculum “organized around core practices, in which knowledge, skill, and professional identity are developed in the process of learning to practice” (p. 274). Core practices, sometimes referred to as high-leverage teaching practices (Ball & Forzani, 2011), involve practices and routines that are believed to support high-quality student learning. More than a list of teaching practices, the focus has been on “routine aspects of teaching that demand the exercise of professional judgements” required in “the constant in-the-moment decision-making” within the classroom (McDonald, Kazemi, & Kavanagh, 2013, p. 378). Aimed to address the “problem of enactment” (Kennedy, 1999), a focus on core practices is an “attempt to weave together novices’ development of meaningful knowledge for teaching with their capacity to actually enact ambitious teaching in particular disciplines in the classroom” (McDonald et al., 2013, p. 379).
In critiquing the growing list of core practices within the practice-based teacher education literature, Zeichner (2013) warns that core practices need to be framed around an appropriate grain size. McDonald et al. (2013), arguing against the prescription of one set of core practices, contend that it is more important that the field develop “a common understanding of the concept of core-practice so that the concept itself might become a field-wide tool for the organization and implementation of practice-based teacher education initiatives” (p. 380). In looking to avoid a reductionist approach, Grossman et al.’s (2009) criteria for core practices provides a useful guide as follows:
- practices that occur with high frequency in teaching
- practices that novices can enact in classrooms across different curricula or instructional approaches
- practices that novices can actually begin to master
- practices that allow novices to learn more about students and about teaching
- practices that preserve the integrity and complexity of teaching
- practices that are research-based and have the potential to improve student achievement.
In addition, several practice-based teacher education proponents (e.g., Lampert et al., 2013; Timperley, 2013) argue that attention to adaptive expertise in the design of practice-based learning experiences is one way to avoid the focus on core practices serving to de-professionalise teaching. Adaptive expertise is a key teacher characteristic promoted in recent reforms in teacher education (see Aitken & Sinnema, & Meyer, 2013 and Timperley, 2013).
Our project took as its starting point those practices identified as the key to the principles and vision of ambitious mathematics teaching—most notably, pedagogical practices that place students’ mathematical thinking and reasoning at the centre of instruction and support equitable engagement of diverse learners in rich mathematical activity. As a research group, we define the principles associated with the ambitious mathematics teaching as follows:
- Students are sense makers.
- Teachers and students learn together; relationships become a resource for developing mathematical proficiency and identity.
- Ambitious instruction requires clear mathematical learning goals.
- Teachers plan equitable and responsive learning experiences that enable each student to engage in rigorous academic mathematics work.
- Teachers plan mathematics learning experiences that enable students to build on their existing proficiencies, interests, and experiences.
Pedagogies of practice
McDonald et al. (2014) argue that conceptual coherence in practice-based teacher education reforms requires more than reorganisation of the curriculum around core practices or a specific vision of teaching such as social justice or reflective practice. Reforms need to take care to ensure that the “what” is inextricably linked to the “how” of teacher education. That is, making practice a central resource for learning requires changes in teacher education pedagogy itself. Describing it as a “sea change”, McDonald et al. (2013) suggest that this change “requires scholars and practitioners (often one and the same) to collaborate in the development of a common language for describing (a) how teachers learn to practice and (b) the pedagogies teacher educators enact to support teachers in learning to practice” (p. 381). In moving away from an acquisition model of learning associated with the theory–practice divide dilemma these researchers argue that initial teacher education could more usefully organise learning around a “cycle of learning to enact core practices that are strongly grounded in a situated perspective on learning” (p. 381) (see Figure 2) that embraces learning as a collective and social activity (Wenger, 1998).
Integrating Grossmann et al.’s (2009) classification of pedagogies of practice and core practices, the cyclic model can be applied to multiple settings—be they controlled (methods class), designed (methods and school based) or authentic (school). In our study, practice-based teacher education was trialled in some programmes in a controlled setting only and in other programmes in a designed setting.
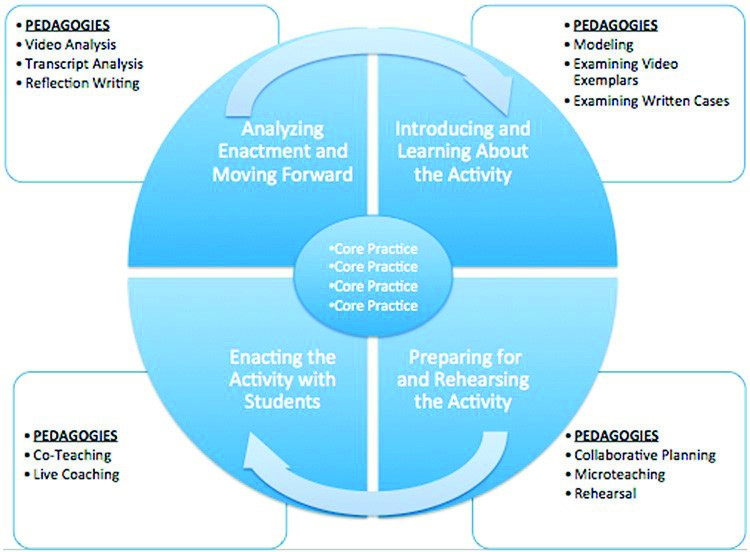
Figure 2: cycle for collectively learning to engage in an authentic and ambitious instructional activity
(McDonald et al. 2013, p. 382)
Overview of our course design: Designed setting
In designing our new pedagogical and curriculum interventions, we took our lead from the seminal Learning in, From, and For Teaching Practice (LTP) practice-based teacher education study (see Kazemi, Franke, & Lampert, 2009; Lampert & Graziani, 2009; Lampert et al., 2013). Their practice-based approach organised opportunities for prospective teachers to engage in “approximations of practice” (Grossman et al., 2009, p. 238) activities within a cycles of enactment and investigation (see Figure 3.) A key innovative feature of the design was prospective teachers’ engagement in public rehearsals with mathematics teacher educators’ coaching. in reviewing the teacher learning within their project, Lampert and colleagues (2013) found that pressing (through coaching interactions) the rehearsing prospective teachers to consider what they were doing in relation to aspects of practice or the underlying principles of ambitious mathematics teaching supported engagement in theory building and development of shared conceptual framework aligned to adaptive expertise.
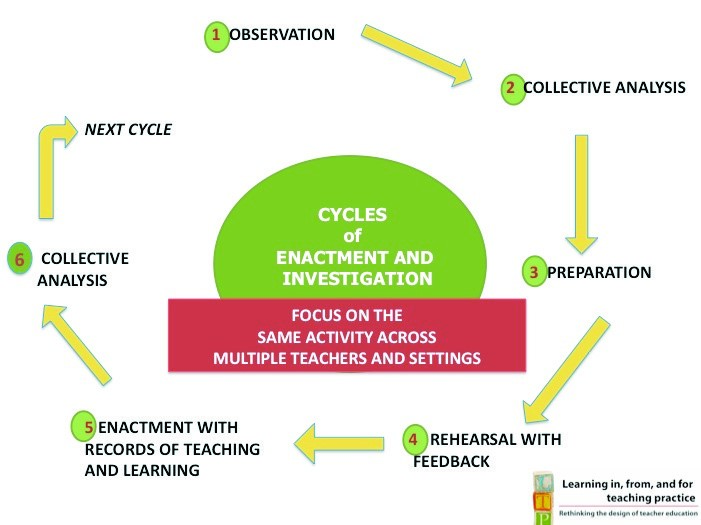
Figure 3: LTP model of cycles of enactment and investigation
Instructional activities
In the first stage of the intervention, we trialled a range of instructional activities within a public rehearsal process (Phases 1–4 of the LTP model). The instructional activities comprised classroom tasks that “structure the relationship between teacher and students around content in ways that consistently maintain high expectations of student learning while adapting to the contingencies of particular instructional interactions” (Kazemi et al., 2009, p. 12). They are designed to act as “containers” for the core practices, principles and mathematical knowledge associated with ambitious mathematics teaching.
Examples of instructional activities that we adopted from the LTP included quick images and choral counting.
Quick images, typically presented through a configuration of dots, are designed to engage students in visualising numbers and forming mental representations of a quantity. After briefly viewing the image students are asked to explain how they organised and subitised quantities in order to calculate the total number of dots in the image.
Choral counting involves the whole class/group counting together by some increment (e.g., 5, ½ or 0.2), forwards or backwards, while the teacher writes the count in a particular configuration of rows and columns on the board. The teacher stops the count at strategic points for students to discuss patterns emerging in the count, make predictions using those patterns, and/or explain why the patterns are occurring.
Other instructional activities that we used included strings, launching a problem, sharing solutions (instructional activities that can be found in wider use) and instructional activities developed and trialled within individual programmes within the project. These included: kanikani, an activity that involves the design of a dance sequence based on cultural performances (e.g., kapahaka, siva, sasa, hura, hula, ballet) through reference to geometric transformations; and patterns associated with algebraic expression of patterns such as Fibonacci sequence.
In Phase 1 of the enactment and investigation cycle, mathematics teacher educators modelled the teaching of the instructional activity with a group of prospective teachers acting as the learners. This modelling/observation phase provided opportunities for the “representation” and “decomposition” of practice (Grossman et al., 2009). Because the act of modelling “teaching” was not a familiar activity for most of the researcher/teacher educators, we chose to collectively practise and critique our modelling/teaching of each instructional activity within our research team (and some members chose also to practise teaching the instructional activities within local school settings).
We trialled different ways of modelling, including a single mathematics teacher educator modelling the teaching of an instructional activity followed by reflective discussion of practice, and modelling with in-the-moment coaching by a second mathematics teacher educator. in the latter case, the modelling of a rehearsal was initially used to illustrate how in-the-moment coaching would be used within prospective teacher-led rehearsals of practice. However, the activity of modelling with in-the-moment coaching was in itself found to be a useful way to engage prospective teachers in discussions about mathematics teaching practices. This approach was frequently adopted for programmes where it was unrealistic to provide multiple rehearsal times for prospective teachers (see Averill, Anderson, Drake, 2015).
Rehearsals
Rehearsals of instructional activities took place in two different settings—university mathematics methods courses and school-based settings. each setting was designed to enable the prospective teachers to teach mathematics to peers or children under conditions of controlled complexity and get feedback from peers or teacher-educators or teachers in partner schools. An important element of the preparation for public rehearsals was the scaffolded and collaborative planning opportunities and the establishment of community norms of participation.
School enactments
In the second and third years of the project, several of the mathematics methods courses, and a classroom inquiry course, were adapted to include Phases 5 and 6 of the cycle of enactment and investigation (see Figure 3). for each school visit, prospective teachers collaboratively planned the teaching sessions (involving an instructional activity or an instructional activity and a rich group task), and one or two prospective teachers taught a group of children (between 2 and 8 times dependent on the course). Peers of the prospective teachers observed each of the teaching episodes (videoed) and contributed towards group- and whole-class reflective activities. in addition, some courses were adapted to include assessment activities related to practise of instructional activities within the practicum teaching experience.
Findings
Focus 1 concerning the design of the instructional activities has been discussed above. in this section we present summary findings to date concerning our experience of enacting the design, the learning of practice by the prospective teachers during and after the initial teacher education experience, and we conclude with our reflections on our own learning and professional development as mathematics teacher educators.
Enacting the design: A focus on rehearsals and coaching
Firstly, in developing and enacting new pedagogies around rehearsals, we were surprised at both how much we needed to learn and at how much we learnt. As noted above, modelling effective teaching of instructional activities was a new activity for mathematics teacher educators and the experience sharply focused our attention on the identification of core practices around professional noticing of students’ thinking and positioning of students, all the while attending to the big ideas of mathematics.
Experimentation with modelling and coaching within rehearsal
The limitations of course contact time prompted us to experiment with various ways of incorporating modelling and coaching moves within rehearsals. As noted above, some courses adapted the modelling phase to include a second mathematics teacher educator acting as coach, to highlight core practices explicitly. Also groups of mathematics teacher educators experimented with the nature of coaching interactions—be they directive or open questions, prompts for discussion, or retrying teaching exchanges. An analysis of the use of coaching interactions applied across three programmes of study at Victoria University of Wellington (Averill, Drake, Anderson, & Anthony, 2015) explored the deliberate use of coaching exchanges initiated using open questions (in comparison to high frequency of directive coaching exchanges reported in Lampert et al.’s 2013 study). It was found that using questions, rather than giving an instruction about what next to do, ask, or say, enabled the presenting prospective teachers to explain their pedagogical decision making and maintain control of their teaching, while opening up the possibility of pedagogical discussion. For example, in the following exchange the question invites the presenting prospective teacher to consider other options:
| Coach: | Is there a way you can get the class talking a bit more, or did you not want them to? |
| Presenter: | No, I just wanted to get the numbers out and I didn’t want to put anybody on the spot. |
In instances such as this, both the coach and class were able to comment or offer ideas in relation to the presenter response, and the presenter had the opportunity to seek feedback on her pedagogical decision or to continue as planned. In this particular episode the question afforded an opportunity for the coach, presenter, and class to discuss suitable “talk moves” (Chapin & O’Connor, 2007) to promote mathematical talk. The exchange also illustrates that promoting learner talk is situated within the complexity of pedagogical decision making (in this case, maintaining the momentum of the activity and attending to perceived student confidence to participate), rather than in isolation.
Other exchanges involved inviting the presenting prospective teacher to share the rationale behind a particular teaching move. for example, in the following exchange, the presenting prospective teacher is prompted to explain why she chose a student to report an incorrect solution:
| Coach: | You obviously did some thinking about why you chose this specific response. can you share that? |
| Presenter: | I’m really trying to get students to think and share in pairs and to realise that they don’t always have to have the right answer, but that their thinking is work in progress. I wanted to give them the opportunity, iI thought maybe when they were explaining it, they might have thought, “oh, I know what it is now, it is meant to be such and such”. |
Using the open prompt also provided opportunities for involving other prospective teachers in the exchanges, thus maximising the potential learning opportunities afforded by time constraints. For example, in the following exchange we see how the coach question directed to all prospective teachers brought practices to the surface that aligned with sequencing student responses within a discussion report-back:
| Presenter: | I saw some really good work. Helen or Hamish, please could one of you come up to the board and show us your thinking for the next two lines? |
| Coach: | [to all] So how do you think Delia (presenter) made a decision about who to invite up to the board? |
| Hamish: | She saw that I hadn’t written any of the work. I had contributed ideas but I hadn’t written anything. |
| Coach: | I thought there might be a strategic mathematical reason? |
| Helen: | She recognised that we knew the strategy. she doesn’t want us coming up if we are going to get it all wrong. |
| Presenter: | That’s part of it; with my Year 9 class I would have picked the weakest overall pair who got it right—they are the ones not used to being good at maths, so that was why. You were right, I had seen you got it right, but I gave you the choice of Helen or Hamish. |
Following the sharing of the rationale related to formative assessment information (about a student’s written mathematical argumentation) and choosing someone who knew a solution method, we see how the discussion opened up opportunities to also discuss the importance of positioning the particular student as a successful mathematics learner, encouraging the student’s mathematical autonomy. Importantly, the wider discussion enabled the coach to evaluate the prospective teacher’s understanding of practice and highlight further practice-based links with coursework and course materials. In this case, the coach affirmed the presenter’s positioning of the lower achiever as “achieving” and highlighted the consistency of the presenter’s rationale with Stein et al.’s (2008) practices, discussed earlier in the course.
Supporting the learning of professional noticing of students’ mathematical thinking
Instruction that values and respects all students’ mathematical thinking, that places students’ mathematical thinking and reasoning at the centre of decision making, is at the heart of mathematics reforms. Developing communities of mathematical inquiry in which students learn to explain and justify their thinking, communicating with and responding to the arguments of others, requires rich discourse-intensive practices centred on the creation of robust learning opportunities for students to be oriented to peers’ ideas and to the big ideas in mathematics (Hunter, 2008). We, along with others (e.g., Ball & Forzani, 2011; Sherin, Jacobs, & Philipp, 2011) argue that the need to attend to, interpret, and respond appropriately to students’ mathematical thinking is a core pedagogical skill that needs to be consciously taught in any teacher preparation programme. Analysis of a series of rehearsal opportunities within a range of mathematics methods courses (Anthony, Hunter, Hunter, 2015) explored how the rehearsal process afforded for prospective teachers to practise and learn about how to listen and respond to students’ mathematical thinking. Multiple analytic passes of the videotapes resulted in the following categorisation of three broad categories related to instances of professional noticing episodes: making students’ thinking visible, eliciting and responding to student thinking, and encountering dilemmas.
We found that rehearsals occasioned multiple opportunities for prospective teachers to learn “about” and “how to” interpret a students’ explanation and to practise how to make student explanations accessible to other members of the listening community through the use of talk moves and recordings of students’ thinking. For example, in the following episode of a quick image activity (see Figure 4), the mathematics teacher educator pauses the rehearsal on several occasions to highlight ways to unpack the students’ thinking and make it more accessible to other students in the group.

Figure 4: Quick image
We pick up the rehearsal with Karl’s explanation for the count of 12 dots:
| Karl: | I saw a square and I went two, two, two, two and that was eight and then I went around the corners and added the rest. |
| Coach: | So Pam [presenting prospective teacher] this would be a good time to say to Karl, “so how did you get to eight?” Because now you want to know, because she is saying two, two, two, two, but how do you suddenly get to eight so you want to clarify that. |
| Pam [presenting prospective teacher]: | Yeah okay, so you went, which twos did you go? These two? [goes to image and indicates middle dots]. |
| Karl: | Okay so I saw the top two in the middle [presenting prospective teacher points to dots]. And then the two at the sides. |
In this instance, the coaching actions provided the rehearsing prospective teacher and other members of the community with real-time opportunities to see the effect of students being helped to make clear and accessible mathematical explanations. Following the coach’s prompting and modelling, the rehearsing prospective teacher took the opportunity to rewind her teaching and incorporate this new instructional move. The result was that Karl offered a clarification of his original mathematical explanation that made his reasoning more visible to other listeners.
Supporting the learning of culturally responsive teaching
Equity is not visible simply in what teachers do but also in the meanings and principles that guide how they view their learners, the relationships they build with learners, and the stance they take on the work of teaching. in particular, teaching in ways responsive to the cultures of our students is vital to enhance equity of access to achievement (Banks & Banks, 2010; Gay, 2010). However, despite a specific focus in New Zealand education policy (e.g., Ministry of Education, 2011, 2013), developing culturally responsive teaching and adopting culturally linked competencies has proven to be challenging (Bishop, 2012; Hynds et al., 2013). As, such, we were concerned as to how practice-based teacher education would assist prospective teachers to develop those cultural competencies associated with enhancing equity of access to achievement in the mathematics classroom. Initial analysis (see Averill, Anderson, & Drake, 2015) of cultural competencies associated with teachers’ “knowing, respecting, and working with Māori learners and their whānau and iwi so their worldview, aspirations, and knowledge are an integral part of teaching and learning” (Ministry of Education, 2011, p. 4) focused on “wānanga” and “ako”. Wānanga, is described as “participating with learners and communities in robust dialogue for the benefit of Māori learners’ achievement” (p. 4) and ako, as concerning teachers “taking responsibility for their own learning and that of Māori learners” (p. 4).
Analysis of the modelled rehearsals, in which one mathematics teacher educator “coached” another presenting mathematics teacher educator, confirmed how the processes inherent in modelling and decomposition of practice could usefully provide opportunities to develop prospective teachers’ capacity to professionally notice culturally responsive teaching in action. Wānanga was evident through the coach modelling how the teacher could talk with learners about their learning and through listening to their ideas. Ako was exemplified through examples of the reciprocity of teaching and learning, as seen in the following episode where the presenting mathematics teacher educator showed himself as being a learner by using trial and error and restarting the instructional activity. The instructional activity was a string that started with 20 litres of juice being put into 4-litre containers. The prospective teacher students were asked to decide what type of operation was needed to solve the problem, to discuss with their groups, and then to share their thinking with the class. After some sharing of mathematical ideas, the presenter paused:
| Presenter: | One of my problems at the moment with my string is that there is some mathematics going on here which is problematic for me running the string activity, and that is the whole business about whether this is a sharing problem or a repeated subtraction problem, and I was hoping that once I got a few more things up on the board I might be able to clarify what it is around here [points to the board] that would set the problem up as a particular type of problem … I was hoping that by using colour on the board, I would be able to pull the ideas together and back to the string, but my string activity is getting derailed. … |
| Coach: | So given we wanted to introduce using strings and the time is running out … |
| Presenter: | Then this isn’t a good example to start with! (laughter) … [to the class]. Remember i said that we were learning as we went through and did this? i haven’t done a string ever before, and I looked one up in a research article which was supposed to work. |
| Student: | Is the class context the issue? Is the problem that we are all preservice teachers and we’ve been told to look at every problem really flexibly and think of as many ways to solve a problem as we can? |
| Coach: | Yes, that might be the problem. |
| Presenter: | Let’s start again! [proceeds as a division problem and goes straight on to the second question in the string: 20 litres, this time being put in 2-litre containers, how many containers are needed? Then on to 1-litre containers, then ½-litre containers … the rehearsal progresses smoothly]. |
In this episode, the prospective teachers were able to hear and discuss the presenter’s rationale regarding why he felt the activity was not working as intended, then experience the activity again, this time presented in a different (and more successful) way. Prospective teachers’ knowing their teacher was not giving up on their learning, along with the positive classroom climate and relaxed laughter, is an example of ako in action.
Another aspect of ako is teachers being committed to high expectations of student learning. Many examples illustrating this aspect of ako were present in the rehearsals; learners were expected to engage with mathematical activities, and think about, share, listen to, and discuss mathematical ideas. Moreover, high expectations were modelled by presenters and coaches: it was expected that prospective teachers would be able to relate theory to practice and take part in pedagogical discussions as they participated in mathematical activities, even though it was mathematics that some found challenging.
Prospective teachers’ learning within and after their initial teacher education experience
Perceptions of learning within rehearsals
In addition to our analysis of learning opportunities around specific points of focus, we also collected data of prospective teachers’ perceptions of the rehearsal process by means of course surveys and post-rehearsal interviews. This data set indicated that prospective teachers were, for the large part, supportive of the rehearsal processes, inclusive of support for the planning process and in-the-moment coaching. concerning planning, typical responses to the need to anticipate student responses to the instructional activity included:
- It forced me to consider possible questions that students may ask. it forced me to break down mathematical concepts into manageable sized problems.
- It forced me to think about possible strategies that some students may use and how i was going to deal with them.
In terms of the rehearsal process, prospective teachers remarked on the value of “overcoming anxiety in a safe environment” and that:
- It was good to be able to stop and ask at a point if it was a good idea to do this or that;
- It was useful to see others at work, for one thing it was comforting to see others make mistakes and to see we are all learners even the lecturers.
These responses exemplified the community and collaborative-based norms that were associated with the structure of the rehearsals. This support was further exemplified in views about the coaching process, with responses such as:
- Stopping at certain points and being critiqued as I was going helped as it discussed right there and then.
- These discussions and comments were great as they allowed us all to learn from and with each other in a supportive environment.
- [There were] different viewpoints on how to do things and being able to work together and also debate which method or strategy would work more effectively.
- [It] allowed us to go deep into mathematical concepts and explore possible misconceptions.
Importantly, the instructional activities acted as “boundary objects” (Venkat & Adler, 2009) in that they bridged the rehearsal work in the university with the work in the classroom. Using the common language and understandings developed in the university rehearsal phase, prospective teachers were able to reflectively engage with the complexity of the teaching process. For example, in addition to the more pragmatic aspects of teaching such as voice pitch, writing on the board, and so on, the prospective teachers reported that the rehearsal process supported deep reflective engagement with learning the work of teaching. As prospective teachers noted:
- It made me think more deeply about my teaching as I had to answer questions such as “why did you do that?”
- Getting asked why you are doing something because it makes you reflect “in the moment” so you can remember exactly what you were thinking and why.
Developing adaptive expertise
The overall learning of prospective teachers is complex to measure and describe within any programme of study. One measure of learning that held particular interest in relation of learning the work of ambitious mathematics teaching was the development of adaptive expertise. Using the analysis framework proposed by Timperley (2013), we examined the development of expertise as characterised by shifts in teacher focus from self to student and from simple to increasingly complex understandings about teaching and learning. The prospective teachers in question, for the analysis to date, participated in the mathematics methods paper and a self-selected mathematics classroom inquiry option within their classroom inquiry paper (see Anthony, Hunter, & Hunter, 2015). Drawing on data from their journal reflections and pre- and post-course interviews, we argue that the instructional dynamics linked to practice-based pedagogies within our teacher education programme, inclusive of opportunities to experiment, risk-take, and engage directly with learner outcomes, supported the development of prospective teachers’ professional stance aligned to adaptive expertise. The teaching as inquiry model used within the classroom inquiry option pressed prospective teachers to link teaching actions to student learning. The individual and group reflective activities not only exposed their preconceptions, but also prompted them to analyse and rework their preconceptions as localised theories of teaching. In particular, our classroom inquiry module, with its focus on teaching and learning rich mathematical collaborative group tasks, disrupted prospective teachers’ everyday understandings of ability group work organisation (and associated fixed ability mindset) provoking (re)thinking about the role of students’ participation in sense-making in the mathematics lesson. We concluded that the key elements of the classroom inquiry module design that supported our prospective teachers’ development of adaptive expertise included the cyclic inquiry process focused on core practices of ambitious mathematics teaching—most notably the noticing and responding to students’ thinking, the use of research-based literature and frameworks to support evaluation and links to student learning outcomes, the opportunity to practise in a safe learning environment, and the support of the learning community established through collaborative practice-based activities (e.g., group planning and public rehearsals).
Transitioning to the classroom: Year 1 teachers
In addressing focus 4, our interest was whether the evidence of developing adaptive expertise would transfer into the classroom, combined with the concern about just how ambitious is ambitious mathematics teaching for the beginning teacher? This study involved a purposeful and self-selected sample of three beginning secondary teachers in the Wellington area and a cluster of six primary teachers who taught in the Manawatu/Hawke’s Bay and Auckland regions. The study was considered exploratory in nature, and it was not our intention to make causal claims about the effect of the intervention. Rather, we wanted to expand our own understanding about the teacher learning trajectory a part of our (re)consideration of our initial teacher education role in this journey. This concern was also driven by the paucity of exemplary ambitious teaching practices that prospective teachers reported observing during practicum. Typical responses in our classroom inquiry module interviews about the nature of group work were:
- It’s always been ability-based small group work and I’ve seen no whole-class math discussions.
- I haven’t really seen this kind of teaching … what I’ve seen is just a lot of grouping for grouping sake without the things behind it that make it make sense. So I’ve seen lots of teachers good at questioning, at eliciting individual student’s thinking and responses but haven’t seen that more students supporting students and working together yet.
The teachers were observed (videoed) in their mathematics classroom in Term 2 and 3 and completed post-lesson interviews focused on their preparedness for and experiences in mathematics teaching within the workplace. following each classroom observation round, two cluster group meetings facilitated by researchers/ teacher educators were organised for the primary teachers. Cluster group meetings provided opportunities for teachers to share their experiences, and collectively engage in professional dialogue and activities related to expressed challenges and directions in their learning to do the work of ambitious mathematics teaching.
What did we find?
The first round of classroom observations revealed differential levels of enactment of ambitious teaching practices as judged by the researcher observers. However, despite apparent differential levels in capabilities, what became apparent with this self-selected cohort was the strong commitment to continue to learn more about how to engage students more actively in mathematical sense-making in ways that positioned them as competent mathematicians.
We used the cluster meeting involving the primary cohort to explore links with teacher learning and their initial teacher education experience. Year 1 teachers’ identification of useful learning included:
- content knowledge
- identification of specific strands (e.g., statistics)
- pedagogical content knowledge
- awareness of importance of sound teacher knowledge for interpreting students’ thinking (value of errors, misconceptions)
- role of tools and representations
- differentiated task design
- core practices
- launching a problem (relevancy to students’ interest and current understanding)
- sharing strategies within a learning community (norms, helping others, individual and collective learning, positioning students as competent)
- eliciting and responding to students’ thinking (e.g., talk moves, questioning, building on students’ thinking)
- problem solving (engaging students, mathematical practices, mathematical argumentation)
- arranging for learning
- belief that each student can learn mathematics (flexible grouping practices, risk taking, removing fear of failure, focus on process rather than answer)
- making mathematics relevant (connecting to the real world).
We were also interested to explore perceived shortcomings of the initial teacher education experience: Did these prospective teachers learn things that they now perceived to be unhelpful, or were some crucial learning areas missed? While no unhelpful aspects were raised, the teachers questioned whether the length of the course was sufficient in terms of expectations of new learning associated with ambitious teaching practices. In the post-lesson 2 interview, one prospective teacher, Shelley, acknowledged the ongoing challenges associated with the complex and uncertain enterprise of ambitious teaching. For example, in whole-class discussion, she felt that she needed to “work on the ‘big mathematical connect’ because I feel that I get wrapped up in what they are doing halfway through—yeah it’s just making sure I’ve done the planning to make sure I can sequence and I know I want to come out at the other end.” However, Shelley noted that a big advantage of this approach was that listening to students provided an important resource for getting her own “content knowledge up to scratch, and that’s coming through the planning as well”. As Bray (2011) notes, those teachers with “sound knowledge are more apt to notice and respond to critical learning moments in the lesson, and are more likely to be able to use students’ thinking as springboards for inquiry in the context of class discussions” (p. 35). for Shelley and others, we saw further evidence of generative teacher learning practices in the form of teacher records of students’ thinking. Shelley remarked: “writing everything down that the students come up with, and I take their ideas and revisit them after the lesson and then go okay, what’s the lower level strategies and what’s the higher level strategies and where do I need to be heading them.”
Suggested areas of increased focus included:
- assessment tools (Junior Assessment of Mathematics, National Standards benchmarking against the New Zealand curriculum documentation)
- classroom task or activities/websites
- facilitating learning in mixed ability groups, plus collaborative learning, plus rich discussions
- behaviour management (expectations of students managing their learning independently of the teacher, higher level learning)
- ways to cope with differences between their own and their teaching team’s priorities in relation to mathematics teaching approaches. For example, with reference to numeracy, one prospective teacher was concerned about “how to tick off strategies to be learnt in inquiry maths” (when other classes are not using an inquiry maths approach).
The collection of data across the transition from initial teacher education to the classroom also enabled us to consider the effect of instructional activity rehearsal in terms of enactment of ambitious pedagogies. To date, we have analysed one beginning teacher’s enactment of a quick image starter (see Anthony, Hunter, Hunter, & Duncan, submitted 2015). Providing numerous examples of the principles and practices of ambitious mathematics teaching, the analysis confirmed that for this teacher—Shelley—ambitious teaching was a realistic option. Shelley had established a vibrant community of learners who were mathematically engaged and active sense-makers. Efforts to maintain high-level cognitive demands were particularly evident in Shelley’s resistance to breaking down the task into smaller steps that relied on “following” teacher demonstrations. Instead, she stayed true to her students’ thinking at all times and supported them to connect their prior learning to new learning. Moreover, in line with adaptive expertise, Shelley’s professional noticing of her students’ mathematical thinking enabled her to continually adapt the lesson to promote the engagement, learning, and well-being of each of her students. A feature of her attention to student thinking was the use of discussions to support collaborative analysis and revision of the flawed solutions, which in turn provided multiple opportunities for students to revisit and think more deeply about a range of underlying mathematics concepts. Aligned with our belief that effective teaching depends on one’s capacity to learn from and in practice, we are confident that Shelley’s focus on her students’ mathematical thinking, her belief that mathematics is a learning subject rather than a performing subject, her enactment of dynamic assessment practices, and her generative inquiry stance, will contribute to her ongoing development as an ambitious mathematics teacher.
Mathematics teacher educators’ learning and professional development
The project involved us as mathematics teacher educators changing and critiquing our practice. Mathematics teacher educator learning was supported by engagement with expertise (research literature, international and local colleagues’ input) and engagement within a learning community (our research team).
The inquiry-based framework (design research) enabled the continuous development of our expertise trajectories in that we grew more aware, more curious, and more informed about our role and the processes of learning the work of teaching. insights into how we might design and enact practice-based teacher education and enhance understanding about ambitious mathematics teaching shaped what we each bought to rehearsals. For example, midway through the project, our “aha” moments included:
I’m a learner as well: in modelling the instructional activities, I was charged with enacting high-leverage practices in a visible and “expert” way. After modelling, there was a public opportunity to review the instructional activity enactment. I was challenged to justify my actions in terms of evidence about what worked (or didn’t) and why and what alternatives and changes might be possible. In being prompted to think more deeply about how I was occasioning opportunities to learn within a group, with an explicit focus of attending/listening to and building on each learner’s thinking, the realisation of the power of a community of learners in relation to equitable practice was a significant outcome for me. Just as students and teachers in the classroom should be co-learners of mathematics, this pedagogical approach supports teacher educators and prospective teachers to be co-learners of ambitious mathematics pedagogy.
Who is getting to practise: The thinking we had been doing in the maths team about rehearsal suddenly leaped out at me—it shouldn’t be the just the facilitators who were learning to lead practical activities better, it should be the teachers we are working with. We have turned things around, moving away from a modelling approach where we hoped that teachers would note what we as facilitators did to support learning, to one where each teacher has opportunity to lead a practical experience multiple times. We are working on ways to help them as they repeat an activity with a series of groups to: anticipate and note ways round common difficulties, note actions and questions that promote fruitful discussion, focus learners on the key aspects of the experience and generally develop their discourse management skills.
Importantly, the rehearsal provided a direct and explicit window into understanding the nature and progress of prospective teachers’ learning that we had not previously experienced. In addition to direct observation of teaching capability and progress, the rehearsals enabled us to: (a) seek clarification/elaboration about a prospective teacher’s rationale for a specific instructional move, and (b) seek peer and/or provide direct input on suggestions concerning dilemmas of practice—most notably associated with erroneous responses and issues of student engagement. As such, we were more able to adapt our instruction and provide support in terms of where to next, in ways that were responsive to the diverse learning needs of prospective teachers.
Conclusions and implications for teacher education
Our collective vision was that the practice-based opportunities to learn the work of ambitious mathematics teaching in the university and school setting would occasion prospective teachers’ learning in ways that supported them to continue to learn in and from their practice. In doing so, we hoped that they would develop those attributes of professionalism associated with inquiry, collective responsibility, and knowledge co-construction that signify adaptive expertise—expertise that is crucial for mathematics teachers to “do teaching that is more socially and intellectually ambitious than the current norm” (Lampert et al., 2013, p. 241). Only when we see this happen will we make sustained progress in countering the systemic levels of underachievement and disengagement for many learners in the mathematics classroom.
We found that:
- The use of practice-based pedagogies focused on rehearsal of instructional activities was beneficial in highlighting core practices that underpin ambitious mathematics teachings.
- Rehearsals were particularly effective at engaging prospective teachers in professional noticing practices (e.g., building on students’ thinking and cultural competencies) associated with learning to teach diverse students.
- Implementation of practice-based teacher education, while both possible and beneficial, requires that changes in curriculum focus and assessment practices be integrated with changes in pedagogies.
- Rehearsals provided opportunities for prospective teachers to learn to do the work of ambitious mathematics teaching, in ways that were not currently afforded through the majority of their practicum experiences.
- A “teaching as inquiry” approach explicitly supported the development of a trajectory of adaptive expertise capability.
- While first year teachers differed in their enactment of ambitious teaching practice, the vision of those who engaged in further research was strongly aligned to reforming practice and a trajectory of growth in expertise.
- The use of practice-based pedagogies changed our focus as mathematics teacher educators from considerations of prospective teachers’ (and our own) teacher quality to teaching quality, and that teaching quality was more firmly connected to supporting diverse learners and equitable practices.
- Teacher educators needed space/time and collaborative support to learn new pedagogies and to develop adaptive expertise associated with enacting responsive pedagogies.
In addition, we noted that our findings in progress have informed the promotion of practice-based teacher education and associated goals of adaptive expertise development as detailed in Timperley’s (2013) position paper on teacher education reforms, and have also informed the design of the large-scale Pasifika success professional learning project led by Associate Professor Hunter.
Knight et al. (2014) argue that while the field of teacher preparation has made modest strides towards developing a professional knowledge base, “we know little about the learning, practices, and preparation involved in ‘teacher educator’ education” (p. 268). This TLRI project has confirmed for us the value of collaborative exploration to learn new ways of working and being. opening our practice up to the scrutiny of peers was at times confronting and challenging, but always rewarding.
Our findings offer a challenge to strong calls for prospective teachers to spend considerably more time in the field—in looking for a third space (Zeichner, 2010), the approximation of practice afforded by the pedagogies of rehearsal and subsequent enactment in school settings (e.g., in designed settings in course inquiry modules) offers an alternative way for developing pedagogies of enactment that support prospective teachers to learn the work of teaching while placing the teacher educator in contexts where they can learn from and with their prospective teachers.
Limitations and future research
While we dabbled in an exploration of what the prospective teachers take from practice-based teacher education, there is much more to learn about how the cycle of enactments within our design allow them to take up ambitious teaching practice in their practicum experiences and beyond. We agree with Grossman and McDonald’s (2008) call for “studies of teacher education that can track the impact of programmes over time while respecting the complexity of linking initial preparation to eventual outcomes” (p. 199). There are currently too few studies that investigate how preparation influences prospective teachers’ practice, especially with regards to enabling them “to navigate the complex task of teaching increasingly diverse populations in the face of strong accountability pressures” (Cochran-Smith et al., 2015, p. 117). In particular, we need to build on this research to look specifically at the development of adaptive expertise (Anthony et al., in press)—viewed as essential in order to minimise the possibility of beginning teachers’ socialisation to the more familiar transmission modes of mathematics teaching. We also need research on the effects of particular mixes of teachers’ characteristics, school context, and practice-based teacher education features (Cochran-Smith & Villegas, 2015).
While cognisant that within the current climate of teacher education reforms and accountability, the problem of creating forms of practice-based teacher education that are too complex and or costly to implement and sustain are ever pressing (Zeichner, 2013), we think that there is much to learn about the value of practice-based teacher education. Forzani (2014) suggests three characteristics that differentiate this approach to acquisition of focal characteristics of teaching as follows:
- the learning goals for students target higher order skills
- teaching in this manner is partially improvisational so prospective teachers need to learn to deal with uncertainty
- the subject matter of the practices is a critical component of the acquisition of the practices.
With point number three, we are more convinced than ever, that learning to teach mathematics requires specialist teaching skills and knowledge that requires dedicated space within teacher education programmes. Our collective engagement in this study has helped us re-vision our mathematics teacher education programmes, and we hope that it provides an impetus to others, across a range of curriculum areas, to join the practice-based teacher education movement.
Publications from this project
Anthony, G., Hunter, J., & Hunter, B. (2015). Prospective teachers developing adaptive expertise. Teaching and Teacher Education, 49, 108117.
Anthony, G., Hunter, J., & Hunter, R. (2015). Learning to professionally notice students’ mathematical thinking through rehearsal activities. Manuscript submitted for publication.
Anthony, G., Hunter, R., Hunter, J., & Duncan, s. (2015). How ambitious is ‘ambitious mathematics teaching’? Manuscript submitted for publication.
Anthony, G., & Hunter, R. (2013). Learning the work of ambitious mathematics teaching. in V. steinle, L. Ball & c. Bardini (eds.), Mathematics education: Yesterday, today and tomorrow (Proceedings of the 36th annual conference of the Mathematics education Research Group of Australasia, pp. 699–702). Melbourne, Vic: MeRGA.
Anthony, G., & Hunter, R. (2012). (Re)thinking and (re)forming initial mathematics teacher education. New Zealand Journal of Educational Studies, 47(1), 145–151.
Averill, R., Drake, M., & Harvey, R. (2013). Coaching pre-service teacher for teaching mathematics: The views of students. in V. Steinle, L. Ball & c. Bardini (eds.), Mathematics education: Yesterday, today and tomorrow (Proceedings of the 36th annual conference of the Mathematics education Research Group of Australasia, pp. 707–710). Melbourne, Vic: MERGA.
Averill, R., Anderson, D., & Drake, M. (2015, submitted for publication). Developing culturally responsive teaching through professional noticing within teacher educator modelling.
Averill, R., Drake, M., Anderson, D., & Anthony, G. (2015). The use of questions within in-the-moment coaching in initial mathematics teacher education: Enhancing participation, reflection, and co-construction in rehearsals of practice. Manuscript submitted for publication.
Hunter, R., Hunter, J., & Anthony, G. (2013). using instructional activities to learn the work of ambitious mathematics in pre-service teacher educator settings. in V. Steinle, L. Ball & C. Bardini (eds.), Mathematics education: Yesterday, today and tomorrow (Proceedings of the 36th annual conference of the Mathematics Education Research Group of Australasia, (pp. 703–706). Melbourne, Vic: MERGA.
Presentations Conferences and Workshops
Anthony, G. (2013, June). Learning, in, from, and for practice. Paper presented at the institute of education Research seminar series, Massey University, Palmerston North.
Anthony, G., & Averill, R. (2014, 10 July). Learning the work of ambitious mathematics teaching. Paper presented at the Ako Aotearoa/ Teaching & Learning Research Initiative Research in Progress Colloquium IV, Wellington.
Anthony, G., Hunter, J., & Hunter, R. (2014, July). Prospective mathematics teachers’ adaptive expertise. in S. Oesterle, C. Nicol, P. Liljedahl, & D. Allan (eds.), Proceedings of the joint meeting of Psychology of Mathematics Education 38 and PME-NA 36 (Vol. 6, p. 9). Vancouver: PME.
Averill, R., Drake, M., Anderson, D., & Anthony, G. (2014, Dec). Promoting ambitious teaching: Using questions within in-the-moment coaching in initial teacher education. Paper presented at the speaking back through Research AARE-NZARE 2014 Conference, Brisbane, Australia.
Averill, R., Drake, M., Anderson, D., & Anthony, G. (2014). Promoting ambitious teaching: Using questions within in-the-moment coaching in initial teacher education. Paper presented at the faculty of education seminar series Victoria University of Wellington.
Drake, M., Anderson, D., & Averill, R. (2015, April). Exploring productive pedagogies for teacher education: Developing wānanga and ako in rehearsals with coaching. Paper presented at the faculty of education seminar series. Victoria University of Wellington.
Hunter, J. (2012). Learning the work of ambitious mathematics teaching. Paper presented at the collaborative Action Research network Palmerston North.
Hunter, R. (2013). Instructional activities as a way to support diverse learnings access to classroom talk. invited workshop, Canterbury University, Christchurch.
Hunter, R., Hunter, J., Anthony, G., Averill, R., Drake, M., Harvey, R., & Rawlins, P. (2012, Dec). Learning the work of ambitious mathematics teaching. Paper presented at the annual conference New Zealand Association of Educational Research, Waikato.
Rawlins, P., Anthony, G., Hunter, R., Averill, R., Drake, M., & Hunter, J. (2013, Dec). Pedagogies of practice in initial teacher education settings: Strengthening links between coursework and fieldwork. Paper presented at the NZARE conference and annual meeting, Dunedin.
Rawlins, P., Averill, R., Anthony, G., Hunter, R., Drake, M., & Hunter, J. (2014, Dec). Pedagogies of practice: Strengthening links between coursework and fieldwork in initial teacher education. Paper presented at the speaking back through Research, the AARE-NZARE 2014 Conference, Brisbane, Australia.
References
Aitken, G., Sinnema, C., & Meyer, F. (2013). Initial teacher education outcomes: Standards for graduating teachers. University of Auckland. Retrieved from www.educationcounts.govt.nz/publications/ECE/2511
Alton-Lee, A., Hunter, R., Sinnema, C., & Pulegatoa-Diggins, C. (2011). BES Exemplar1: Developing communities of mathematical inquiry: Retrieved from http://www.educationcounts.govt.nz/goto/Bes.
Andreotti, V., & Major, J. (2010). Shifting conceptualisations of knowledge and learning in initial teacher education in Aotearoa/New Zealand. Journal of Education for Teaching, 36(4), 441–459.
Anthony, G., Haigh, M., & Kane, R. (2011). The power of the ‘object’ to influence teacher induction outcomes. Teaching and Teacher Education, 27(5), 861–870.
Anthony, G., Hunter, J., & Hunter, B. (2015). Prospective teachers developing adaptive expertise. Teaching and Teacher Education, 49, 108-117.
Anthony, G., Hunter, J., & Hunter, R. (2015, submitted for publication). Learning to professionally notice students’ mathematical thinking through rehearsal activities.
Anthony, G., & Hunter, R. (2012). (Re)thinking and (re)forming initial mathematics teacher education. New Zealand Journal of Educational Studies, 47(1), 145–151.
Anthony, G., Hunter, R., Hunter, J., & Duncan, s. (2015). How ambitious is ‘ambitious mathematics teaching’? Manuscript submitted for publication.
Anthony, G., & Kane, R. (2008). Making a difference: The role of initial teacher education and induction in the preparation of secondary teachers: Final TLRI report. Wellington: NZCER.
Anthony, G., & Walshaw, M. (2006). Numeracy practices and change. (Teaching and Learning Research Initiative Report). NZCER. Retrieved from http://www.tlri.org.nz/pdfs/9201_finalreport.pdf
Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best evidence synthesis iteration [BES]. Wellington: Ministry of Education.
Averill, R. (2012). Caring teaching practices in multiethnic mathematics classroom: Attending to health and well-being. Mathematics Education Research Journal, 24(2), 105–128.
Averill, R., Anderson, D., & Drake, M. (2015). Developing culturally responsive teaching through professional noticing within teacher educator modelling. Manuscript submitted for publication.
Averill, R., Drake, M., Anderson, D., & Anthony, G. (2015). The use of questions within in-the-moment coaching in initial mathematics teacher education: Enhancing participation, reflection, and co-construction in rehearsals of practice. Manuscript submitted for publication.
Ball, D., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special. Journal of Teacher Education, 59(5), 389–407. doi: 10.1177/0022487108324554
Ball, D. L., Ben-Peretz, M., & cohen, R. B. (2014). Records of practice and the development of collective professional knowledge. British Journal of Educational Studies, 62(3), 317–335.
Ball, D. L., & Forzani, F. M. (2009). The work of teaching and the challenge for teacher education. Journal of Teacher Education, 60(5), 497–511. doi: 10.1177/0022487109348479
Ball, D. L., & Forzani, F. M. (2011). Teaching skillful. Educational Leadership, 40–45.
Banks, J. A., & Banks, C. A. M. (eds.). (2010). Multicultural education: Issues and perspectives (7th ed.). Hoboken, NJ: John Wiley.
Bishop, R. (2012). Pretty difficult: implementing kaupapa Māori theory in English-medium secondary schools. New Zealand Journal of Educational Studies, 47(2), 38-50.
Chamberlin, M., & Caygill, R. (2012). Key finding from New Zealand’s participation in the Progress in International Reading Literacy Study (PIRLS) and Trends in International Mathematics and Science Study (TIMSS) in 2010/11. Wellington: Ministry of Education
Chapin, S. H., & O’Connor, c. (2007). Academically productive talk: supporting students’ learning in mathematics. in w. G. Martin, M. Strutchens & P. Elliot (eds.), The learning of mathematics (pp. 113–139). Reston, VA: NCTM.
Cochran-Smith, M., & Villegas, A. M. (2015). framing teacher preparation research: An overview of the field, Part 1. Journal of Teacher Education, 66(1), 7–20.
Cochran-Smith, M., Villegas, A. M., Abrams, L., Chavez-Moreno, L., Mills, T., & stern, R. (2015). critiquing teacher preparation research: An overview of the field, Part ii. Journal of Teacher Education, 66(2), 109–121.
Confrey, J. (2006). The evolution of design studies as methodology. in R. k. sawyer (ed.), The Cambridge handbook of the learning sciences (pp. 135–151). Cambridge: Cambridge University Press.
Education Workforce Advisory Group. (2010). A vision for the teaching profession. Wellington: Ministry of Education.
Ell, F., & Grudnoff, L. (2012). The politics of responsibility: Teacher education and “persistent underachievement” in New Zealand. The Educational Forum, 77(1), 73–86. doi: 10.1080/00131725.2013.739023
Forzani, F. M. (2014). Understanding “core practices” and “practice-based” teacher education: Learning from the past. Journal of Teacher Education, 65(4), 357–368.
Gay, G. (2010). Culturally responsive teaching: Theory, research, and practice (2nd ed.). New York: Teacher College Press.
Ghousseini, H., & Herbst, P. (2014). Pedagogies of practice and opportunities to learn about classroom mathematics discussions. Journal of Mathematics Teacher Education, 1–25.
Gravemeijer, K., & Cobb, P. (2006). Design research from a learning design perspective. in J. van de Akker, K. Gravemeijer, S. Mckenney & N. Nieveen (eds.), Educational design research (pp. 17–51). London: Routledge.
Grossman, P., Hammerness, k., & McDonald, M. (2009). Redefining teaching, re-imagining teacher education. Teachers and Teaching: Theory and Practice, 15(2), 273–289.
Grossman, P., & McDonald, M. (2008). Back to the future: Directions for research in teaching and teacher education. American Educational Research Journal, 45(1), 184–205. doi: 10.3102/0002831207312906
Hammerness, K., Darling-Hammond, L., & Bransford, J. (2005). How teachers learn and develop. In L. Darling-Hammond & J. Bransford (eds.), Preparing teachers for a changing world (pp. 358–389). San Francisco: Jossey-Bass.
Hunter, R. (2008). Facilitating communities of mathematical inquiry. In M. Goos, R. Brown & R. Makar (eds.), Navigating currents and charting directions. Proceedings of the 31st annual Mathematics Education Research Group of Australasia conference (Vol. 1, pp. 31– 39). Brisbane: MERGA.
Hunter, R., & Anthony, G. (2011). Learning to “friendly argue” in a community of mathematical inquiry (Teaching and Learning Research Initiative Report). Wellington: New Zealand Educational Research Council.
Hynds, A., Meyer, L. H., Penetito, W., Averill, R., Hindle, R., Taiwhati, M., . . . Faircloth, s. (2014). Evaluation of He Kakano: Professional development for leaders in secondary schools 2011–2012. Wellington: Ministry of Education.
Kazemi, E., Franke, M., & Lampert, M. (2009). Developing pedagogies in teacher education to support novice teachers’ ability to enact ambitious instruction. in R. Hunter, B. Bicknell & T. Burgess (eds.), Crossing divides: Proceedings of the 32nd annual conference of the Mathematics Education Research group of Australasia (pp. 11–29). Wellington: MERGA.
Kennedy, M. M. (1999). The role of preservice teacher education. in L. Darling-Hammond & G. sykes (eds.), Teaching as the learning profession: Handbook of teaching and policy (pp. 54–86). San Francisco, CA: Jossey Bass.
Kilpatrick, J., Swafford, J., & Findell, B. (eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Lampert, M. (2010). Learning teaching in, from, and for practice: What do we mean? Journal of Teacher Education, 61(1–2), 21–34.
Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., & Franke, M. (2010). Using designed instructional activities to enable novices to manage ambitious mathematics teaching. in M. K. Stein & L. Kucan (eds.), Instructional explanations in the disciplines (pp. 129–141). New York: Springer.
Lampert, M., & Graziani, f. (2009). Instructional activities as a tool for teachers’ and teacher educators’ learning. The Elementary School Journal, 109(5), 492–509.
Louden, w. (2010). 101 damnations: The persistence of criticism and the absence of evidence about teacher education in Australia. Teachers and Teaching, 14(4), 357–368.
McDonald, M., Kazemi, E., & Kavanagh, S. S. (2013). Core practices and pedagogies of teacher education: A call for a common language and collective activity. Journal of Teacher Education, 64(5), 378–386.
McDonald, M., Kazemi, E., Kelley-Petersen, M., Mikolasy, K., Thompson, J., Valencia, S. W., & Windschitl, M. (2014). Practice makes practice: Learning to teach in teacher education. Peabody Journal of Education, 89(4), 500–515.
Ministry of Education. (2011). Tātaiako: Cultural competencies for teachers of Māori learners. Wellington, New Zealand: Ministry of Education.
Ministry of Education. (2013). Ka Hikitia–Accelerating success 2013–2017: The Māori education strategy. Wellington, New Zealand: Ministry of Education.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: NCTM.
National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: US Department of Education.
New Zealand Teachers Council. (2010). Approval, review and monitoring processes and requirements for initial teacher education programmes. Wellington: Author.
Santagata, R., & Yeh, C. (2014). Learning to teach mathematics and to analyze teaching effectiveness: evidence from a video-and practice-based approach. Journal of Mathematics Teacher Education, 17(6), 491–514.
Sherin, M., Jacobs, V., & Philip, R. (eds.). (2011). Mathematics teacher noticing. New York: Routledge.
Stylianides, G. J., & Stylianides, A. J. (2014). The role of instructional engineering in reducing the uncertainties of ambitious teaching. Cognition and Instruction, 32(4), 374–415.
Thames, M., & Zoest, L. (2013). Building coherence in research on mathematics teacher characteristics by developing practice-based approaches. ZDM, 45(4), 583–594.
Timperley, H. (2013). Learning to practise: A paper for discussion. university of Auckland. Retrieved from www.educationcounts.govt.nz/ publications/schooling/2511/learning-to-practise
Venkat, H., & Adler, J. (2008). expanding the foci of activity theory: accessing the broader contexts and experiences of mathematics education reform. Educational Review, 60(2), 127–140.
Wenger, E. (1998). Communities of practice: Learning, meaning and identity. Cambridge: Cambridge University Press.
Young-Loveridge, J. (2010). A decade of reform in mathematics education: Results for 2009 and earlier years. In Averill, R., Bicknell, B., Bonne, L., et al (Eds.), Findings from the New Zealand Numeracy Development Projects 2009 (pp. 15–35). Wellington: Learning Media. Retrieved from http://nzmaths.co.nz/annual-research-and-evaluation-reports-and-compendium-paper
Zeichner, K. (2010). Rethinking the connections between campus course and field experiences in college- and university-based teacher education. Journal of Teacher Education, 61(1–2), 89–99.
Zeichner, K. (2012). The turn once again toward practice-based teacher education. Journal of Teacher Education, 63(5), 376–382.



