Making mathematical thinking visible

1. Mathematical parts and wholes

Of all the subjects in the New Zealand school curriculum, mathematics is perhaps the most strongly associated in students’ minds with expectations of conformity, accuracy, and rule-following. Yet mathematicians describe mathematics as a source of intense aesthetic pleasure, creativity, and play (Lockhart, 2009; Sinclair, 2004). Chevallard (as cited in Eisenberg & Dreyfus, 1991) attributes this difference to “didactical transposition”, a process whereby academic mathematical knowledge is broken down and sequentially ordered into atomistic units that are easy to teach and assess. As a result of this transposition, students often experience instructional mathematics as components or building blocks: small, explicitly presented pieces of knowledge and skills to be mastered via carefully calibrated exercises.

A more holistic view sees mathematics as complex structures comprising intricate and profoundly useful webs of relationships (Shapiro, 1997). Such a perspective is rarely offered in standard textbook presentations of mathematics that emphasise exercise sets within compartmentalised content areas. Rather, this holistic view is more accessible through alternative tasks that feature modelling (Lesh & Doerr, 2003), investigations (Mason, Burton, & Stacey, 1982), problem solving (Schoenfeld, 1985), and problem posing (Kontorovich, Koichu, Leikin, & Berman, 2012), and which encourage students to struggle with the interconnectedness of mathematical structures by creating complex, often contextually situated, mathematical products. Yet alternative mathematical tasks are seldom implemented in many upper-secondary and tertiary mathematics classrooms in New Zealand, but are dismissed by teachers, decision makers, and even students, with the remark, “These are fun problems, but where’s the maths?”.

Our research project grew from wondering why these tasks appear less mathematical to stakeholders than sets of exercises. We saw two contributing factors. First, student mathematical activity in these alternative tasks is usually messier, less predictable, and more prone to error than in traditional exercise sets—a byproduct of exploring complex, interconnected structures, rather than learning its piecemeal components. Second, these alternative tasks are well known for addressing a range of mathematical competencies that traditional exercise sets typically do not, such as mathematical communication, collaboration, critical thinking, and creativity (DeBellis & Goldin, 2006; Maaß, 2006)—so-called “soft skills” whose value in enacted (and even intended) curricula often comes second to mathematical content. We posited that the more risk-averse education becomes (Biesta, 2015), the more these alternative tasks become known for supporting “soft skills” that can be itemised on lists of learning outcomes. As with traditional exercise sets, these alternative tasks may become valued more for the skills they encourage students to develop than for the messy, complex, risky mathematical structures those students create and manipulate using those skills.

We chose to view this situation as a problem of communication. Could we develop better ways of communicating the complex mathematical activity generated by students exploring mathematical structures holistically? Doing so might help stakeholders to recognise the mathematical value of alternative mathematical tasks and integrate them more meaningfully into mathematics education settings in New Zealand.

2. Risky mathematising tasks

Rather than attempting to cover the entire range of alternative mathematical tasks on offer, our project focused on a particular class of tasks that we designed, which we are beginning to call risky mathematising tasks.

An example of one such risky mathematising task is “The Jandals Problem” (Yoon, Moala, & Chin, 2016). The task begins with some warm-up questions that familiarise students with diagrammatic representations of graphs (networks) within the context of friendship associations, where a node represents a person, and an edge between two nodes represents a friendship between two people. After the warm-up questions, a scenario is posed: Xanthe, an American exchange student in New Zealand learns that locals use the word jandals to refer to what she commonly calls flip-flops. Upon returning home, Xanthe wants to spread the word jandals throughout different networks of friends like the one shown below in Figure 1. Students are asked to:

Create an algorithm (method) that Xanthe can use to figure out the first person whom she should share the word with first in each friendship network to ensure that the word gets passed on to everyone in the network as rapidly as possible. She assumes that a person will share the word with all of his/her friends on one day, and each of those friends will share it with their friends the next day. Ensure that your algorithm will work for any friendship network, not just the one given [Figure 1]. (Yoon et al., 2016, p. 12)

Only Figure 1 was initially given to the students; other friendship networks were given to them (one after the other) in later parts of the session.

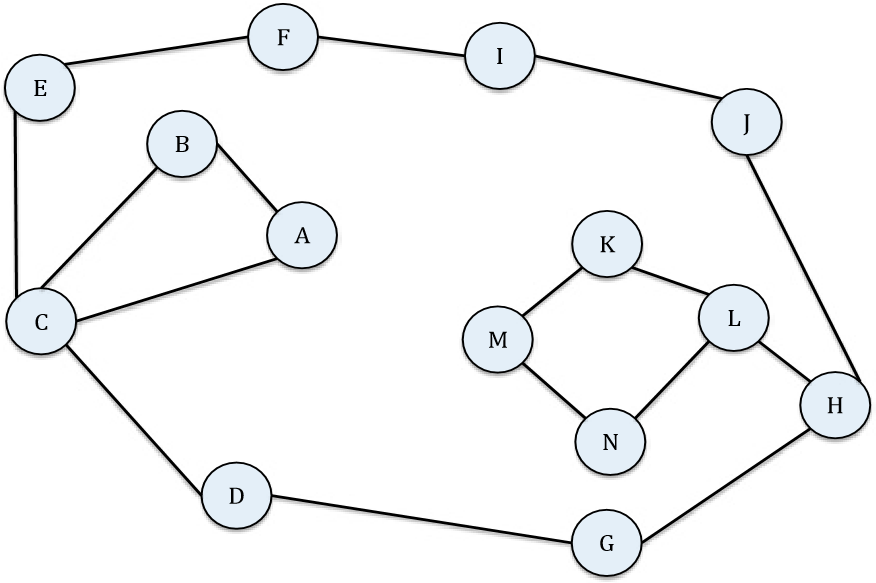
Figure 1: Friendship network 1 for the jandals problem

The jandals problem is representative of the suite of five risky mathematising tasks that we designed and used in our project (see Yoon, Chin, Moala, & Choy (2018) for another example).

We use the term mathematising in the sense of Freudenthal (1968) and Treffers (1987) to refer to the act of interpreting a situation mathematically. One can mathematise a real-life situation (or even a purely mathematical situation) by translating relevant objects, relationships, patterns, conditions, and assumptions into mathematical terms (Lesh & Doerr, 2003; Niss, Blum, & Galbraith, 2007). As we anticipated few students would be drawn into mathematising a purely mathematical situation, we deliberately designed our tasks around contexts we thought were imaginable and relatable (Pfannkuch & Budgett, 2016) to students. Our tasks were designed in consultation with six senior secondary school students from two decile 1 schools, and begin with local contexts such as a tug of war competition on school athletics day, a startup tourism company for North Island attractions, and seating arrangements in a Manukau foodcourt. The tasks invite students to work in teams of two or three for 50 minutes to create and communicate a team mathematical product (such as an algorithm, arrangement, or argument) that will help an imagined client (e.g., Xanthe in the case of the jandals problem) navigate through their problematic situation (e.g., wanting to know who to share the word “jandals” with first in any friendship network).

The term risky is taken from Biesta (2015), who criticises the attempts of policy makers, politicians, and the public to control and mechanise education by making it “strong, secure, predictable, and risk-free” (p. 1). Biesta argues that education is inherently risky, being at heart a dialogical process, an “encounter between human beings”, that “only works through weak connections of communication and interpretation, of interruption and response” (p. 1) and that removing the risk from education is effectively removing education altogether.

Our mathematising tasks are risky for students who must create an original mathematical product through mathematising a challenging, complex, and novel situation. Rather than trying to reduce this risk by making the problem smaller or giving hints to ensure students get the “right” solution, we encourage students to struggle, take wrong turns, and get stuck. The goal is not for students to get the right answer, but to become sufficiently entangled in the mathematical structures they create while making sense of the situation that they experience the structures as interconnected systems, seeing them from the inside out as it were. In fact, in most of these tasks, there is no perfect mathematical solution. Typical progress looks messy, slow, and frustrating as students challenge and revise their initial mathematisations as they notice flaws and new relationships, with occasional (and seemingly unpredictable) bursts of pleasure when they see some structure in a new way. The tasks are also risky for teachers, who cannot anticipate and plan for all the ways students may approach the problem. This riskiness is an inevitable byproduct of students creating their own situated mathematical structures, which mimics the kind of risky (also thrilling and addictive) activity that mathematicians regularly engage in.

To amplify the risk factor even further, we chose to focus these tasks on discrete mathematics (Hart & Sandefur, 2017), a relatively new field of mathematics which is ever-growing in prominence due to its significance in computer science and the many real-world applications of its sub-branches (e.g., probability, logic, combinatorics, and cryptography). Discrete mathematics focuses on objects with separate, distinct (often integer) values, in contrast to topics like calculus that involve continuous objects such as the change in a car’s speed. The jandals problem is set within the discrete mathematics context of networks, which explores systems of relationships (e.g., friendships) between distinct objects (e.g., people). Being relatively new, discrete mathematics does not feature prominently in the school curriculum and, therefore, school students have encountered little discrete mathematics in their schooling. Embedding our tasks in the field of discrete mathematics means that students are unable to fall back on pre-learned rules and algorithms, but must mathematise their own.

Our conceptualisation of these alternative tasks as risky mathematising tasks is one of the products of our project, and marks a shift in the development of these tasks over two previous projects as model-eliciting activities (Yoon, Patel, Radonich, & Sullivan, 2011) and conceptual readiness tasks (Barton, Davies, Moala, & Yoon, 2017).

3. Research questions

Our research was motivated by observations that educational stakeholders often fail to notice the complex mathematical activity generated by students exploring mathematical structures holistically. The overarching research question was:

How can we capture and describe student mathematical activity in a way that raises its visibility while retaining and respecting its complex nature?

The problem we perceived was that the mathematical activity of students during risky mathematising tasks is so complex that it is not immediately visible to students and educators. Our first sub-question addressed the need for effective forms of communication to highlight this complex mathematical activity to stakeholders.

1. What kinds of reports will document, measure, and describe the mathematical activity of students working on risky mathematising tasks in a way that makes this complex mathematical thinking visible to students, teachers, and decision makers?

We use the term “report” in its original sense, as something that carries (portare) back (re-) an observer’s account of a situation to others. We wanted to use our training as skilled mathematical observers to create reports that “carry back” our accounts of students’ mathematical activity to stakeholders, carefully highlighting the complex mathematical activity we see that may not be immediately visible to them.

We were conscious of wanting to preserve the complexity of students’ rich mathematical activity in our reports, and avoid simply creating more lists of mathematical components, such as processes, content, skills, knowledge, concepts, procedures, competencies, behaviours, or habits of mind. Our second sub-question addressed the need for theoretical tools to help us achieve this goal.

2. What theoretically grounded analytical framework can be used to capture and describe rigorously the complex mathematical activity of students working on risky mathematising tasks, in order to inform the design of practical reports?

4. Research design

We used a design-based research approach (Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003) to pursue our twin goals of developing practical reports and the theoretically grounded analytical frameworks supporting them. The project involved designing reports for students, teachers, and researchers, and full details of the research design can be found in Yoon et al. (2018).

4.1 Research setting and participants

Fifty-two student participants were recruited from a diverse range of instructional sites in New Zealand (see Table 1) that were purposefully chosen to enhance the generalisability of our results. Participants came from six mathematics courses in three educational sectors: secondary school, foundation studies (transitional programmes to prepare alternative pathways for students entering tertiary study), and undergraduate mathematics. The course contexts within each educational sector are further differentiated: the two secondary schools have different decile ratings; the two foundation studies programmes prepare students for different universities and degree programmes; and the two undergraduate mathematics courses cater for students with different majors. As data collection spanned 2 years, each course was offered at least twice, and students were drawn from a total of 13 distinct classes.

Table 1: Instructional settings from which student and teacher participants were recruited

		Site	Institution	Description of mathematics course (approx. class size)
Education Sector	Secondary	1	School A (decile 7)	Year 12/13 mathematics with calculus class (25)
		2	School B (decile 3)	Year 12 mathematics class (25)
	Foundation Studies	3	University C	Pre-degree bridging course in algebra (100)
		4	University D	Pre-degree bridging course in algebra (40)
	Undergraduate	5	University D	First-year undergraduate service mathematics course for nonmathematics majors (1,000)
		6	University D	Second-year undergraduate discrete mathematics course for mathematics and computer science majors (150)

Six teachers who taught in each of the courses partnered in the research (see Table 2). These teachers had a wide range of experience in using mathematics education research to inform their teaching, as well as differing motivations for participating in the project. This diversity enabled us to hear a range of challenging and sometimes conflicting perspectives on the artefacts designed, which encouraged us to test, examine, and revise them more robustly.

Table 2: Background information about teacher partners

Site	Teacher participant’s professional role	Mathematics education research experience	Motivation for participation
1	Secondary school mathematics teacher and HOD	Conducted MSc research in mathematics education	Wished to use modelling activities as internal assessment projects
2	Secondary school mathematics teacher and assistant HOD	Limited experience in education research	Open to experimenting with activities to engage students, and to help students gain the credits they need
3	Foundation studies mathematics lecturer and programme leader	Conducting PhD research in mathematics education	Wished to see how project can contribute to her teaching and research
4	Foundation studies mathematics lecturer and course co-ordinator	Conducted MPhil research in education	Open minded about value of mathematising tasks for raising student engagement
5	University lecturer and undergraduate co-ordinator in mathematics	Limited experience in education research	Wished to reflect on pedagogical practice and develop education research experience
6	University lecturer and research mathematician	No experience in education research	Open minded about relevance of mathematics education research to his teaching

4.2 Procedures and data collection

In order to design practical ways of reporting on students’ mathematical work, we first needed to engineer observable instances of such work. Therefore, we engaged student participants in two types of sessions: (1) risky mathematising sessions, to generate data on student mathematisations, and (2) report evaluation sessions, in which students experienced and evaluated reports of their mathematisations. Teachers were involved in separate report evaluation sessions.

4.2.1 Risky mathematising sessions: The students worked in 17 teams comprising two or three students from the same class. All participant involvement took place outside of class time and outside of course requirements. This allowed for high-quality data to be collected without classroom noise or interruptions and unaffected by course assessment concerns. Over the 2-year period, each team worked on up to four risky mathematising tasks for 60 minutes per task in the presence of a researcher who presented and clarified the task but did not offer mathematical hints. Students were video and audio recorded, and their inscriptions on paper were collected, along with researcher observation notes. A total of 57 hours of student mathematising activity was collected.

4.2.2 Report evaluation sessions: The form and delivery of the reports varied as the design evolved, but the same procedure was used to share the reports with the students and for the students to evaluate the reports. Once the reports were ready for each team, they were shared with the student team by a researcher(s). Students then evaluated the reports via questionnaires completed individually and group interviews. Closed items on the questionnaire invited students to judge the perceived accuracy, readability, and usefulness of the reports. Open items invited students to reflect on how they might use the information from the reports to prepare for future mathematics learning, and the similarity of these reports to other kinds of feedback they have received in their mathematics education. Group interviews followed a semi-structured interview protocol to probe their evaluations further, and to expand on how the reports might be improved. A total of 26 reports were shared and evaluated in this way.

4.2.3 Teacher report evaluation sessions: Reports of student work were also created for the six teacher partners, although they did not view work from their own students for ethical reasons, but learned about student work from other classes—both at the same educational sector and different sectors to provide comparison. The teacher partners experienced two sets of reports, one each year of the project, and evaluated the reports via individually completed questionnaires and individual or pair interviews, which followed a semi-structured protocol.

4.3 Design cycles

Although distinct sets of reports were created for students and teachers, the results from testing one kind of report naturally informed the subsequent designs on the other. Thus, we will describe here the evolution of the design cycles that took place with student reports, as well as how this evolution interacted with the design cycles that took place with teacher reports.

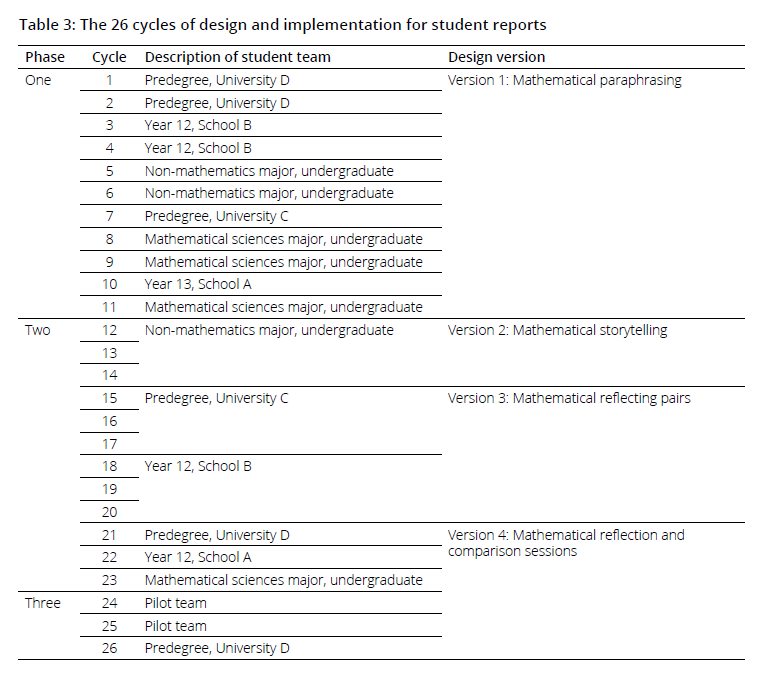
4.3.1 Student report design cycles: The reports of student mathematical activity for students were developed over 26 design cycles, which occurred in three distinct phases and are described in Table 3.

Phase one: Rapid prototyping (11 cycles over 9 weeks): The first phase used rapid prototyping (Joseph, 2004) to provide prototype designs based on our starting theoretical framework of SPOT diagrams^[1] (Yoon, 2015). Eleven reports were developed and shared with students over 9 weeks, with results from each test influencing the design of the subsequent report. Debrief sessions were held by designers on three occasions during the rapid prototyping, and results of student evaluations and designer debriefs were pooled at the end of phase one to inform our critique and refinement of our theoretical framework.

Phase two: Design and theory development (12 cycles over 30 weeks): More time (30 weeks) was given to the second phase, which comprised shorter sequences of design cycles (three cycles, then six cycles, then three cycles) interspersed between several sessions in which we critically examined and revised the theoretical groundings of our analytical framework. The design of our practical reports underwent two fundamental shifts during this time, informed by regular debrief sessions, student evaluations, and changes to our theoretical influences.

Phase three: Design sharability (3 cycles over 6 weeks): In the final phase, we focused on enhancing the sharability of our design and the practical knowledge of the researcher–designer team. We created detailed practitioner guides to describe how to create and implement the two components of our final design. We varied our roles and recruited a new researcher–designer–practitioner to test out and implement our guidelines over three cycles. During this time, the researcher–design team engaged in training to develop their competencies as reporting practitioners, in which they wrote practitioner reflections, practised mock sessions, and held detailed debriefing sessions with a counselling supervisor who could advise on the practitioner skills needed to conduct the “reflecting teams” component of the reports (described in Sections 5.1.3 and 5.2.1 of this report).

4.3.2 Interaction of design cycles for student and teacher reports:Reports of student mathematical activity for teachers were designed and tested over nine design cycles, which took place over 2 years, and interacted heavily with the 26 design cycles for the student reports. In the first year, the reports for teachers were significantly different in style from those shared with students, as they reported on multiple examples of student work and used short video stories to cover a wide range of student mathematising. The effectiveness of these videos with teachers led to them being embedded within the second version of the design for students (mathematical storytelling). The third version of the design for students (mathematical reflecting pairs) was then embedded within the second version of reports for teachers, while being augmented by additional reports on multiple examples of student work, which teachers were asked to compare. This contributed to the design of comparison sessions that were included in the fourth version of student reports. In this way, the reports designed for students and teachers developed symbiotically and synergistically.

5. Research findings

Design-based research is often so complex and involves so many cycles that many researchers struggle to report their findings, as there is “too much story to tell” (McKenney & Reeves, 2012, p. 202). This is certainly the case for us, and with 26 design cycles conducted in three phases over 2 years, we are still in the early stages of making sense of our findings. In this section, we share three types of findings:

1. The process of theorising, designing, and testing our product at the student level.
2. The final version of our reporting format (the practical product) at the student level.
3. Findings on student mathematical activity.

5.1 The process of theorising, designing, and testing our product

We wanted to help students become more sensitised to mathematical nuances in their own work, so they might notice new mathematical connections and possibilities they had not seen before, and produce mathematically enhanced algorithms, methods, and arguments. But we could not just command students to be more mathematically sensitive! We needed to design some intervention that could produce this learning phenomenon more organically. We chose to focus on designing a form of “report” rather than a teaching intervention, as the former could potentially be shared more widely than the latter, which would likely be shared with students only, and not with other stakeholders such as teachers and HODs. We describe how our understanding of the learning phenomenon we were trying to produce evolved through four versions of the design.

5.1.1 Version 1: Mathematical paraphrasing

paraphrase, v
trans. To express the meaning of (a written or spoken passage, or the words of an author or speaker) using different words, esp. to achieve greater clarity (OED online, 2018)

Our initial design attempt was to create verbal reports in which we “paraphrased” back to students the mathematics we saw them do, much like skilled therapists paraphrase their client’s comments back to them to demonstrate their interest in the client’s story, while creating opportunities for clarification and elaboration (Ivey, Ivey, & Zalaquett, 2014). In therapy, paraphrasing can help clients feel heard and respected, open up, and can even help them to see their own situation in a new way. This first version of our instructional design framed us as mathematical therapists, observing students’ mathematical activity then paraphrasing it back to them in a way that would hopefully help them to notice new mathematical connections and possibilities they had not noticed before.

Of course, there were many differences: skilled therapists paraphrase their client’s discourse frequently during a session in a back and forth exchange, whereas we offered one 40-minute paraphrasing session about 2 weeks after our first observation of their mathematical activity. The 2-week period gave us a chance to analyse the student work rigorously, using a modified version of the SPOT diagram approach (Yoon, 2015) to prepare detailed descriptions of the mathematical activity we had observed in students, using mathematical language that was appropriate and accessible to the students.

Most of the 32 students who experienced our paraphrasing sessions seemed to appreciate them: they were intrigued to hear about their thinking process, “It’s interesting to hear what you [the observer] found interesting”, and described the paraphrasing sessions as accurate and informative. In individual questionnaires, 90% of student participants described the reporting sessions as either “accurate” or “very accurate”; 87% described the reporting sessions as “useful (or very useful) for understanding the mathematics they had done”; 79% described the reporting sessions as “useful (or very useful) for preparing for future similar tasks”. Some students said the reports gave them a greater sense of agency—that they believed they would perform better if they attempted another similar task: “Next time I come to these kinds of problems I know what to do to do better.”

The students remarked that the reporting sessions were unlike anything they had experienced in their mathematics classes. This was not surprising, as each reporting session was the culmination of extensive analysis that is impossible to do under typical classroom teaching conditions—a point students readily acknowledged. Most of the feedback students reported having experienced in mathematics classes was limited to a “tick or cross”, which described the correctness of their final product, but overlooked their process. Many students appreciated that our reports focused on their process, saying they did “a much better job at exposing a lot of the reasoning behind my mathematical processes” and led them to think more about their own mathematics: the reports created “opportunities to think about something in a different way”.

Even more illuminating than these positive results of the testing were the few, significant negative responses from some students which, together with the unsustainable intensity of the data analysis, suggested the need for us to improve our design. In cycle seven, for example, one student objected to his paraphrasing report, saying that he felt it was harsh and made him feel like his potential had been limited. He said he didn’t want to be “stuck in a box”, yet acknowledged that the content of the report was “kinda true”. When the researcher acknowledged how difficult it was to give feedback, the student attempted to reassure her, saying, “Don’t take it personally, my missus always tells me I can’t handle the truth.”

In delivering our reports, we consciously strove to give clear, detailed descriptions of the mathematics we had observed without making students feel uncomfortable. We did this by avoiding evaluative comments, and focusing on sharing observations that we deemed fair, accurate, respectful, helpful, and interesting. Despite such efforts, the presenter of reports couldn’t escape a feeling of being “in the firing line”, especially when students reacted to feedback they perceived as critical. At the same time, the students were rarely actively involved in making sense of their work. The lengthy time given to analysis did not always lead to better stories, but often made it more difficult to choose what to tell them, and some of the most mathematically productive and enjoyable parts of the sessions occurred when the researcher responded to students’ spontaneous questions in the moment. We perceived the need to change the format of these reports to reduce this tension and to create room for students to reflect, question, and comment more meaningfully.

5.1.2 Version 2: Mathematical storytelling

While designing teacher reports, we created a suite of eight “video stories” in which we described episodes of student work that we considered structurally interesting examples of mathematisings (see Figure 2 for sample screenshots of these video stories). While reflecting on the shortcomings of our mathematical paraphrasing sessions, we realised that the video stories we had created for teachers could also be used in our reports for students. Showing video stories of other students’ mathematical approaches reduced the potential for confrontation caused by the direct address of mathematical paraphrasing sessions. The videos also addressed a request from some students to see examples of other students’ solutions to the tasks. But, most importantly, we anticipated that these stories about other students’ mathematical experiences would encourage students to reflect on and describe their own experiences, in the same way that storytelling begets storytelling from listeners and tellers alike (Clandinin & Connelly, 2000).

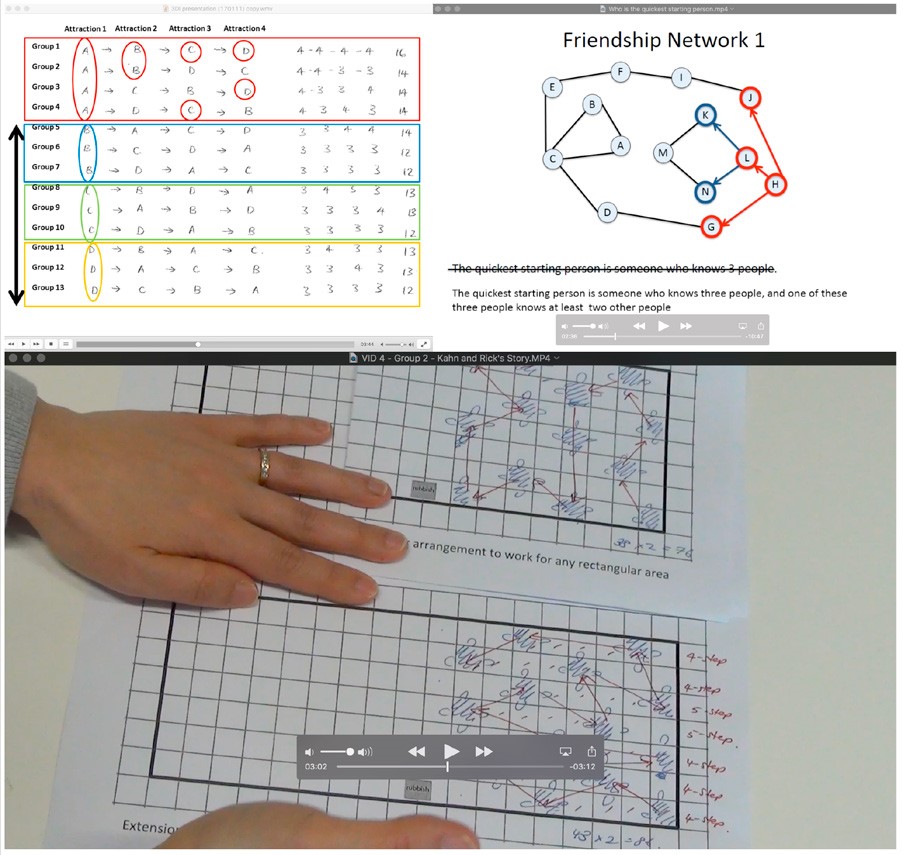
Figure 2: Screenshots from three “video stories” describing episodes of student work on risky mathematising tasks

As the video stories had already been created, we changed the timing of our reporting sessions (which we referred to as mathematical storytelling), holding them 10 minutes after students finished working on the risky mathematising task. We (the researchers implementing the mathematical storytelling sessions) became storytellers and librarians, locating the appropriate stories to suit the students depending on their mathematical performance on each task. We implemented the storytelling sessions three times with one group of students (cycles 12, 13, and 14 in Table 2), and expected to hear the students open up and tell their own stories as they noticed similarities and differences between the video stories they watched and the mathematising they had done themselves. The results were disappointing. The students said very little after viewing the video stories, and even appeared bored and detached when asked questions about these examples of other students’ work. On the other hand, when we asked them to explain what they had done for parts that had been inaudible or confusing to us as observers (as we didn’t have the benefit of time to analyse their thinking ourselves), they became visibly animated and discussed their mathematics, even noticing new mathematical relationships in the process. We realized that we had undertheorised (ignored, even) the impact of power dynamics in these reporting sessions: the students seemed most willing to make sense of their mathematical activity when they were in a position of agency, explaining something to us. This made sense, but didn’t seem to help with our design goal. We were committed to reporting, “bringing back” our own observations of the students’ mathematical activity, in order to highlight holistic, complex, structural aspects of their mathematising that they often did not realise they engaged in. Was such a goal still possible?

5.1.3 Version 3: Reflecting pairs

Our answer came in the unusual and unexpected form of an approach from family therapy practice, called “reflecting teams” (Andersen, 1987; Paré, 2016; White, 2000), which we adapted to structure our reporting sessions. This unique approach involves having a team of observers share their impressions in the presence of a family (or in our case, a student group), who listen to, but are not expected to respond immediately to, the observer’s conversation. After this conversation, the roles are reversed, and the family clients (student group) reflect through conversation on what they have heard, and what new ideas have emerged for them. In our first attempts to incorporate this format, we used pairs of reflecting observers, while our final version involved teams of three reflectors, one of whom also acted as the reflection leader as described in Section 5.2.

The reflecting teams approach offered a number of advantages over our previous versions. First, the indirect address (where conversations are conducted in the presence of students, but not directly addressed to the students) provides a formal structure for managing the power dynamic that can suppress conversation or reflection in more direct forms of address. Second, having more than one researcher conducting the reflections gives students an opportunity to observe the kind of attention we would like them to adopt. Namely, we encourage them to be respectfully attentive to their own mathematics, and approach it with an attitude of wonderment. Third, a diversity of interpretations are elicited in the reflecting teams which exposes students to multiple interpretations of their mathematical activity and encourages them to add their own which may build on, challenge, or align with those they have heard.

We were initially surprised by how well this format worked with our student participants and aligned with our goals, given its origin in the distant field of family therapy. Yet families are like teams of students creating original mathematical products in that they are both complex systems that cannot be reduced and understood in simplistic components. We also realised that the learning phenomenon we were trying to produce through these reporting sessions was similar to mathematical “revelation”, where students experience anew some mathematics that was already there before, but see it in a new way that is often surprising to them (Roth & Maheux, 2015). Thus, the reflecting teams’ design framework helps us to “engineer” the kinds of mathematical revelation learning our project is trying to understand.

5.1.4 Version 4: Mathematical reflection and comparison sessions

The final shift occurred after seeing the reflecting pairs format work well in six sessions to create a safe, structured environment in which students could acknowledge and appreciate their own mathematical work. By the end of a mathematical reflection session, student participants seemed sufficiently aware of and secure in their own mathematics to be ready to engage in a more critical examination of their mathematics, which would further enhance their mathematical sensitivity. Here, we were guided by literature on the value of comparison tasks in teaching and learning mathematics (e.g., Fraivillig, Murphy, & Fuson, 1999; Rittle-Johnson & Star, 2011; Stigler & Hiebert, 1999), and we designed mathematical comparison sessions in which students could compare their own mathematical solutions to those of others. The combination of mathematical reflection sessions and comparison sessions offers a balance between raising and directing students’ awareness of their own and others’ mathematics.

5.2 The final version of our design (the practical product)

Our final version of our design was a two-part session:

1. mathematical reflection session that aims to enhance students’ awareness of their own mathematical activity by inviting them to listen and respond to the conversations of mathematically skilled observers reflecting on their work
2. mathematical comparison session that seeks to deepen students’ critical appreciation of their own mathematical activity by comparing it to other mathematical approaches to the same task done by others.

5.2.1 Mathematical reflection sessions

The mathematical reflection sessions draw on the reflecting team approach in family therapy (Andersen, 1987; White, 2000), in which family members are exposed to conversations held by teams of skilled family counsellors reflecting on the family dynamics. Our translation of this approach to mathematical reflection sessions involves four stages which are represented in Figure 3.

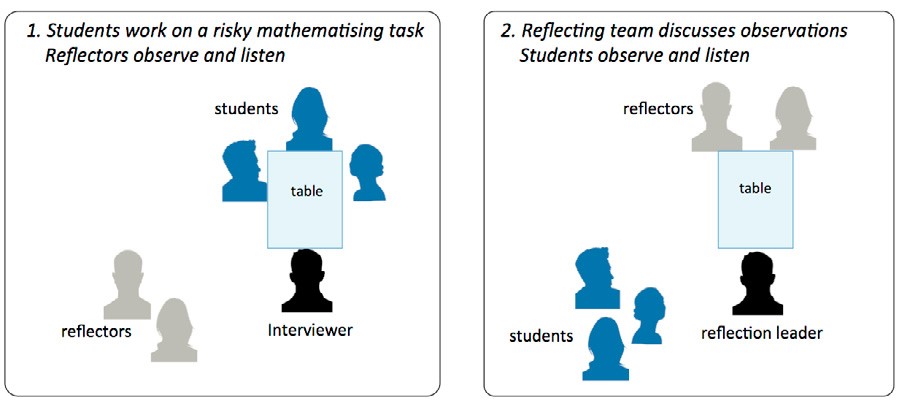
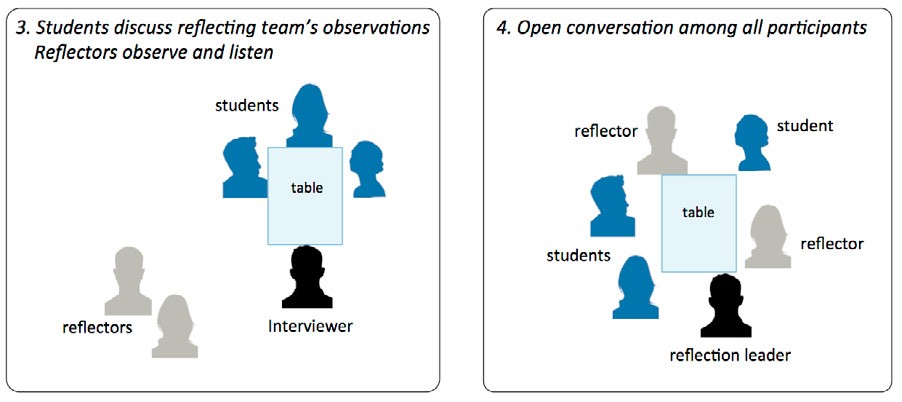
Figure 3: Four stages of interactions between participants during a reflection session

First, students complete a risky mathematising task (see 1 in Figure 3) in the presence of an interviewer and other reflectors who are trained in observing mathematical discourse, and who spend the session quietly observing and listening to the students’ activity.

Next, students swap places with reflectors, with reflectors taking their turn at the table to discuss their observations of the students’ mathematical activity, while students observe and listen quietly (see 2 in Figure 3). The reflecting team comprises the reflectors and the interviewer who leads the conversations as reflection leader, offering his or her own observations as appropriate. The reflecting team discussion centres around the following four questions (adapted from S. Penwarden, personal communication, 1 June 2017), which are designed to create space for acknowledgement and generativity (Paré, 2016) in reflectors’ mathematical noticings:

1. What was mathematical about what you noticed in [students’ names] work? What did you appreciate about it?
2. Where do you think newness or discovery turned up in [students’ names] work today?
3. What has observing [students’ names] work today got you wondering about?
4. Where or how might [students’ names] extend their thinking in working with this problem?

After students listen to this conversation, they once again swap places with the reflectors, and return to the table to discuss their reactions to the reflecting team’s observations about their mathematical activity (see 3 in Figure 3). The interviewer prompts student discussion by asking students the following four questions:

1. What struck you from the reflecting team’s discussion?
2. Where did something new emerge for you today?
3. What did you learn about how to work with the problem from hearing the reflecting team’s discussion?
4. What might you do differently in how you approach your mathematics learning?

During the student conversation, the reflectors again listen and observe, and refrain from offering clarification in order to allow the students to make sense of what they have heard in their own way. Finally, all students, reflectors, and the reflection leader come to the table for an open discussion where everyone is encouraged to share their perspectives on the conversation, and lines of communication are open between students and reflectors who can ask, clarify, and pursue new ideas together (see 4 in Figure 3).

5.2.2 Mathematical comparison sessions

Motivated by the extensive literature on comparison (e.g., Fraivillig et al., 1999; Rittle-Johnson & Star, 2011; Stigler & Hiebert, 1999), the mathematical comparison session provides students with the opportunity to attend more deeply to their mathematical product by comparing it with those of other students who have also worked on the task. The session involves only the reflection leader and the students. Ideally, the mathematical comparison session take place 1 day to 1 week after the mathematical reflection session, to give students enough time to digest what they have learned, but not too much time that they struggle to recall details of the reflection session. In our project, comparison sessions lasted for 100 minutes (with a 10-minute break in the middle), although shorter sessions are certainly possible.

Before the comparison session, members of the reflecting team meet to choose a suite of three to five examples of other students’ work to form the structure of the session. Care is taken to choose examples that vary in mathematical similarity to students’ work, including some that are very similar, and some that are significantly different and will extend the students mathematically. In our project, we created eight video clips that narrated “mathematical stories” about students working on the tasks that we found to be structurally distinct and interesting. We drew on these video stories as well as samples of students’ written solutions to the tasks when selecting our suite of examples (see Figure 4).

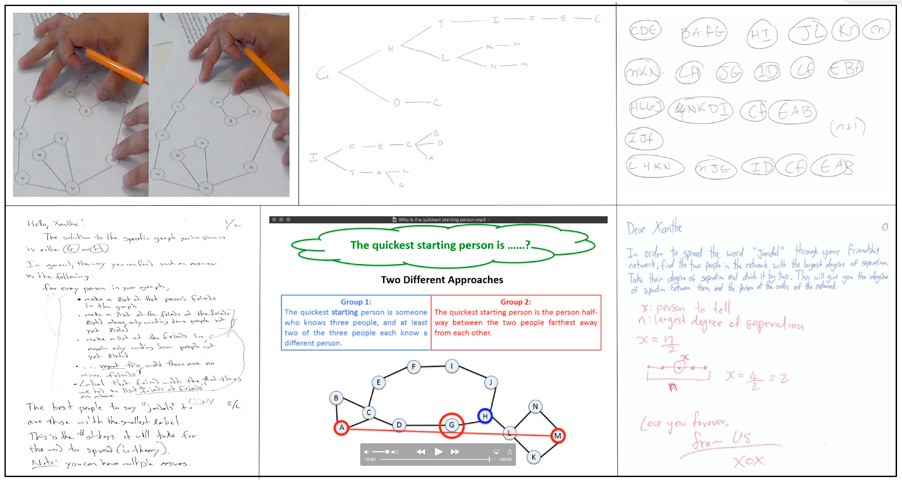
Figure 4: Six examples of students’ work used in a mathematical comparison session on the jandals task

The mathematical comparison session begins with the comparison leader showing an example that is very similar to the students’ own solution. Students are asked to read/view it, and then to answer two questions:

1. How is this team’s work (mathematically) similar to your work?
2. How is this team’s work (mathematically) different from your work?

Focusing on mathematical similarities can reassure students that other students also think the same way as them. It can also help strengthen students’ understanding of their own ways of thinking, which can help them make connections among alternative approaches (Maciejewski & Star, 2016). Asking students to identify mathematical differences can draw the students’ attention to variations in structures (Mason, 2003), enabling them to see how their own and others’ structures may be improved.

5.3 Findings on student mathematical activity

Our fine-grained analyses of students’ mathematical activity during the risky mathematising tasks yielded some findings on how students create and understand algorithms. An algorithm can be thought of as “a step-bystep set of instructions in logical order that enables a specific task to be accomplished” (Thomas, 2014, p. 36). Examples of algorithms include recipes for baking chocolate cake, and procedures for multiplying multi-digit numbers together. Creating algorithms is a central theme in discrete mathematics education research (Hart & Sandefur, 2017; Morrow & Kenney, 1998), and was a feature of two of our risky mathematising tasks, including the jandals problem described in Section 2.

We had anticipated that students would create an algorithm for the jandals problem by recalling and articulating the actual steps they took to find the solution for various scenarios. But the majority of the algorithms students created did not align with their procedures for finding solutions. It emerged that many students did not regard algorithms as a set of instructions, but as a pattern, a formula, an equation: something simple and concise. These simplistic conceptions of algorithm (as a formula or pattern) often led students to reject the “instruction-like” procedures they created because they did not take the form of equations or formulae. In some cases, these procedures were in fact primitive versions of the most mathematically efficient algorithms for the task at hand.

When students tested and refined their initial algorithm, we observed that some of their final algorithms preserved mathematically incorrect properties of the initial algorithm. For example, Table 4 shows four successive algorithms that one group developed for the jandals problem. The property of “sharing the word with someone who has three friends” is mathematically invalid but it is preserved in all four of the group’s algorithms.

Table 4: Four successive algorithms developed by one group for the jandals task

Name	Description of the algorithm
Algorithm 1	Share the word with someone who has three friends.
Algorithm 2	Share the word with someone who has three friends, and one of those three friends must have two other friends.
Algorithm 3	Share the word with someone who has three friends, and each of those three friends must have one other friend.
Algorithm 4	Share the word with someone who has three friends, and two of those three friends must have two other friends.

This group employed a patching mechanism (Moala, Yoon, & Kontorovich, 2018) when testing and refining their algorithms, changing only what needs changing (i.e., the faulty part of the algorithm observed at the testing stage) and keeping everything else the same. They also restricted their attention when refining their algorithms to localised considerations, specific cases in which the algorithm worked, while ignoring previous cases or other possible cases (Moala et al., 2018).

Implications for practice

In their present form, mathematical reflection sessions are not readily transferable to the classroom, as we have focused on studying them in carefully controlled instructional settings. Yet the format of reflecting teams can be modified and used in classrooms on smaller scales to encourage reflection and self-awareness regarding complex mathematical products and processes that students engage in. Mathematical comparison sessions are more immediately realisable in instructional settings, and are similar to follow-up activities (Radonich & Yoon, 2013) and formative assessment tasks (e.g., Swan & Burkhardt, 2014) that encourage students to critically examine other students’ solutions to a task they have also completed. Our project offers a new contribution in preceding these comparison sessions with reflection sessions which enables students to become more aware of their own mathematical product and processes before engaging in the critical examination of other students’ work. We hypothesise that the practice of enhancing student awareness of their own work before engaging critically with others’ may be more effective in developing mathematical sensitivity than critical examination alone.

Our findings about students’ piecemeal approach to creating and revising algorithms highlight the need for students to have more opportunities to create their own algorithms, rather than just applying ready-made ones. Alternative mathematical tasks like our risky mathematising tasks offer one instructional approach, and may be more feasible in discrete mathematics lessons, since the topic does not come with the same instructional baggage as more established topics like calculus. As job opportunities and everyday life become more dependent on digital technologies, mathematics curricula in schools and universities will need to place more emphasis on discrete mathematics to support the kinds of computational and algorithmic thinking needed for digital technologies.

We chose to frame the larger issue of the lack of alternative mathematical tasks in classroom practice as one of communication. We acknowledge that, in doing so, we have not addressed the many other barriers to implementation that teachers and researchers have battled for years, such as time constraints, institutional expectations, teacher knowledge and beliefs, and curriculum and assessment requirements. Yet we regard communication, particularly the kind that raises awareness for all involved, as a necessary means for making progress in these issues, and offer our project as a small step towards this. Clearly there is much more to be done.

Footnote

1. This approach uses network diagrams to describe the changing structures that students create and manipulate over time. SPOT stands for “Structures Perceived over Time”. ↑

References

Andersen, T. (1987). The reflecting team: Dialogue and meta-dialogue in clinical work. Family Process, 26(4), 415–428.

Barton, B., Davies, B., Moala, J., & Yoon, C. (2017). “How to” Guide #6: Generate conceptual readiness. Wellington: Ako Aotearoa—The National Centre for Tertiary Teaching Excellence.

Biesta, G. J. (2015). The beautiful risk of education. New York, NY: Routledge.

Clandinin, D. J., & Connelly, F. M. (2000). Narrative inquiry: Experience and story in qualitative research. San Francisco, CA: Jossey-Bass.

Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13.

DeBellis, V. A., & Goldin, G. A. (2006). Affect and meta-affect in mathematical problem solving: A representational perspective. Educational Studies in Mathematics, 63(2), 131–147.

Eisenberg, T., & Dreyfus, T. (1991). On the reluctance to visualize in mathematics. In W. Zimmermann, & S. Cunningham S. (Eds.), Visualization in teaching and learning mathematics (pp. 25–37). Washington, DC: Mathematical Association of America.

Fraivillig, J. L., Murphy, L. A., & Fuson, K. (1999). Advancing children’s mathematical thinking in everyday mathematics classrooms. Journal for Research in Mathematics Education, 30, 148–170.

Freudenthal, H. (1968). Why teach mathematics to be useful? Educational Studies in Mathematics, 1, 3–8.

Hart, E. W., & Sandefur, J. (Eds.). (2017). Teaching and learning discrete mathematics worldwide: Curriculum and research. Cham, Switzerland: Springer.

Ivey, A. E., Ivey, M. B., & Zalaquett, C. P. (2014). Intentional interviewing and counseling: Facilitating client development in a multicultural society. Boston, MA: Cengage Learning.

Joseph, D. (2004). The practice of design-based research: Uncovering the interplay between design, research, and the real-world context. Educational Psychologist, 39(4), 235–242.

Kontorovich, I., Koichu, B., Leikin, R., & Berman, A. (2012). An exploratory framework for handling the complexity of mathematical problem posing in small groups. The Journal of Mathematical Behavior, 31(1), 149–161.

Lesh, R., & Doerr, H. M. (2003). Beyond constructivism: Models and modeling perspectives on mathematics problem solving learning, and teaching. Mahwah, NJ: Lawrence Erlbaum Associates.

Lockhart, P. (2009). A mathematician’s lament: How school cheats us out of our most fascinating and imaginative art form. New York, NY: Bellevue Literary Press.

Maaß, K. (2006). What are modelling competencies? ZDM, 38(2), 113–142.

Maciejewski, W., & Star, J. R. (2016). Developing flexible procedural knowledge in undergraduate calculus. Research in Mathematics Education, 18(3), 299–316.

Mason, J. (2003). On the structure of attention in the learning of mathematics. Australian Mathematics Teacher, 59(4), 17–25.

Mason, J., Burton, L., & Stacey, K. (1982). Thinking mathematically. London, UK: Addison-Wesley.

McKenney, S., & Reeves, T. C. (2012). Conducting educational design research. New York, NY: Routledge.

Moala, J. G., Yoon, C., & Kontorovich, I. (2018). The emergence of a prototype of a contextualized algorithm in a graph theory task. To appear in the Proceedings of the 21st Conference on Research in Undergraduate Mathematics Education, San Diego, CA.

Morrow, L. J., & Kenney, M. J. (1998). The teaching and learning of algorithms in school mathematics. 1998 yearbook. Reston, VA: National Council of Teachers of Mathematics.

Niss, M., Blum, W., & Galbraith, P. L. (2007). Introduction. In W. Blum, P. Galbraith, H. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: The 14th ICMI study (pp. 3–32). New York, NY: Springer

OED Online. (2018). www.oed.com/view/Entry/137578. Accessed 4 June 2018. Oxford University Press.

Paré, D. (2016). Creating a space for acknowledgment and generativity in reflective group supervision. Family Process, 55(2), 270–286.

Pfannkuch, M., & Budgett, S. (2016). Markov processes: Exploring the use of dynamic visualizations to enhance student understanding. Journal of Statistics Education, 24(2), 63–73.

Radonich, P., & Yoon, C. (2013). Using student solutions to design follow-up tasks to model-eliciting activities. In A. Watson et al., (Eds.), Proceedings of ICMI Study 22: Task design in mathematics education, (pp. 259-–268). Oxford, UK: Springer.

Rittle-Johnson, B., & Star, J. R. (2011). The power of comparison in learning and instruction: Learning outcomes supported by different types of comparisons. In J. P. Mestre & B. H. Ross (Eds.), Cognition in education (Vol. 55, pp. 199–226). Oxford, UK: Academic.

Roth, W. M., & Maheux, J. F. (2015). The visible and the invisible: Mathematics as revelation. Educational Studies in Mathematics, 88(2), 221–238.

Schoenfeld, A. H. (1985). Mathematical problem solving. New York, NY: Academic Press.

Shapiro, S. (1997). Philosophy of mathematics: Structure and ontology. New York, NY: Oxford University Press.

Sinclair, N. (2004). The roles of the aesthetic in mathematical inquiry. Mathematical Thinking and Learning, 6(3), 261–284.

Stigler, J. W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York, NY: Free Press.

Swan, M., & Burkhardt, H. (2014). Lesson design for formative assessment. Educational Designer, 2(7), 1–24

Thomas, M. O. J. (2014). Algorithms. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 36–38). Netherlands: Springer.

Treffers, A. (1987). Mathematics education library. Three dimensions: A model of goal and theory description in mathematics instruction— the Wiskobas Project. Dordrecht, Netherlands: D Reidel Publishing Co.

White, M. (2000). Reflecting-team work as definitional ceremony revisited. In M. White (Ed.), Reflections on narrative practice: Essays and interviews (pp. 59–85). Adelaide: Dulwich Centre Publications.

Yoon, C. (2015). Mapping mathematical leaps of insight. In S. J. Cho (Ed.), Selected regular lectures from the 12th international congress on mathematical education (pp. 915–932). Switzerland: Springer.

Yoon, C., Chin, S. L., Moala, J. G., & Choy, B. H. (2018). Entering into dialogue about the mathematical value of contextual mathematising tasks. Mathematics Education Research Journal, 30(1), 21–37.

Yoon, C., Moala, J. G., & Chin, S. (2016). The jandals problem. Unpublished manuscript.

Yoon, C., Patel, A., Radonich, P., & Sullivan, N. (2011). LEMMA: Learning environments with mathematical modelling activities. Wellington: NZCER Press.

Author team

Caroline Yoon and John Griffith Moala The University of Auckland c.yoon@auckland.ac.nz

Acknowledgements

The authors wish to thank the teacher partners and the student participants for their valuable contributions to this project. We gratefully acknowledge the support of the Teaching and Learning Research Initiative. Finally, we acknowledge and thank the other members of the research team: Sze Looi Chin, Jean-François Maheux, Igor’ Kontorovich, Amy Linford, and Sarah Penwarden