Investigating the Impact of Non-Routine Problem Solving on Creativity, Engagement and Intuition of STEM Tertiary Students

1. Introduction

In 2012 the New Zealand Government identified as a priority the need to address the undersupply of students studying STEM subjects for delivering its Business Growth Agenda.^[1] Low engagement and retention rates in STEM subjects contribute to the shortage of STEM graduates, producing a negative impact on the New Zealand economy.

A significant number of STEM tertiary students drop out during the first year, not because the courses are too difficult but, anecdotally, because they are too dry and boring. There are specific terms to describe this, such as academic disengagement and disinterest (Blondal & Adalbjarnardottir, 2012).

In addition to specific subject-based knowledge, many high-tech companies require good generic problemsolving and thinking skills from their employees. To select the best, companies often use puzzles at their job interviews. Management at high-tech companies believe that the ability to solve puzzles relates to the creative thinking needed for solving real-life problems in innovative ways. A classic example is Microsoft, where the goal of interviews is to assess general problem-solving ability rather than specific knowledge. Microsoft see parallels between the reasoning used to solve puzzles and the thought processes involved in solving real, innovative problems (Poundstone, 2000).

The issue of hiring creative problem-solvers is also very important and timely in the New Zealand context. At the launch of Auckland University of Technology’s (AUT’s) STEM Tertiary Education Centre (STEM-TEC) in 2014, Hon Steven Joyce commented that many New Zealand innovative high-tech companies could not find suitable employees in New Zealand. They had to go through a long and expensive recruitment process hiring staff from overseas instead of employing recent graduates from New Zealand. Although many local applicants with suitable degrees could do routine jobs very well, companies needed candidates with highly innovative and creative thinking skills. This is consistent with the Vision Mātauranga (New Zealand Ministry of Research, Science and Technology, 2007) that encourages a spirit of creativity and innovation, in particular for research and development as “the place where creative thinkers focus on key issues, problems and creative possibilities” (p. 22).

Positive feedback from students, lecturers, and researchers on the regular use of pedagogical strategies employing non-routine problems and puzzles has been reported from several studies (see, for example, Falkner et al., 2012; Thomas et al., 2013; Klymchuk, 2017). In particular, the authors of the above studies noted that interesting non-routine problems, including puzzles, can engage students’ emotions, creativity, and curiosity and also enhance their conceptual understanding, critical thinking skills, problem-solving strategies, and lateral “outside the box” thinking.

There are clear links between skills developed by solving non-routine problems and puzzles and professional skills required in the workplace. Parhami (2008) argues that puzzling problems are plentiful in all research arenas regardless of discipline and, since many engineering problems are puzzle-like, engineering students should be exposed to them.

In line with the above, the genesis of this research was a pilot project funded by Ako Aotearoa in 2016, entitled “Enhancing generic thinking skills of tertiary STEM students through puzzle-based learning”. In that study, the introduction of puzzles in university STEM-subject teaching was trialled and found to have the potential to improve outcomes for students (Klymchuk et al., 2017).

Hence, this TLRI-funded project implemented and evaluated a pedagogical intervention aimed at enhancing learner engagement in STEM courses and increasing learners’ creativity more generally. It involved a partnership between a number of disciplines and institutions, providing a variety of expertise and experience. Specifically, the core project team of 10 comprised mathematicians, physicists, computer scientists, and educational psychologists (scholars and practitioners) from AUT, the University of Auckland, Manukau Institute of

Technology, and Whitireia New Zealand. Our partnership also included a group of prominent strategic advisors (see the acknowledgements section at the end of this report).

2. Research aim

The primary aim of our project was the evaluation of a strategic and innovative pedagogical intervention based on Puzzle-Based Learning (PzBL) in undergraduate STEM courses.

To fulfil this aim, the project sought to answer three important research questions:

• Does the integration of non-routine problem-solving in lectures affect participants’ engagement in lectures, and/or their ability to inhibit intuitive thinking and exhibit creative thinking?
• Are any observed effects moderated by individual differences such as demographic characteristics or prior ability?
• How do students react to the integration of non-routine problem-solving in their lectures?

3. Theoretical frameworks

The research considered the potential effects of non-routine problems on tertiary students’ engagement with STEM subjects in lectures, and students’ motivation and ability to exhibit creative thinking and to inhibit intuitive thinking. In this study a non-routine problem means one for which the students do not have a ready-made method of solution they can apply, but the content is still within the scope of their knowledge base (Selden et al., 2000). These problems include puzzles that cannot be solved by rote, are presented in an entertaining way, look deceptively simple but have unexpected answers and counter-intuitive solutions, and hence are invaluable to promote reasoning that involves both logical and creative thinking (Thomas et al., 2013). They could also include paradoxes, which have a surprising, unexpected, counter-intuitive statement that looks invalid but in fact is true, and sophisms, which involve intentionally invalid reasoning that looks formally correct but contains a subtle mistake or flaw. Some illustrative examples of such non-routine problems are:

• The Race. In a 100-metre race, athletes A, B, and C all run at a uniform pace. If A beats B by 10 metres and B beats C by 10 metres, by how much does A beat C? (Many students answer 20 metres, but the correct answer is 19 metres.)
• The Average Speed. You drive a car from A to B at a constant speed of 40 km/h. What should your constant speed be for the return trip from B to A if you want to obtain the average speed of 80 km/h for the whole trip? (Many students answer 120 km/h, but the correct answer is “infinite speed” or “impossible”.)
• Crossing the Bridge. Four people—John, Paul, George, and Ringo—are at one side of a gorge connected to the other by a rope bridge that can only carry two people at a time. It is a night-time, so whoever is crossing must use a torch. The group has a single torch, and the gorge is too wide for them to be able to throw it from one side to the other, so the torch must be walked back and forth over the bridge as the people cross. John can cross the bridge in 1 minute, Paul in 2, George in 5, and Ringo in 10. If two people cross together, they walk at the speed of the slowest of the two. How do the group cross the bridge in the quickest possible time? What is the quickest time? (Many students answer 19 minutes, but the correct answer is 17 minutes.)

The pedagogical theory informing the project was the Puzzle-Based Learning (PzBL) approach developed by Michalewicz and Michalewicz (2008) that has been adopted in many educational settings worldwide. Below we present the theoretical considerations related to the three major aspects of the project: engagement, intuition, and creativity.

3.1 Engagement

The first area of focus in this research was the potential effects of non-routine problem-solving on student engagement. The relationship between engagement and student participation, learning, and performance has been a growing area of investigation in mathematics and other STEM disciplines (Fredricks, 2011; Fredricks et al., 2016; Watt & Goos, 2017). Although engagement has been seen as related to motivation, engagement and motivation are generally viewed as distinct constructs (Fredricks et al., 2016). Definitions of engagement usually include active involvement with the content of a learning activity (Helme & Clarke, 2001), and often categorise it into behavioural, cognitive, and emotional dimensions, which align with doing, thinking, and feeling.

Emotional engagement was not directly considered in this research. Behavioural engagement refers to participation inside and outside the lecture theatre, including student conduct, persistence, participation, group work, concentration, and commitment to the course. Its theoretical foundation stems from expectancy-value theory (Eccles et al., 1983), which postulates that personal beliefs about one’s competence in learning can determine specific behaviour. For instance, learners may display cooperative behaviour in class if they perceive themselves to be competent enough to perform challenging activities. Cognitive engagement relates to the thinking that students do while engaged in academic learning tasks activity (Helme & Clarke, 2001). It involves students’ personal investment in learning, their self-regulatory strategies (Fredricks, 2011), flexibility in problem solving, preference for hard work, and positive persistence in the face of failure (Connell & Wellborn, 1991), as well as a willingness to exert the effort necessary to comprehend complex ideas (Ahlfeldt et al., 2005). In general, cognitive engagement is considered to have an effect on learning outcomes. The positive relationship of engagement to learning raises the importance of creating engaging learning experiences for students.

The tasks that teachers employ can impact engagement if the tasks create opportunities for learners to engage in activity that is interesting, meaningful, and challenging (Ryan, 2000), leading to improved engagement (Helme & Clarke, 2001). Tasks that are both interesting and emphasise higher-order skills and real-world applications have been shown to lead to better engagement (Fredricks, 2011). Other research (Jaworski et al., 2012) has proposed that inquiry-based non-routine questions, or tasks where the approach is not immediately obvious, such as those employed in our study, will encourage deeper student engagement.

To examine the nature of student engagement in solving non-routine problems, we used an instrument based on expectancy-value theory (Eccles et al., 1983). This posits that academic engagement is influenced by two categories of beliefs: learner expectations of success; and learner perception of the value of tasks. It has been shown that learners’ subjective task-value beliefs are strong predictors of engagement (e.g., Wigfield & Eccles, 2000).

3.2 Intuition

The second focus area in this research was to investigate the potential effects of non-routine problemsolving on students’ ability to inhibit intuition. Most mathematicians consider intuition as an important aspect of their work, with Burton (1999) reporting, “Intuition, insight or instinct was seen by most of the seventy mathematicians whom I interviewed as a necessary component for developing knowing” (p. 31). There is a complex relationship between intuition (which may be holistic or integrative) and logic/rigour in mathematics (which may be detailed or analytic). Both are important and complement each other, with Fischbein, who introduced intuition as a research domain in mathematics education, pointing out “the intuitive structures are essential components of every form of active understanding and of productive thinking” (Fischbein, 1982, p. 10). However, some researchers have warned that intuition can mislead and create misconceptions, and therefore sometimes should be inhibited (Attridge & Inglis, 2015; Thomas, 2015; Trémolière & Neys, 2014). Hence, it is sometimes important to be able to inhibit intuition when solving problems. In this case, inhibition refers to “the executive function in charge of stopping or overriding a mental process” (MacLeod, 2007, p. 3) or the act of suppressing distracting information and unwanted responses (Gilmore et al., 2015).

Some intervention studies have been conducted (e.g., Attridge & Inglis, 2015; Babai et al., 2015) in an attempt to improve students’ ability to overcome intuitive interference, such as introducing a warning to overcome automatic processing of certain variables (Babai et al., 2015). Attridge and Inglis (2015) found that prefacing tasks where intuition might mislead students with a task that is slow and effortful, thus requiring the use of working memory, was beneficial to inhibiting misleading intuition. Similarly, Babai et al. (2015) found that an explicit warning during task activity activated inhibitory control mechanisms and helped students overcome the interference. In this research, we studied the effect of an intervention employing non-routine problem-solving on inhibiting intuition. In order to examine effects on inhibition of intuition, we used an extended and slightly modified Cognitive Reflection Test (CRT) (Frederick, 2005) and a convergence task based on selected counterintuitive puzzles from Klymchuk (2001) (see Appendix).

3.3 Creativity

The third primary focus of the project was on whether exposure to non-routine problem-solving could influence students’ creativity. Although it has proven relatively difficult to define creativity precisely as there are more than 100 definitions of creativity in literature, a number of intellectual qualities that may contribute to it have been considered. Among these is the divergent-production ability that is related to idea generation and elaboration abilities. Another source of creative thinking is a transformation ability, which pertains to one’s ability to connect old and new knowledge and hence create new ideas. One crucial characteristic of this ability is a readiness to be flexible, where flexibility leads to reorganisation and reinterpretation (Guilford, 1967).

Students who have developed flexibility or versatility (Thomas, 2008) in their thinking tend to be able to go beyond routine competencies, be more innovative and creative, understand why procedures work, and modify or invent new procedures (Hatano & Oura, 2003). These creative aspects of versatile thinking may arise from an ability to translate within and between representations, to interact conceptually with representations, to switch between perceptions of a mathematical entity as a process or an object, and to exploit the power of visual schemas by linking them to relevant analytical ones (Thomas, 2004).

Creativity is a process that is often required in the solving of non-routine problems, since there is no available standard approach. It has been suggested (Wallas, 1926) that a creative approach to problem solving involves: (1) preparation (where the problem is “investigated in all directions”); (2) incubation (unconscious processing of information, cognitive processing); (3) illumination (a sudden insight or discovery of a solution); and (4) verification (deliberate testing and evaluating of the solution or idea). It is worth noting that each of these aspects of the creative problem-solving process requires a high level of student engagement. Students may go through various stages of this process of creative thinking in a recursive manner, since the most appropriate solutions will require further insightful thinking and verification. Creativity in our project was understood to be what Leikin (2009; see also Leikin & Pitta-Pantazi, 2013) calls “relative creativity” and Sriraman and Haavold (2016) refer to as “everyday creativity” (compared with “extraordinary creativity” or exceptional knowledge that changes perceptions of the world). To measure creativity, we used the highly influential theory of creativity developed by Guilford (1959, 1967), who considered creative thinking as divergent thinking based on fluency, flexibility, originality, and elaboration. When solving problems, fluency is identified as the ability to generate a great number of solutions; flexibility the ability to suggest a variety of approaches; originality the ability to propose unusual approaches; and elaboration the ability to organise the details of an idea and implement it.

In summary, this project utilised a PzBL approach based on non-routine problem-solving in lectures to analyse its influence on the focus areas of student engagement, intuition, and creativity. The relationship between engagement and student learning is well established, and creativity, which has links to engagement, is crucial to problem-solving of all kinds. Further, while intuition is important in solving problems, it can sometimes create misconceptions and then needs to be inhibited. These focus areas led to the following design for the study.

4. Research design and methodology

A design-based methodology, utilising both quantitative and qualitative data, was employed in the current research. This approach has gained prominence as an effective methodology in mathematics education research (e.g., Cobb et al., 2003; Prediger et al., 2015). The aim of design research is to “yield useful knowledge … that is sensitive to context and yet general enough to use in new situations” (Bakker, 2018, p. 47). Such knowledge is often summarised in the form of design principles, which are updated in the iterative process of micro- and macro-cycles. The first macro-cycle of this design research project took place in 2016 in the pilot project funded by Ako Aotearoa. The second macro-cycle, the current project, began in 2018.

4.1 Participants and procedures

In the current project, there were 683 eligible undergraduate Year 1 and Year 2 students studying 12 STEM courses in astronomy, computing, engineering, and mathematics at four tertiary institutions in New Zealand: AUT (152 students), the University of Auckland (440 students), Manukau Institute of Technology (25 students), and Whitireia New Zealand (66 students). During the first week of the first semester 2018, all students were invited to participate in the study via a verbal announcement in a lecture and an online invitation. Out of the 683 students, 100 students (approximately 15% of those invited) volunteered but only 64 students completed both pre-test and post-test questionnaires (a 9% response rate). Thus, the final sample included 36 males (56%), 27 females (42%), and one gender diverse student (2%); 58 were younger than 25 years old (91%) and the remaining six participants were over 25 years old (9%). In addition to this sample of participants who completed both questionnaires, there were two smaller samples of participants: (1) 12 student participants who volunteered for a one-hour task-based interview (these are numbered S1-S12 in the analysis), and (2) nine lecturers involved in the intervention (including five from the project team) who completed the lecturer questionnaire by email. Participating students were rewarded with gift vouchers for their time. The project was approved by the University of Auckland Human Participants Ethics Committee on 5 June 2018 (ref. number 021387) with subsequent approval by the other three tertiary institutions.

Students were exposed to the regular use of puzzles in lectures as a co-curricular activity over a 12-week semester. Their lecturers were invited to the study and were given instructions and a selection of puzzles. They agreed to incorporate the puzzles activities in their lectures. Typically, three or four puzzles were presented to the students in one or two lectures every week. Students had a choice to solve puzzles either individually or in groups. Then a student or a lecturer showed the solution with a short explanation/discussion. The duration of this activity was 5–7 minutes a week. Hence, while the intervention involved solving and discussing a total of up to 40 puzzles over a 12-week semester, the intervention was short, comprising less than 5% of weekly lecture time. None of the other components of the course delivery (tutorials, assignments, tests, and examinations) were involved, as the intervention was designed by the project team to be easily incorporated into existing courses by slightly tuning the pedagogical practice in lectures.

4.2 Instruments

Several different types of instruments were used to gather data to address the research questions. All of them—the student pre-test (in week 1) and post-test (in week 12) questionnaires, content validation survey questions for the pre- and post-test questionnaires, focus group interview indicative questions, the lecturer questionnaire, and class observation protocol—are attached in the appendix to this report.

The student pre- and post-questionnaires were designed to measure several psychological constructs or capacities (e.g., engagement, response inhibition, creativity) using questions from the following sources:

1. engagement—validated questionnaire of Ahlfeldt et al. (2005), which was developed based on the USA’s National Survey of Student Engagement (NSSE) (2000). The questionnaire comprised 17 self-assessment items and assessed three latent factors related to solving non-routine problems: participants’ self-efficacy (a = .76 at T1 and .84 at T2), intrinsic interest (a = .89 at T1 and .88 at T2), and utility value (a = .72 at T1 and .75 at T2)
2. inhibition of intuition—an extended and slightly modified Cognitive Reflection Test (CRT) that included the original CRT (Frederick, 2005) as well as two questions inspired by Babai et al. (2015)
3. convergent thinking—the Convergence Task based on selected counter-intuitive puzzles from Klymchuk (2001); and
4. divergent thinking/creativity—an Alternative Uses Test from the well-established Torrance Test of creativity (Torrance, 1963) based on Guilford’s model of creativity (1959). Specifically, students were asked to list as many uses as possible for either a brick (Form A) or a shoe (Form B) in a short time.

Given the importance of student engagement in this project, the foregoing self-reporting was triangulated by lecturer feedback and lecture observations. The nine lecturers involved in the intervention provided feedback on the engagement of their students by email response to a questionnaire. In addition, observers were present in five of the lectures in two different tertiary institutions and recorded the time spent in class on nonroutine problems, the number of problems introduced in each lecture, the quality of delivery, and the active engagement of the students. This active engagement was measured in two ways. One method was a five-point scale, indicating the observers’ perception of engagement (from low to high); the other was a more in-depth observation, sampling and recording student off-task behaviour. In each lecture, the observer visually scanned a sample of approximately 30 students, noting in a chart any students demonstrating off-task behaviour. This observation was repeated every five minutes, with particular attention given to the timing of the delivery of the non-routine problems.

The SPSS 23 program was used for all statistical analyses, including Chi-square tests, t-tests, Friedman test, parametric test, and Repeated Measures ANOVAs. The majority of the 64 students answered all or most of the questions but occasionally there were missing data.

5. Results

5.1 Student engagement

As detailed in the preceding section, student engagement was assessed in several ways. Specifically, in this section we present results from: (1) in-lecture (real-time) observations of students’ behavioural engagement; (2) students’ self-reported responses on pre- and post-questionnaires concerning their academic engagement; and (3) lecturer reports of student engagement.

5.1.1 Behavioural engagement: Results from lecture observations

Based on five independent lecture observations (before, during, and after the intervention), students’ behavioural engagement was found to be significantly greater during the time period the intervention was used. As detailed in Figure 1, the same U-shaped pattern of off-task behaviour (decreasing from Before to During, then increasing from During to After) was observed across all five lectures.

FIGURE 1. Mean number of students per observation with off-task behaviour.

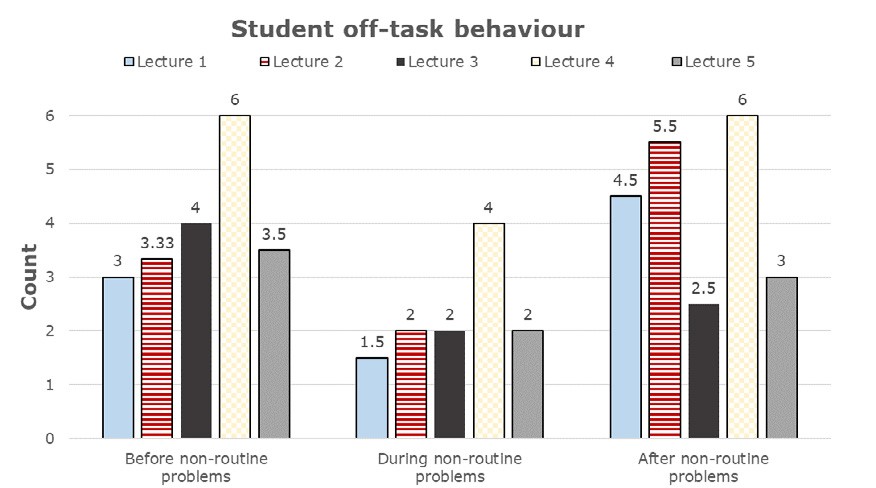
Results from a Friedman test confirmed that there was a statistically significant difference in the off-task behaviour across the three time points during the lectures, χ²(2) = 7.90, p =.019. Specifically, more instances of off-task behaviour were observed before the intervention (median = 3.5) than during (median = 2); a median difference decrease of 1.5 followed by a median difference increase of 2.5 after the intervention (median = 4.5) (p=.053 for both pairwise comparisons for Before–During and During–After, adjusted by Bonferroni corrections for multiple tests).

The rise and fall of student engagement and the consistency of the data across all observed lectures in five different courses shows a noteworthy pattern. In short, these data provide strong evidence that students found the non-routine problems engaging.

5.1.2 Academic engagement: Results from student questionnaires

The almost equal values of the three factors recorded at different times of the semester demonstrated trait-like stability of the corresponding latent constructs (Figure 2).

FIGURE 2. Mean factor scores for students’ self-reported self-efficacy, intrinsic interest, and utility value at the beginning (Time 1) and end (Time 2) the semester.

NOTE. -2=strongly disagree, -1=disagree, 0=neutral, 1=agree, 2=strongly agree

While the measures of each factor vary slightly, all mean values are in the positive half-plane. This demonstrates that students mostly agreed that they perceived themselves to be capable at solving non-routine problems, indicating positive levels of self-efficacy in solving them. They also agreed that knowing how to solve nonroutine problems was useful for their learning and could enhance their creative and innovative thinking abilities. Further, they enjoyed solving them, presumably indicating overall positive emotional disposition. However, results from repeated measures ANOVA indicated that there were no main effects for time on any of the three variables. This suggests that the intervention did not, on average, affect participants’ self-efficacy, intrinsic interest, and utility value related to solving non-routine problems.

5.1.3 Academic engagement: Prior achievement as a moderator of change over time

Our research agenda had a particular focus on students considered to be at high risk of withdrawal—the group of students usually associated with low academic engagement. In the context of our study, this group comprised those with low grades in the prerequisite courses. To compare the beliefs of students at the beginning and end of the semester, and whether these would differ based on student grade, we ran three two-way mixed ANOVA tests to determine the interaction effect of time and students’ prerequisite grades on these measures. The independent ordinal variable was the prerequisite course-specific grades the students reported, grouped in bands: A grade (N=21), B grade (N=20), and C grade (N=12) bands. Descriptive statistics are summarised in Table 1.

TABLE 1. Descriptive statistics of the latent constructs per grade band.

Latent constructs	Grades	Mean	Std. Deviation
Self-Efficacy at Time 1	C-grade band	.4375	.65821
	B-grade band	.3500	.85224
	A-grade band	.5476	.49129
Self-Efficacy at Time 2	C-grade band	.5625	.73951
	B-grade band	.4250	.95318
	A-grade band	.4405	.48673
Intrinsic Interest at Time 1	C-grade band	1.1875	.55519
	B-grade band	.8000	.89443
	A-grade band	1.2262	.56405
Intrinsic Interest at Time 2	C-grade band	1.3333	.59671
	B-grade band	.8500	.88630
	A-grade band	1.0952	.63971
Utility Value at Time 1	C-grade band	1.2083	.74493
	B-grade band	.9000	.66590
	A-grade band	1.2381	.48397
Utility Value at Time 2	C-grade band	1.2292	.39107
	B-grade band	1.0375	.74018
	A-grade band	1.2976	.52808

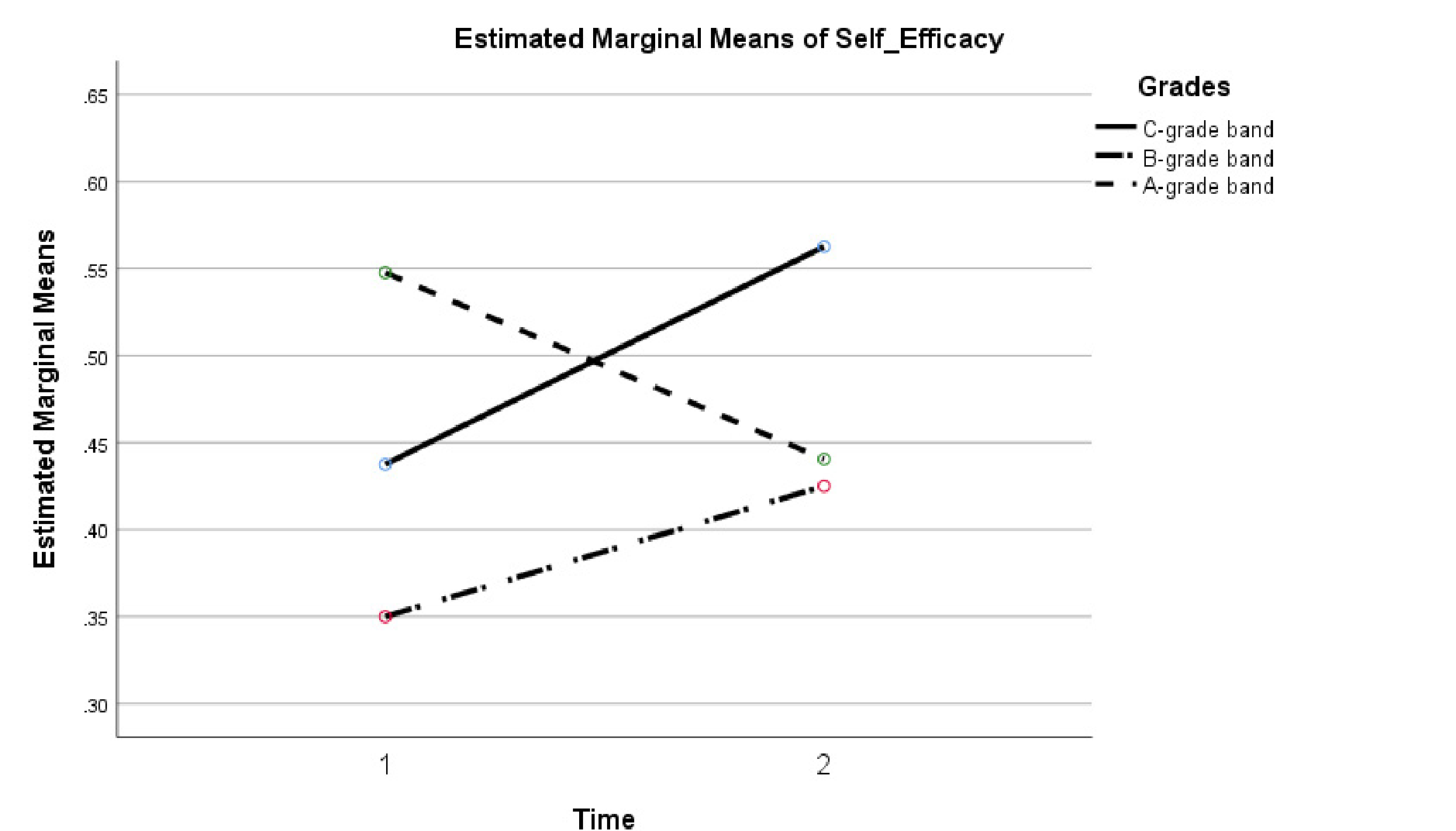
Self-efficacy: Although neither the main effect of time (F(1, 50) = .20, p = .660) nor the interaction effect (F(2, 50) = 1.09, p = .343) were statistically significant, the effect size (partial η²= .042) suggests a small size effect for the interaction. Specifically, as depicted in Figure 3, while participants from the A-grade band reported a decrease in self-efficacy for solving non-routine problems (D M = –.11), participants from the B-grade band and C-grade band reported an increase in their self-efficacy to do so (D M’s = .08 and .13, respectively). These small changes over time are unlikely to represent meaningful shifts, given the small eta-squared and non-significant main and interaction effects.

FIGURE 3. Self-efficacy for non-routine problem-solving at Time 1 and Time 2 by grade band.

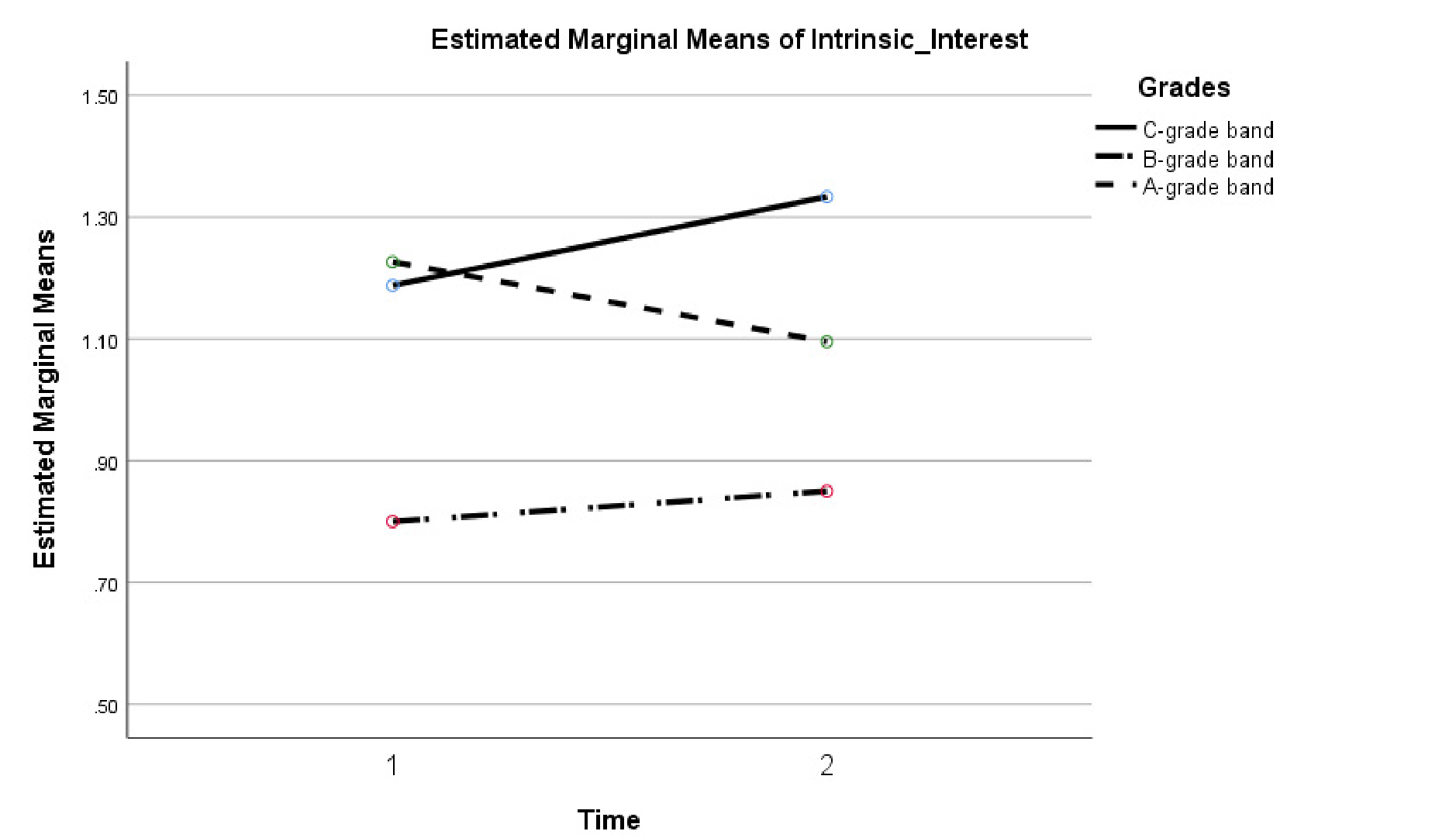
Intrinsic interest: Again, neither the main effect of time (F(1, 50) = .07, p = .788) nor the interaction effect (F(2, 50) = 1.04, p = .360) were statistically significant, but the effect size (partial η²= .040) suggests a small size effect for the interaction. Specifically, as depicted in Figure 4, while participants from the A-grade band reported a decrease in intrinsic interest (DM = -.13), participants from the B-grade band and C-grade band reported an increase in intrinsic interest (DM’s = .05 and .15, respectively). As with the results for self-efficacy, these small changes over time are difficult to attribute to the intervention and are just as likely to be a statistical artefact known as “regression to the mean” (whereby those who score above/below average at Time 1 score closer to the mean or average at Time 2).

FIGURE 4. Intrinsic interest in non-routine problem-solving at Time 1 and Time 2 by grade band.

Utility value: Neither the main effect of time (F(1, 50) = .761, p = .387) nor the interaction effect (F(2, 50) = 1.70, p = .844) were statistically significant, but the effect size (partial η²= .015) suggests a small size effect of time. In this case, participants’ perceptions of the utility value of non-routine problem-solving appear to have improved at the end of the semester in all grade bands (DM’s =.06, .14, and .02, for A-, B-, and C-grade bands, respectively).

The lack of statistically significant differences in measures of all three latent constructs illuminates an equalising aspect of non-routine problem-solving, meaning that student grade in a prerequisite course says very little about student self-efficacy in non-routine problem-solving, emotional disposition toward it, or its perceived value. Small size interaction effects observed in the measures of the first and second constructs capture nonsignificant group differences with respect to time. Notably, the largest increase in self-efficacy and intrinsic interest seems to have been reported by students from the low-achievement group (C-grade band).

5.1.4 Academic engagement: Results from student questionnaires

To examine student engagement from a different perspective, we assessed a more “global” measure of student engagement in the entire semester course using a well-known instrument of Ahlfeldt et al. (2005) (see Appendix). The metric indicator of student engagement was the course engagement score (ES)—a summative score of all 14 items. The range of ES scores was broad (24 to 55), with an overall mean of 34.85, indicating a moderate level of engagement when compared to the aggregated engagement scores reported in Ahlfeldt et al.’s (2005) study. However, it is notable that the ES score in the present study is higher than the matching category “Science and Mathematics” in the Ahlfeldt et al. (2005) study, where a range from 27 to 39 and overall mean of 33.57 were reported from seven courses.

An extra question was specifically included in the same questionnaire to gauge self-reported engagement with the intervention: “With respect to this course, about how often have you worked on solving puzzles and/or creative problems during class?” The aim was to identify differences between students with different prerequisite grades.

A one-way ANOVA was used to analyse the differences. Although the effect of prerequisite grades was not statistically significant (F(2, 52)=1.61, p= .610), the effect size (partial η²= .058) suggests a small size effect. Specifically, as depicted in Figure 5, participants who reported earning a C in the prerequisite course reported the highest level of engagement with non-routine problem-solving (M = 3.08, SD = .73), while participants in the B-grade band reported the lowest level of engagement (M = 2.45, SD = 1.07). There was no Bonferroni adjustment made. This finding was unexpected and may have nothing to do with the intervention.

FIGURE 5. Self-reported engagement in non-routine problem-solving during the course by grade band.

Notes: With respect to this course, about how often have you worked on solving puzzles and/or creative problems during class? (4=Very Often, 3=Often, 2=Occasionally, 1=Never)

ERROR BARS: +/- 2 SE

5.1.5 Academic engagement: Results from lecturer responses

Finally, analyses of data from nine lecturers supported the hypothesis that students experienced an increase in engagement as a result of the intervention. In responding to the first questions (“To what extent were students engaged with the puzzles? Was there any evidence of engagement?”), eight lecturers observed that most of their students were engaged with the puzzles to a large degree. In terms of the evidence they provided to support this, four lecturers reported that students “asked to do more puzzles”, asked for “additional sets of puzzles” or for “books containing the puzzles”, and also “expressed disappointment if I didn’t get to do a puzzle during a lecture”.

Two lecturers mentioned that students appeared to be more active or engaged during the puzzle activity: “[students] looked more active and liked to participate during the puzzle time”; and “the puzzles helped students feel more engaged and able to interact with/interrupt the lectures”.

Responding to the second question (“Did students’ engagement change over time?”), five lecturers reported an increase in student engagement over time: “with time the interest was growing and at the end of the semester students asked me in corridors when puzzles will be presented again”; “over the weeks there was more discussion in groups”; “yes, increased”; “more engagement over time”; and “the levels of discussion and engagement by students was increased”. One lecturer observed that the change in engagement depended on the level of student interest: “their engagement changes depending on the content (interesting or not) of the puzzle”. However, two lecturers were unable to make a judgment on whether engagement changed: “not really sure”; “I did not sense the level of engagement changed much”; and one lecturer did not answer this question.

5.2 Student intuitive and convergent thinking

As detailed in Table 2, results from paired-sample t-tests indicated that participants’ intuitive thinking did not change significantly over time. Specifically, the mean CRT score for all participants at Time 2 was .77, a small increase of .02. There was some variation in mean change based on the sequencing of test forms participants received. For example, while participants who completed Form A of the CRT (the original version) at both Time 1 and 2 earned the highest overall mean scores (.87 at T1 and .81 at T2), they experienced the greatest decrease in mean score over time. Conversely, participants who completed Form B at T1 and Form A at T2 started with the lowest mean score at T1 (.65) but experienced the greatest increase over time (DM = .13). Although not statistically significant, the latter increase constitutes a small to medium size effect (Cohen’s d = 0.41). In short, it appears that Form A and B were not equivalent forms (the latter proving more difficult than the former), and that the notable increase demonstrated by those that completed Form B at T1 and Form A at T2 may likely be the result of between-form differences in item difficulty.

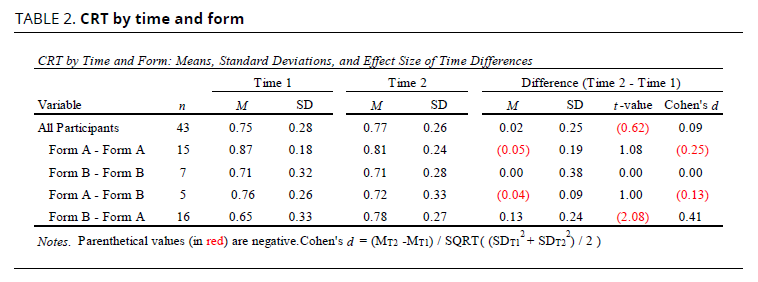
Similarly, results from paired-sample t-tests indicated that participants’ convergent thinking did not change significantly over time. Specifically, the mean score for all participants at T1 was .55 and at T2 was .53, a small decrease of .02. As seen in Table 3, there was some variation in mean change based on the sequencing of test forms participants received. This time it was participants who completed Form B both times who obtained the highest overall mean scores (.64 at T1 and .61 at T2) and experienced the greatest decrease in mean scores (0.04). Participants who completed Form A at T1 and Form B at T2 experienced the greatest increase over time (D M = .05). However, none of the differences was statistically significant (p > .05), and their magnitudes were very small (Cohen’s d < 0.30). In short, there were no notable changes in participants’ convergent thinking (problem-solving) ability over time, regardless of form sequencing.

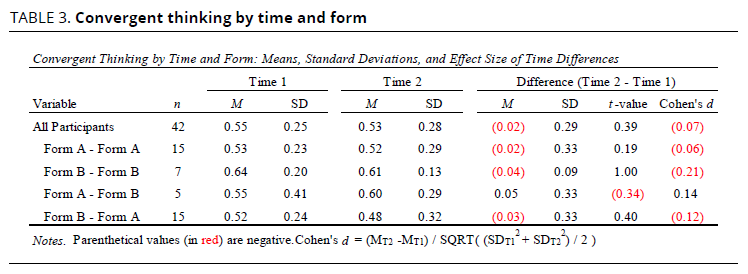
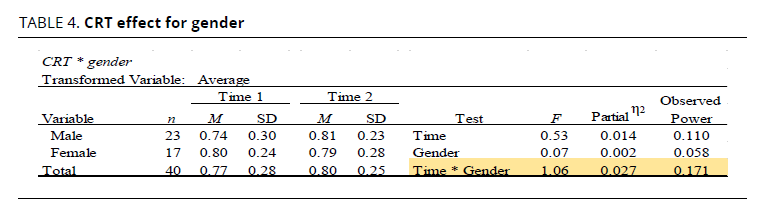
In summary, there were no significant main effects for time on either participants’ intuitive or convergent thinking. However, there was one interesting finding—a potential moderation effect for gender on the CRT. Specifically, whereas females did not demonstrate any notable change over time on the CRT (from .80 at T1 to .79 at T2), males demonstrated a small gain over time (from .74 at T1 to .81 at T2). While the observed difference was not statistically significant, the partial eta-squared value (0.27) signifies a small effect for the interaction (see Table 4) and suggests that the intervention may have been more effective for males than females.

5.2.1 Lecturer questionnaire

One question from the lecturer questionnaire on intuition was “Did you observe any change in the intuitive nature of the students’ initial attempts to answer the puzzles over the time?” Six out of nine lecturers reported that they observed a change. They commented:

When students noticed the problem solving often depended on the interpretation of the question, they started thinking around what was being asked. It opened the problem up for them in terms of the way they looked at the question.|

On the initial meetings where a puzzle was used, the students tried to solve the puzzle just by looking at it and thinking. The later meetings, they tried to use pictures made on paper. There was also more activity, when students discussed among them the possible solution at the latest meetings.

They tended to discuss more at the start and bounce ideas off each other which they weren’t doing at the start.

Students became more cautious with using their intuition as they saw it often mislead in puzzles.

Students were more willing to share their intuitions when solving the puzzles.

One lecturer did not observe any changes in intuition and two lecturers replied “Not sure”.

5.2.2 Focus group interviews: Intuitive thinking

The 12 students in the focus groups worked on solving given tasks as well as constructing their own. When asked to describe the kinds of thinking required to solve them, some referred to the need to control one’s thinking in some way, saying:

S7 When I’m doing a puzzle I will think about it at least twice … it may contain some traps.

S11 I often get caught out using intuition straightaway … [I] need to try using a more pragmatic approach, which would decrease the effect of my over-eagerness to find the solution.

S12 You … must not take your first intuitive-designed answer.

This idea of inhibiting intuition was a focus and the students agreed that it is important. They also expressed the need to get an overview of the problem as part of the creative process.

S3 Solving puzzles though one can have a strategy, don’t have formulaic approaches.

S10 Solving puzzles allows one to approach problems as a whole … instead of short term step by step.

S12 Creating something new: a perspective.

This desire for a strategic overview was linked by S11 to the need to inhibit intuitive thinking.

S11 Innovation helps to hold back intuition by developing a new strategy.

5.3 Student creativity

The impact of the PzBL intervention on students’ creativity was measured via a divergence task, some questions in the self-assessment section, feedback from the lecturer questionnaire, and problem-solving and problemposing tasks at the focus group interviews.

5.3.1 The divergence task

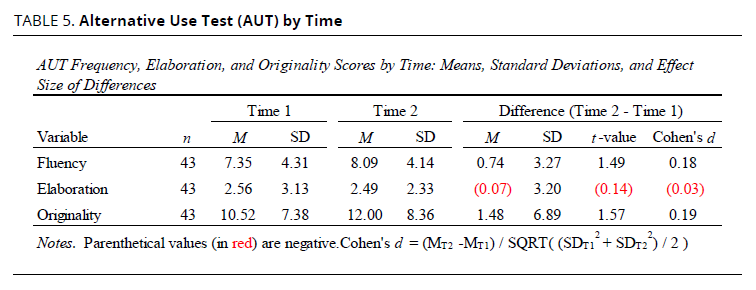
The divergence task was based on the Alternative Use Test. Students were asked to generate in a relatively short time as many alternative uses of a brick (form A) or a shoe (form B) as possible. Based on Guilford’s (1959) model of creativity, we measured the following traits of divergent thinking: fluency, elaboration, and originality. The originality score used was calculated based on the originality of the words or ideas generated in participant responses. As shown in Table 5, results from paired-sample t-tests indicated no significant differences in participants’ fluency, elaboration, or originality scores (all p’s > .05). That said, there were very small increases across time for both fluency and originality (Cohen’s d’s = 0.18 and 0.19, respectively).

5.3.2. Self-assessment section

In this section of the pre- and post-surveys, participants were asked to use a five-point Likert-type scale to indicate how strongly they agreed or disagreed with two statements related to creativity:

1. Solving puzzles can enhance your creativity.
2. Solving puzzles makes you a more innovative thinker.

The vast majority of students agreed with both statements at both times. Specifically, 87.8% of participants agreed or strongly agreed with the first statement at T1 and slightly more at T2 (90.2%). Similarly, while 82.9% of participants agreed or strongly agreed with the second statement at T1, slightly more did so at T2 (90.2%). The survey section also included the following open-ended question on creativity: “Do you think solving puzzles can enhance your creativity?” The vast majority of participants (86% on pre-survey and 84% on post-survey) agreed that solving puzzles could enhance their creativity. A common survey response to both questions 1 and 2 defined creativity in terms of the need to “think outside the box”: 12 times (pre-survey), and 15 times (postsurvey). About half the participants (47% pre-survey, 57% post-survey) thought they were less likely to focus on a single heuristic to get the correct answer: “It forces you to look outside the obvious first glance answer and think about other possibilities outside of the obvious.”

Other responses to this question (42% pre-survey, 45% post-survey) focused on notions of thinking differently. They stated that instead of applying a formula, they needed to access their prior knowledge and employ creative thinking in the problem-solving: “It teaches us to rely on our knowledge but not necessarily follow the formula of what we’ve been taught, but instead a good balance of prior knowledge and thinking `outside of the box’.” They agreed there was a need to think beyond commonly accepted ideas (“It helps you see that there are a lot of different ways to doing the same task or one standard way of doing a range of things”), and to interpret the questions in different ways (“It requires us to look at the question in different perspective and visualise the situation in our head”).

5.3.3. Lecturer questionnaire

The following question from the lecturer questionnaire addressed creativity: “Did you observe any change in creativity of the answers over the time you used puzzles?” Three lecturers answered “yes”, five “no”, and one “not sure”. Typical comments from the lecturers who answered “no” were “not enough time” for the intervention and/or the course was “too short”. Typical comments from the lecturers who answered “yes” were as follows: “Students were trying more diverse and sometimes crazy ideas and approaches”; “Students were more playful and less reserved when working with the puzzles.”

5.3.4. Focus group interviews: Creativity

Of the 12 students in the focus groups, 83% (10) agreed that innovative thinking was connected to solving non-routine problems. One focus group in particular seemed to do better than the others in producing a task involving some creativity. This group comprised S7, S8, and S9 and was given the following task:

Make up an interesting problem based on the information below. You may add extra information if required.

A car, A, is travelling due East at 30km/h. A second car, B, is travelling South West at 50km/h.

The response from this group was as follows:

The radius of a sphere is 400km. Cars A and B start at the same place and time and move in their designated directions and speeds. What is the sum of the distances that both have travelled before they meet again?

Setting aside the practical considerations of their problem, it is instructive to consider the group’s thought processes. They stated that they wanted to produce an “interesting” or non-standard problem and that doing this was related to being creative.

S7 Brainstorm to have some interesting idea. Should be something unusual.

S8 Creativity. The task is to create an interesting problem therefore creativity is important.

S9 To come up with something interesting and out of the box.

Moreover, all of them described this kind of creative thinking as “out of the box”. In addition to the quote from S9 above, they also said:

S7 Skills like thinking more carefully and thinking out of the box should be useful.

S8 My issue is I try to solve things like routine questions instead of thinking outside the box.

S9 The thinking is a lot more out of the box. You really have to stretch your brain more creatively.

It seems clear that the students recognised that solving non-routine problems is different from solving routine ones. It requires them to use different kinds of thinking, such as approaching the problems with a holistic strategy rather than linearly, thinking more creatively, and attempting to inhibit their intuitions.

5.4 The impact on employability

The impact of the PzBL intervention on students’ employability was measured via the self-assessment section and focus group interviews.

5.4.1 Self-assessment section

In this section of the pre- and post-surveys, participants were asked to use a five-point Likert-type scale to indicate their agreement or disagreement with the statement: “The knowledge and skills related to solving puzzles will be useful to me in the future.” The vast majority of students agreed with this at both times: 80.2% at T1 and over 10% more at T2 (90.3%).

Triangulating this was the open-ended question in the section on future benefits from solving puzzles: “Do you think solving puzzles can benefit you in the future?” The vast majority of participants (94% pre-survey, 92% postsurvey) agreed that solving puzzles could benefit them in the future. Some participants (32% pre-survey, 28% post-survey) specified particular ways they thought puzzles would be beneficial in their future careers, such as ”I hope to pursue a career in data science and science technologies”; “Absolutely, I am aiming to work as an Astronomer—possibly in the field of astrophysics, and math/physics are concerned with a multitude of realworld puzzles.” They also believed that employers expected employees to utilise problem-solving skills and that they would test these skills in job interviews: “I think employers look for people with good problem-solving skills”; “Employers look for people who have problem-solving skills. You are tested on this in interviews.”

In terms of personal growth and development, many participants (47% pre-survey, 59% post-survey) commented that they enjoyed solving puzzles, felt a sense of achievement, and thought it developed their creativity as well as their problem-solving skills: “I really enjoy them and get joy from them and a feeling of satisfaction and self-worth and pride when completing them”; “It gives me a feeling of achievement”; and “It enhances creative and problem-solving skills.” The utility value rates were higher than enjoyment rates.

Further, some participants (21% pre-survey, 11% post-survey) stated that puzzles could enhance problemsolving skills in their daily lives, at work (“It builds skills that are useful in the workplace/everyday life”), and when solving real-world problems (“You will learn problem-solving skills that you can apply in the real world”; “The world is evolving and there will be many puzzles to solve in this life, both as a society as a whole and personally”). Moreover, they expected their problem-solving skills to help with solving complex life problems (“Faced non-traditional problems in the real world”).

5.4.2 Focus group interviews: Employability

All 12 students agreed that the novel kinds of thinking gained from solving non-routine problems would be useful in other areas of life, citing as examples logistical issues, transport (such as flights), food packaging, climate change, house building, and other business environments.

5.5 Summary of results

We summarise here the main findings of the research that answer the research questions.

Engagement

• Students’ behavioural engagement was significantly greater during the intervention. The evidence showed that they found the problems more engaging than the lecture itself, with fewer instances of off-task behaviour observed.
• The group with C grades in prerequisite courses appeared to be the most engaged with non-routine problem-solving.

Self-efficacy

• Students mostly indicated positive levels of self-efficacy in solving non-routine problems. They saw themselves as capable of solving non-routine problems, and enjoyed doing so, indicating a positive emotional disposition.

Intuition

• Even though students saw the importance of inhibiting intuitive thinking, it did not change significantly over time.

Convergent thinking

• There were no significant changes in students’ convergent thinking (problem-solving) ability over time.

Creativity

• There were no significant changes in students’ creativity (originality, fluency, and elaboration traits of divergent thinking) over the intervention.

Group differences

• Grades in prerequisite courses did not significantly influence over time student self-efficacy in, emotional disposition toward, or perceived value of non-routine problem-solving. However, students with prior B- and C-band grades reported a small increase in self-efficacy and intrinsic interest.
• The results suggest that the intervention may have been more effective for males than females and this hypothesis could be investigated in future research.

Student perceptions about learning

• Students agreed that solving non-routine problems was useful for their learning and was able to enhance their creative and innovative thinking abilities. They talked about the need to “think outside the box” and think holistically rather than be focused on a single approach.
• Perceptions of the utility value of non-routine problem-solving improved at the end of the semester for all students.
• The students strongly agreed solving non-routine problems in their courses would be beneficial to their future learning, as well as their careers and other areas of life.

We anticipated a high level of student engagement during the PzBL intervention and this was realised. The feedback by the vast majority of the students also confirmed that they saw valuable benefits from the PzBL activities for their future employment. We also expected that the PzBL intervention would enhance students’ creativity and ability to inhibit their intuition. However, the increase in students’ creativity and ability to control their intuition before and after the intervention was not statistically significant. One possible reason for this could be the small timescale of the intervention with simply not enough time to exhibit such a change. Although the intervention was regular each week for 3 months, the total time was only about an hour. Having spent 10+ years in formal education where there was little or no attention paid to creativity in STEM subjects, students need more time to unlock their creativity. Many researchers point out that (primary) intuition is strongly present and very resistant to change (e.g., Fischbein, 1982; Thomas, 2015). Hence, these important aspects of enhancing creativity and the ability to inhibit intuition when necessary require further attention by researchers.

6. Implications and recommendations for practice

Increasing behavioural and cognitive engagement of students in tertiary institutions is extremely important, and behavioural and cognitive engagement are often used as indicators of improved learning (Kahu & Nelson, 2018; Watt & Goos, 2017). A primary outcome of this research is that an intervention employing non-routine problems significantly improved student engagement and induced very positive attitudes to the solution process. Hence, we would recommend that tertiary institutions seriously consider initiating a similar pedagogical strategy in their STEM subjects. While a few universities may already offer optional seminars or even compulsory courses based on PzBL for their first-year STEM students, this is far from the norm. University lecturers may think it is too difficult to adopt an approach to teaching that fosters student engagement, given their limited resources, large class sizes and the significant amount of time and effort required for class preparation. However, the results of this study suggest that with a relatively small effort, lecturers can improve student engagement by spending just a few minutes per lecture on non-routine problem-solving during STEM lectures—something that can be easily implemented, even for those who primarily teach using a traditional “transmission” style. Moreover, such an intervention is highly amenable to scaling up, with a relatively small development investment and easy transfer to other tertiary STEM courses since it requires minimal time allocation or lecturer preparation. The student voice in the process is also very important and regular student feedback—both formal and informal—will make the intervention more meaningful and successful.

In order to benefit fully, we recommend that lecturers consider working in small groups when implementing this practice. The research literature show the value of small communities of inquiry (Jaworski, 2006) in order to discuss ideas and provide support (Barton, et al., 2014) as they engage in critical inquiry into practice. This would also assist with planning, including preparation of the relevant problems that will be needed, allow individuals to provide feedback to the group, and possibly enable peer observation to guide thinking (Jaworski, 2006).

In conclusion, we can say that the students here were confident that the experience of solving non-routine problems in lectures would be of value to them, both for their current learning and for their future education and careers. Furthermore, they enjoyed the experience and had a positive emotional response to it, which made them feel more capable of solving non-routine problems. That the greatest effect on both self-efficacy and intrinsic interest appeared to be for students with lower prior achievement should add to the appeal of the approach for many institutions, because it has the potential to increase the student retention rate. Overall, the students were emotionally engaged and interested rather than disengaged, which makes them far less likely to drop out of courses (Blondal & Adalbjarnardottir, 2012). All of these positive factors contribute to the strength of the recommendation that other educators give the introduction of this kind of intervention serious consideration.

7. Limitations

One of the key limitations of this research was that it was a reasonably short timescale intervention. More time could not be spent on it, or the PzBL integrated deeper in the courses, since the puzzles were outside of the standard content of all courses. There was also a relatively low response rate (leading to an overall small sample size) despite a very positive attitude of the vast majority of students towards the PzBL intervention and their high level of engagement. Possible reasons for this include the requirement to attend most lectures to be eligible for the study (typical attendance was around 50%), the comprehensive nature of pre- and post-test questionnaires, and the challenging tasks that some students were not confident to do. Due to a small sample size we sometimes were not able to make enough observations to detect significant differences, for example in the parametric test. Another limitation was use of a non-probability sampling—a convenience sampling method with students self-selected for the study was used instead of a random sampling.

Footnote

1. See https://img.scoop.co.nz/media/pdfs/1208/BGAprogressreportbuildinginnovationaugust2012.pdf ↑

 

Acknowledgements

We would like to express our thanks to the Ministry of Education for providing funding through the Teaching and Learning Research Initiative (TLRI) for research such as this to take place. The thoughtful comments and suggestions of the reviewers at the New Zealand Council for Educational Research (NZCER) in response to the milestone reports were beneficial and much appreciated. We are very grateful to our advisory committee members for their valuable feedback at different stages of the project: Professor Glenda Anthony, Professor of Mathematics Education, Co-Director of the Centre for Research in Mathematics Education, Massey University;

Professor Merrilyn Goos, Professor of STEM Education and Director of the National Centre for STEM Education, University of Limerick, Ireland; Professor Barbara Jaworski, Professor of Mathematics Education, Loughborough University, UK; and Fields Medallist Sir Vaughan Jones KNZM FRS FRSNZ FAA, Stevenson Distinguished Professor of mathematics, Vanderbilt University, USA and Distinguished Alumni Professor, University of Auckland.

Research project team

Associate Professor Sergiy Klymchuk, AUT, Principal Investigator.
Emeritus Professor Mike Thomas, University of Auckland, Principal Investigator.

Dr Tanya Evans, University of Auckland, Associate Investigator.
Dr Julia Novak, University of Auckland, Associate Investigator.
Associate Professor Jason Stephens, University of Auckland, Associate Investigator.

Dr Jordan Alexander, AUT.
Professor Sergei Gulyaev, AUT.
Dr William Liu, AUT.
Dr Priscilla Murphy, AUT.

Dr Andrew Zaliwski, Whitireia New Zealand.

Six team members (from the left): Dr William Liu, Professor Mike Thomas, Dr Tanya Evans, Associate Professor Sergiy Klymchuk, Dr Priscilla Murphy, Associate Professor Jason Stephens

Publications and presentations

Evans, T., Klymchuk, S. & Thomas, M. (2018). Puzzle-based learning in university mathematics: students’ perspectives. In Bergqvist, E., Österholm, M., Granberg, C., & Sumpter, L. (Eds.) Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education (PME-42) Vol. 5 (p.46). Umeå, Sweden: PME.

Murphy, P., Evans, T., Klymchuk, S., Novak, J., Stephens, J., Thomas, M. (2020). University STEM students’ perceptions of creativity in non-routine problem-solving. Australian and New Zealand Industrial and Applied Mathematics Journal (ANZIAM Journal), 61 (EMAC2019), C152-C165. https://doi.org/10.21914/anziamj.v61i0.15052

Evans, T., Klymchuk, S., Novak, J., Murphy, P., Stephens, J. M. & Thomas, M. (2020). The impact of non-routine problems on engagement of undergraduate STEM students (Poster Session). The American Educational Research Association (AERA) Annual Meeting. San Francisco, USA: http://tinyurl.com/u2fxpb3

Evans, T., Thomas, M., Klymchuk, S. (2020). Examining STEM employability prospects through the lens of self-efficacy. Higher Education Research and Development (accepted for publication on 3rd August).

Evans, T., Klymchuk, S., Novak, J., Murphy, P., Stephens, J. M. & Thomas, M. (2020). Engagement of undergraduate STEM students: The influence of non-routine problems. Higher Education Research and Development (accepted for publication on 4th September).

Conference Presentations

Unlocking creativity through Puzzle-Based Learning in STEM subjects. Presented by Sergiy Klymchuk at the Computer Science for High Schools Conference (CS4HS), Auckland – Invited talk, 21 November 2018, https://www.cs4hs.aut.ac.nz/

Community of Practice: Embedding Creative Problem Solving into Tertiary Teaching and Learning. Presented by Tanya Evans at the Conference Tertiary Education Research New Zealand, Wellington, 28 November 2018, http://www.herdsa.org.nz/ternz/2018/programme.html

Evaluating the impact of the Puzzle-Based Learning pedagogical strategy in tertiary STEM subjects. Presented by Sergiy Klymchuk and Tanya Evans at the First Year Science Educators’ Colloquium. Auckland – Keynote address, 3 December, 2018, https://atsai4.wixsite.com/fysec2018

Unlocking Creativity through Puzzle-Based Learning in STEM Subjects. Six repeated presentations by Sergiy Klymchuk at the 30th Rotary National Science & Technology Forum held in Auckland, 12– 26 January 2019.

Developing Employability Attributes and Capabilities: Regular Use of Non-Routine Problem Solving in STEM Instruction. Presented by Tanya Evans at the Higher Education Research and Development Society of Australasia Conference (HERDSA), Auckland, 3 July 2019. https://www.herdsa2019.auckland.ac.nz/program/parallel-sessions-day-two/developing-employability-attributes-and-capabilities-regular-use-of-non-routine-problem-solving-in-stem-instruction

Developing Employability Capabilities and Attributes: Regular Use of Non-Routine Problem Solving in Mathematics Instruction. Presented by Tanya Evans at the New Zealand Mathematics and Statistics Education Research Symposium, Wellington, 30 September 2019.

University STEM students’ perceptions of creativity in non-routine problem-solving. Presented by Priscilla Murphy at the International Engineering Mathematics and Application Conference (EMAC-2019), Canberra, Australia, 27 November 2019, https://www.unsw.adfa.edu.au/conferences/EMAC-2019/program

The Impact of Non-Routine Mathematics Problems on Creativity of Undergraduate STEM Students. Presented by Sergiy Klymchuk at the Teachers Calculus Day Conference of the Auckland Mathematical Association, Auckland, 28 November 2019, https://www.aucklandmaths.org.nz/wp-content/uploads/2019/11/Maths-Calc-Day-Programme-19.pdf

Improving Student Engagement – Policy and Practice. Presented by Julia Novak at the New Zealand Mathematical Society Colloquium, Palmerston North, 5 December 2019, https://nzmathsoc.org.nz/downloads/miscellaneous/NZMS_Colloquium_2019_programme.pdf

References

Ahlfeldt, S., Mehta, S., & Sellnow, T. (2005). Measurement and analysis of student engagement in university classes where varying levels of PBL methods of instruction are in use. Higher Education Research & Development, 24(1), 5–20.

Attridge, N., & Inglis, M. (2015). Increasing cognitive inhibition with a difficult prior task: Implications for mathematical thinking. ZDM Mathematics Education, 47(5), 723–734.

Babai, R., Shalev, E., & Stavy, R. (2015). A warning intervention improves students’ ability to overcome intuitive interference. ZDM Mathematics Education, 47(5), 735–745.

Bakker, A. (2018). Design research in education: A practical guide for early career researchers. Routledge.

Barton, B., Oates, G., Paterson, J., & Thomas, M. O. J. (2014). A marriage of continuance: Professional development for mathematics lecturers. Mathematics Education Research Journal, 27(2), 147–164.

Blondal, K. S., & Adalbjarnardottir, S. (2012). Student disengagement in relation to expected and unexpected educational pathways. Scandinavian Journal of Educational Research, 56(1), 85–100.

Burton, L. (1999). Why is intuition so important to mathematicians but missing from mathematics education? For the Learning of Mathematics, 19(3), 27–32.

Cobb, P., Confrey, J., deSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13.

Connell, J. P., & Wellborn, J. G. (1991). Competence, autonomy, and relatedness: A motivational analysis of self-system processes. In M. R. Gunnar & L. A. Sroufe (Eds.), The Minnesota symposia on child psychology, Vol. 23. Self processes and development (p. 43–77). Lawrence Erlbaum Associates, Inc.

Eccles, J., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J., & Midgley, C. (1983). Expectancies, values and academic behaviors. In J. T. Spence (Ed.), Achievement and achievement motives (pp. 75–146). W. H. Freeman.

Falkner, N., Sherwood, R., & Michalewicz, Z. (2012). Teaching puzzle-based learning: Development of basic concepts. Teaching Mathematics and Computer Science, 10(1), 183–204.

Fischbein, E. (1982). Intuition and proof. For the Learning of Mathematics, 3(2), 9–24.

Frederick, S. (2005). Cognitive reflection and decision making. Journal of Economic Perspectives, 19(4), 25–42.

Fredricks, J. A. (2011). Engagement in school and out-of-school contexts: A multidimensional view of engagement. Theory Into Practice, 50(4), 327–335.

Fredricks, J. A., Filsecker, M., & Lawson, M. A. (2016). Student engagement, context, and adjustment: Addressing definitional, measurement, and methodological issues. Learning and Instruction, 43, 1–4.

Gilmore, C., Keeble, S., Richardson, S., & Cragg, L. (2015). The role of cognitive inhibition in different components of arithmetic. ZDM Mathematics Education, 47(5), 771–782.

Guilford, J. P. (1959). Traits of creativity. In H. H. Anderson (Ed.), Creativity and its cultivation (pp. 142–161). Harper & Brothers.

Guilford. J. P. (1967). Creativity: Yesterday, today and tomorrow. Journal of Creative Behaviour, 1(1), 3–14.

Hatano, G., & Oura, Y. (2003). Commentary: Reconceptualizing school learning using insight from expertise research. Educational Researcher, 32(8), 26–29.

Helme, S., & Clarke, D. (2001). Identifying cognitive engagement in the mathematics classroom. Mathematics Education Research Journal, 13(2), 133–153.

Jaworski, B. (2006). Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. Journal of Mathematics Teacher Education, 9(2), 187–211.

Jaworski, B., Robinson, C., Matthews, J., & Croft, T. (2012). An activity theory analysis of teaching goals versus student epistemological positions. International Journal of Technology in Mathematics Education, 19(4), 147–152.

Kahu, E., & Nelson, K. (2018). Student engagement in the educational interface: Understanding the mechanisms of student success. Higher Education Research & Development, 37(1), 58–71.

Klymchuk, S. (2001). Money puzzles: On critical thinking and financial literacy. Maths Press.

Klymchuk, S. (2017). Puzzle-based learning in engineering mathematics: Students’ attitudes. International Journal of Mathematical Education in Science and Technology, 48(7), 1106–1119.

Klymchuk, S., Thomas, M., Gulyaev, S., & Evans, T. (2017). Enhancing generic thinking skills of tertiary STEM students through puzzle-based learning. Ako Aotearoa. https://ako.ac.nz/assets/Knowledge-centre/RHPF-N70-Puzzle-based-learning/de81124b09/RESEARCHREPORT-Enhancing-Generic-Thinking-Skills-of-Tertiary-STEM-Students-through-Puzzle-Based-Learning.pdf

Leikin, R. (2009). Exploring mathematical creativity using multiple solution tasks. In R. Leikin, A. Berman, & B. Koichu (Eds.), Creativity in mathematics and the education of gifted students (pp. 129–145). Sense Publishers.

Leikin, R., & Pitta-Pantazi, D. (2013). Creativity and mathematics education: The state of the art. ZDM Mathematics Education, 45(2), 159– 166.

MacLeod, C. M. (2007). The concept of inhibition in cognition. In D.S. Gorfein & C. M. MacLeod (Eds.), Inhibition in cognition (pp. 3–23). American Psychological Association.

Michalewicz, Z., & Michalewicz, M. (2008). Puzzle-based learning: An introduction to critical thinking, mathematics, and problem solving. Hybrid Publishers.

National Survey of Student Engagement. (2000). Improving the college experience: National benchmarks of effective educational practice. Indiana University Center for Postsecondary Research and Planning.

New Zealand Ministry of Research, Science and Technology (2007). Vision mātauranga. Author. https://www.mbie.govt.nz/ dmsdocument/1269-vision-matauranga-booklet

Parhami, B. (2008). A puzzle-based seminar for computer engineering freshmen. Computer Science Education, 18(4), 261–277.

Poundstone, W. (2000). How would you move Mount Fuji? Microsoft’s cult of the puzzle—How the world’s smartest companies select the most creative thinkers. Little Brown and Company.

Prediger, S., Gravemeijer, K., & Confrey, J. (2015). Design research with a focus on learning processes: An overview on achievements and challenges. ZDM Mathematics Education, 47(6), 877–891.

Ryan, A. M. (2000). Peer groups as a context for the socialization of adolescents’ motivation, engagement, and achievement in school. Educational Psychologist, 35(2), 101–111.

Selden, A., Selden, J., Hauk, S., & Mason, A. (2000). Why can’t calculus students access their knowledge to solve nonroutine problems? In E. Dubinsky, A. Schoenfeld, & J. Kaput (Eds.), Research in collegiate mathematics education: IV. Issues in mathematical education (Vol. 8, pp. 128–153). American Mathematical Society.

Sriraman, B., & Haavold, P. (2016). Creativity and giftedness in mathematics education: A pragmatic view. In J. Cai (Ed.), First compendium for research in mathematics education. National Council of Teachers of Mathematics. Available from http://hs.umt.edu/math/research/ technical-reports/documents/2016/03_SriramanHaavold.pdf

Thomas, C., Badger, M., Ventura-Medina, E., & Sangwin, C. (2013). Puzzle-based learning of mathematics in engineering, Engineering Education, 8(1), 122–134.

Thomas, M. O. J. (2004, 4–11 July). Conceptual representations and versatile mathematical thinking. Proceedings of ICME-10 (CD version). The 10^th International Congress on Mathematical Education. Copenhagen, Denmark. Available from [https://www.researchgate.net/profile/Michael_Thomas10/publication/236131562_Conceptual_representations_and_versatile_mathematical_thinking/ links/0deec53b130be4b890000000/Conceptual-representations-and-versatile-mathematical-thinking.pdf]

Thomas, M. O. J. (2008). Developing versatility in mathematical thinking. Mediterranean Journal for Research in Mathematics Education, 7(2), 67–87.

Thomas, M. O. J. (2015). Inhibiting intuitive thinking in mathematics education. ZDM Mathematics Education, 47(5), 865–876.

Torrance, E. (1963). Education and the creative potential. University of Minnesota Press.

Trémolière, B., & Neys, W. (2014). When intuitions are helpful: Prior beliefs can support reasoning in the bat-and-ball problem. Journal of Cognitive Psychology, 26(4), 486–490.

Wallas, G. (1926). The art of thought. Harcourt, Brace & Company.

Watt, H. M. G., & Goos, M. (2017). Theoretical foundations of engagement in mathematics. Mathematics Education Research Journal, 29, 133–142.

Wigfield, A., & Eccles, J. S. (2000). Expectancy-value theory of achievement motivation. Contemporary Educational Psychology, 25(1), 68–81.

The appendices for this online version of the report have been removed. However, you can access them here