1. Introduction – Mathematics: She’ll be write!
How students learn to speak, read, and write science and mathematics, and what is taking place in the classroom, laboratory, or informal learning context are critical areas for research. (Lerman, 2007, p. 756)
The focus of this Teaching and Learning Research Initiative (TLRI) project was to discover effective ways to develop students’ mathematical writing in te reo Māori. It was assumed that this would lead to better understanding of mathematics. The investigation was undertaken at Te Kura Kaupapa Māori o te Koutu which caters for students from Years 0–13, many of whom are second language users of te reo Māori. It involved all the teachers as well as two outside researchers considering a number of issues around the role of writing in mathematics.
Investigating the provision of professional development of effective ways to support students’ mathematical writing is an area in which very little research has been done previously (see Doerr & Chandler-Olcott, in press, for the exception). Consequently, this research report should not be seen as describing completed work, but rather as a snapshot of where we have travelled up to this point, in regard to the integrated, intricate nature of teacher professional development to improve student achievement. It was ethnographic research that was bounded by being conducted in one kura, where the language of instruction in mathematics was te reo Māori. The context as well as a detailed description of the research process undertaken by the teachers and other researchers is provided, so that our results and analysis can be better understood by others who may share some or none of the characteristics of the situation.
As a consequence of the research, a variety of different genres and text types were identified. The genres identified by the teachers were: whakaahua; whakamārama; and parahau. These have been organised in progressions showing how different layers of meaning are added to the text types. Using this information, we then explored how students could be supported to use writing to help their thinking processes and thus their mathematical learning. Various strategies were trialled by teachers and some of the results of these are discussed in this report. It was quite clear that both the amount and variety of writing done in all classes increased as a result of the teachers being involved in the project. The project used a Teacher Inquiry and Knowledge Building Cycle (Timperley, Wilson, Barrar, & Fung, 2007) approach that concentrated on developing programmes based on the identified learning needs of students and teachers. A fundamental component of this approach was the integration of reflection with action, which is also known as praxis.
This project built on an earlier TLRI project. In that project, Te Kura Kaupapa Māori o te Koutu’s teachers and the research team worked together in 2005 and 2006 to identify the teaching strategies that were effective for developing students’ use of te reo tātaitai or the mathematical terms and expressions within te reo Māori (Meaney, Fairhall, & Trinick, 2007). As a result of this project, teachers became aware of their need to concentrate more specifically on the teaching of mathematical writing. This is a need that has been recognised in many countries for some time (Ntenza, 2006). The results of this research, therefore, have implications not just for other kura kaupapa Māori but also for schools and mathematics teachers throughout the world.
An emphasis on mathematical communication is clearly indicated in the English- and Māori- medium curriculum statements (Ministry of Education, 1992, 1993). The document states that there will be opportunities provided “for students to develop the skills and confidence to use their own language, and the language of mathematics, to express mathematical ideas” (p. 9). The importance of language in helping children make sense of their world is supported by Campbell and Rowan (1997) who assert that “language has the power to help children organize and link their partial understandings as they integrate and develop mathematical concepts” (p. 64).
The teaching approaches recommended by the national curriculum statement (Ministry of Education, 1994) are, at heart, constructivist. The constructivist view is that people make “sense of the world in ways that are always historically and culturally specific” (Begg, 1999, p. 5). For students to be able to succeed in mathematics, they need to use mathematical language to help them make sense of the learning situation, rather than merely being expected to solve problems in the manner in which they have been shown. Developing a shared meaning of mathematical ideas is a key process within constructivist learning theory (Good & Brophy, 1990). This means that children should have the ability to verbalise someone else’s understandings to themselves so that they can reorganise external language into an “inner language” or “internalised thought”.
Within the field of mathematics education, there seem to be a number of issues relating to the forms of communication expected of students. Underlying these issues, though, is the expectation that children need to communicate effectively. Sfard, Nesher, Streefland, Cobb, and Mason (1998) stress the importance of developing children’s communication skills but question how this will be done and what should actually be taught, and comment that this is an issue that has not really been given much thought by the mathematics education community. They argue that children need to be taught how to communicate with their peers and teachers so that there is a base line of shared understanding.
A focus on how to support students’ writing in mathematics was chosen because it was believed that it would improve students’ reflection on their mathematical thinking (Southwell, 1993). The kura’s involvement in Poutama Tau, the New Zealand numeracy professional development project for teachers in Māori-medium classrooms, had meant that there was an awareness of the need to have students explain their thinking. Analyses of the Te Poutama Tau student data found that language proficiency was a significant factor in student achievement in the higher stages of the number framework (Christensen, 2003). In order for students to communicate mathematically in Māori medium, there is a need for the teaching community to understand what effective mathematical communication looks and sounds like in the classroom.
The effects of language learning on mathematics have been recognised for some time (Ellerton & Clarkson, 1996) but minimal research has been carried out on how students acquire the mathematical register. Although communication of all kinds is supposed to support students’ thinking mathematically (National Council of Teachers of Mathematics, 1989), writing, because it can be referred to again and again, supports the reflection process more easily than spoken language (Albert, 2000):
Writing is a valuable way of reflecting on and solidifying what one knows, and several kinds of exercises can serve this purpose. For example, teachers can ask students to write down what they have learned about a particular topic or to put together a study guide for a student who was absent and needs to know what is important about the topic. A student who has done a major project or worked on a substantial long-range problem can be asked to compare some of their early work with later work and explain how the later work reflects greater understanding. In these ways, teachers can help students develop skills in mathematical communication that will serve them well both inside and outside the classroom. Using these skills will in turn help students to develop deeper understandings of the mathematical ideas about which they speak, hear, read, and write. (National Council of Teachers of Mathematics, 2000, p. 352)
Research by Pugalee (2004) showed that students who wrote descriptions of their thinking were significantly better able to solve mathematical problems than those who verbalised their thinking processes. One of our underlying assumptions about increasing the quantity and quality of students’ writing was that it would lead to improvements in students’ understanding of mathematics.
The importance of students being able to explain their thinking process is also valued in New Zealand’s formal assessment processes. The National Certificate of Educational Achievement (NCEA) in mathematics requires students to be able to write explanations and justifications (Meaney, 2002a). The teachers at te Koutu believed that it was in the junior classes that students should start developing these skills and that there needed to be a coherent approach across the kura to the teaching of mathematical writing. This matched what Hipkins and Neill (2006) wrote about the impact of NCEA on high school mathematics teachers’ awareness about language:
both mathematics and science teachers give a relatively high priority to the need to develop language and literacy practices associated with each discipline. In at least two cases the teachers’ awareness of these issues has been sharpened by participation in school-wide literacy initiatives. (p. 63)
Having students write can also support teachers to understand better students’ mathematical misconceptions as it often provides the teachers with more information than what is gained from simply listening to students (Drake & Amspaugh, 1994). We wanted to investigate writing both as a way of supporting students’ mathematical thinking and also as a means by which teachers could better understand their students’ knowledge of mathematics.
The mathematics register in English makes use of the passive voice and logical connectives (Meaney, 2005a). As both of these are prominent features in traditional oral reo Māori, the teachers were also interested in exploring whether mathematics could be a vehicle for improving students’ reo Māori language skills in general. In the previous TLRI project (Meaney et al., 2007), we found that te reo Māori had many more logical connectives than English. Therefore, we also wanted to explore how providing students with information about using these logical connectives could support their mathematical thinking. Writing can more easily be used in explicit language learning as it can be referred to time and time again. However, there was concern about how a concentration on writing might result in a devaluation of speaking.
Orality and literacy
Te reo Māori has a long oral tradition and a concentration on writing must be considered within this context. Western beliefs about the value of writing in improving students’ thinking processes as propagated by researchers such as Vygotsky and Luria (Gee, 1989) cannot take precedent over issues relating to the how and why of teaching mathematical writing in the immediate situation of a kura kaupapa Māori. Although literacy is believed to have a role in the regeneration of a language (Hohepa, 2006), concern has also been raised about the possible imposition that writing can have on Indigenous communities’ ways of being (Cavalcanti, 2004; Street, 1995). Gee (1989) stated that:
Discourse practices are always embedded in the particular world view of a particular social group; they are tied to a set of values and norms. In learning new discourse practices, a student partakes of this set of values and norms, this world view. Furthermore, in acquiring a new set of discourse practices, a student may be acquiring a new identity, one that at various points may conflict with the student’s initial acculturation and socialization. (p. 59)
As a discursive practice, mathematical writing will have an impact on students’ identity. Whether this identity forming will be in conflict with the students’ Māori identity will depend on how the discursive practices are taught. In kura kaupapa Māori, “the pedagogy of these schools is based on, but not exclusively, Māori preferred teaching and learning methods” (Smith, 1990, pp. 147–148). It was, therefore, important that the role of writing in the teaching and learning of mathematics was not just accepted without question. With te reo Māori still in a process of regeneration after almost becoming extinct in the 1970s, there was a need to consider how the teaching and learning of writing in mathematics could be done in a culturally appropriate way. In discussing the role of reading in the home, Hohepa (2006) wrote:
A significant issue in the context of language regeneration concerns how language practices both reflect and construct cultural concepts and values. One way to address this issue is to ensure that ways of carrying out an activity such as book reading do not undervalue or replace existing cultural ways but are added to family repertoires (McNaughton, 1995). Also, ways of participating in the activity which are not inconsistent with the specific literacy goals, but which are consistent with culturally preferred ways of participating can be promoted. (p. 299)
Hohepa’s warning can also be related to mathematical writing. The advantages for students’ mathematical learning in being able to write mathematically had to be considered in relationship to other priorities that the kura and its whānau had for students. Issues of spoken mathematical language cannot be divorced from considerations of how to effectively teach writing in mathematics. As well, questions such as “What is writing in mathematics?” and “What constitutes an appropriate mathematical written text?” need to be situated in the wider context of this kura kaupapa Māori’s aspirations for its students.
What is writing in mathematics?
One of the first ideas that we had to determine was what it was that we, as teachers and researchers, meant when we referred to mathematical writing. In our original research applications, we had made reference to diagrams and models as also being examples of mathematical writing. Given that meaning is produced in mathematics through a variety of different written forms (O’Halloran, 2000), it was important to consider the relationship between the situations in which the writing was produced and the impact of the audience on the writing. The act of writing needed to be situated in the context that it was written in, thus acknowledging the impact of the social environment on the piece of writing that was produced (Gibbons, 1998). These were vital considerations given the situation in which we were investigating the teaching and learning of mathematical writing. Consequently, our beliefs about what constitutes writing in mathematics are discussed using Halliday’s ideas about context of culture and context of situation (Halliday & Hasan, 1985).
Using the ideas of the anthropologist Malinowski, Halliday described how a text or piece of language “that is functional” (Halliday & Hasan, 1985, p. 10) is both a process and a product that reflects the wider cultural background as well as the immediate situation in which it arises. The meaning that is conveyed by a text is influenced by both the context of culture and the context of situation. Linguistic choices are made by the producers of the text that illustrate their perceptions of the context of situation, often unconsciously (Meaney, 2005a). Figure 1 shows how Halliday (Halliday & Hasan, 1985) views the relationship between linguistic choices and the context of situation.
Figure 1 Relations of the text to context of situation (from Halliday & Hasan, 1985, p. 26)
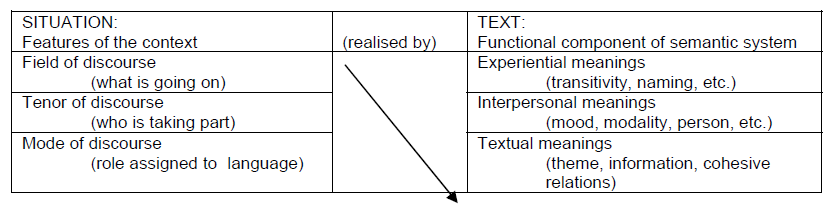
Therefore, by looking at the linguistic choices used in a piece of mathematical writing it would be possible to see the producer’s perception of the context of situation. Another way of perceiving this set of relationships is shown in Figure 2.
However, viewing mathematics symbolism and other visual representations as language that can be analysed is a contentious issue. Halliday (2007) expressed doubts about whether mathematics could be analysed for meaning in the same way that texts that used words could be. He stated that “[m]athematics is not, of course, a form of visual semiotic, but it is expressed in symbols that look like, and in some cases are borrowings of, written symbols . . . We cannot read it, because it has no exact representation in wording” (p. 114). He went on to state that it could be verbalised in a range of equivalent mathematical forms but which were grammatically quite different and this would affect the meaning that was given to them. Halliday wrote how he would not describe these visual representations of information such as graphs as language: “they are semiotic systems whose texts can be translated into language, and that offer alternative resources for organizing and presenting information” (p. 115).
Figure 2 A model showing how language acts as a viaduct between culture and understanding (from Meaney, 2005a, p. 113)
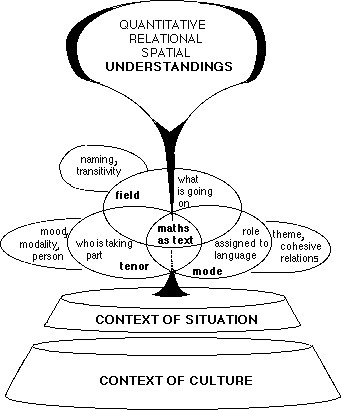
As a result of the ambiguity that arises when interpreting mathematical symbols and other visual representations, Halliday would not refer to anything but written words as constituting a piece of writing. However, other researchers have not agreed with Halliday’s refusal to consider mathematics as something that can be analysed in the same way as language (see, for example, Kress & van Leeuwen, 2006). Several have used Halliday’s systemic functional grammar to describe how meaning is produced and interpreted in other forms than just words (Unsworth, 2001). O’Hallohan (2000) who applied systemic functional grammar to discourse in mathematics classrooms stated:
mathematics is construed through the use of the semiotic resources of mathematical symbolism, visual display in the form of graphs and diagrams, and language. In both written mathematical texts and classroom discourse, these codes alternate as the primary resource for meaning, and also interact with each other to construct meaning. (p. 360)
In this project, we have followed this tradition and have taken a broader definition of mathematical writing. Without acknowledging the multiple representations that could be used in mathematical writing, there would be very few mathematical pieces of writing that could be analysed. Nevertheless, it was important to note Halliday’s (2007) warning that there is a need to be aware of “meanings being lost, and what new meanings imposed, when there is translation between verbal and the non-verbal; and exploring the semiotic potential that lies at their intersection” (p. 116). Everyone will interpret a piece of writing in a variety of ways because they come to the piece of writing with different backgrounds. However, in interpreting mathematical symbols and visual displays, greater differences in interpretation may arise. It is therefore important to think carefully about how to support students developing a range of different visual information displays in mathematics so that shared meanings arise from this process.
The development of pieces of writing occurs within what has been defined as “literacy events”. Heath (1982) described these as “any occasion in which a piece of writing is integral to the nature of participants’ interactions and their interpretive processes” (p. 93). It is, therefore, important to consider how the context in which the writing is done will affect its form and appropriateness.
Appropriateness of pieces of writing
In considering effective ways to support students’ mathematical writing, it is important to have some understanding about what kinds of writing we are expecting students to use, as well as knowledge about how to support students to judge the quality of their own writing. In Chapter 5 of this report, we describe the teachers’ views about a good piece of writing. However, there is a need to consider what constitutes an appropriate piece of writing and how this may differ from good writing. This is an important distinction because appropriateness deals with whether the piece of writing achieved its purpose or function. On the other hand, discussions about quality or “good writing” assume that the function has been achieved, but distinctions can be made about the clarity or conciseness or some other criteria and the impact that this has on the quality of the piece of writing.
In considering the appropriateness of the writing, considerations revolve around whether the linguistic choices match the field, tenor and mode of the context of situation. In order to reflect the meanings available within the field, does the author of the piece of writing make clear the “kind of acts being carried out and their goal(s)” (Halliday & Hasan, 1985, p. 56)? How are the participants (including inanimate participants) labelled or highlighted and what are the types of verbs or processes that are used? The amount of detail as well as the choice of vocabulary will be affected by the situation. If the student is using writing to work something out, it is likely to be less explicit and much messier than writing that is for formal display (Ernest, 2007). There has been discussion about the role of formal mathematics terms in the learning of mathematics (Leung, 2005). Barnes (1976) identified distinct features of “exploratory talk” and “final draft talk” and a similar set of features could be identified with mathematical writing done as part of the process of thinking as opposed to writing done for formal presentation. Of course, the different audience, self as opposed to examiner, would have an impact on this writing. This is discussed in more detail in Chapter 3.
The interpersonal meanings realised through the tenor reflect the relationship between the author and the reader. Hasan described how the social distance between participants “affects styles of communication” (Halliday & Hasan, 1985, p. 57). When the participants are not familiar with each other, such as when a student is writing an exam paper, then there is a need for more explicitness than if the participants have a longstanding relationship such as when a student writes for their teacher. Morgan (1998) identified six audiences that students may write for in a mathematics lesson, including an indiscernible audience.
The mode shows how the type of writing, graphs, symbols and so on affects the textual meanings that are produced. Information presented in words as opposed to being presented in a graph will be interpreted differently by an audience. This is because the different types will highlight some aspects of the information while downplaying others. These aspects will differ depending upon the type of writing that is used.
For students to produce an appropriate piece of writing, they need to show an awareness of how changes in field, tenor and mode affect how they present their mathematical meaning. In Chapter 3, we describe what this may mean in regard to the pieces of writing that were collected during the project and how this relates to evaluations of the quality of individual students’ pieces of writing.
Report overview
This report consists of nine chapters and these are briefly described below. As the findings presented in Chapters 3 to 8 are quite distinct, rather than having one literature chapter, previous relevant research is described at the beginning of each of these chapters.
Chapter 2: Research methodology
This chapter outlines how we used a case study approach. It also describes the data that we collected.
Chapter 3: Genres
This chapter describes how students’ pieces of writing were classified according to their function: whakaahua; whakamārama; parahau. These categories were then related to Halliday’s ideas about field, tenor and mode within a context of situation.
Chapter 4: Whakaahua
The progressions for the different topics of descriptions are discussed. An initial explanation of how these types of descriptions are related to the year-level progressions is also given.
Chapter 5: Whakamārama me parahau
This chapter looks at the explanations and justifications in the set of writing samples and explores how different text types are often integrated to produce these genres. It also discusses the teachers’ perspectives on the benefits for writing as well as what constitutes a “good” piece of mathematical writing.
Chapter 6: Ways to improve mathematical writing
This chapter discusses how teachers facilitated students’ writing about mathematics. It describes acts of writing and the strategies that the teachers used to help students acquire mathematical writing. It provides a matrix to show how acts of writing, mathematics register acquisition (MRA) model strategies and genres are connected.
Chapter 7: Student writing
This chapter describes the typical writing done by students at the different year levels. We look specifically at the writing done around probability at the different year levels. This was connected to students’ beliefs about writing in mathematics, gathered through surveys and interviews. These beliefs, including the older students’ beliefs about completing bilingual exams, are described here.
Chapter 8: Teacher change
The effect of participating in this project on teachers’ teaching practices and their ability to reflect on their own learning are discussed in this chapter. It shows that all the teachers felt that their changes in practices had increased the quantity and/or the quality of students’ writing in mathematics.
Chapter 9: Conclusion
This chapter summarises the major findings and provides a discussion of the implications for this kura and for other mathematics classrooms. It also reflects on the limitations of the project and further research that this kura wishes to undertake.
2. Genres
One of the aims of the project was to describe the types of writing that students were currently using at the kura and then look at ways to improve both the quality and the quantity of the pieces of writing at all year levels. Little previous research had been done in this area and so there was little guidance on how to do this. Although curriculum documents emphasised the need for students to learn the language of mathematics, there were rarely specific examples of how to do this. For example, Doerr and ChandlerOlcott (in press) described how the National Council of Teachers of Mathematics (2000) Standards provided “limited discussion of different genres of mathematical writing that students might engage with and how they might learn to attend to audience and purpose in each of those genres and how these, in turn, might vary across mathematical tasks and grade level”.
At the research report meeting held in 2006 to set the parameters for what would be done in the She’ll be Write! project there was a sharing of anecdotal stories about students’ mathematical writing. For example, at the senior level of the kura it was felt that students did not want to elaborate on their explanations but rather kept them short, using simple language that they felt most comfortable with. Mathematical language was used only because students believed that teachers expected them to use it. This belief is similar to those given by students in Healy and Hoyles’s (2000) research on students’ development of proofs.
By systematically collecting and analysing students’ pieces of writing, it was felt that a better understanding could be gained about whether other, more appropriate types of writing could be introduced to students and how the ones that were currently being used could be improved so that students’ learning of mathematics and te reo Māori could be supported (Meeting 30 August 2006). One way of analysing the pieces of writing was to classify them into different genres and then to identify the features of each of the genres. This chapter provides a description of the different genres that were identified at the kura and their relationship to Halliday’s field, tenor and mode. Chapters 4 and 5 provide more details of the different genres.
What are genres in mathematics classrooms?
Any text, whether oral or written, is influenced by three components. These are: what is being discussed; who is involved in the text (producing it, interpreting it or within it); and the form the communication is taking (written, oral, gestures). Halliday described these as field, tenor and mode (see Meaney, 2005a). Changes to any of these will result in changes to the text that is produced (Halliday & Hasan, 1985). Consequently, types of texts will reflect the purposes that they serve in meeting the requirements of these three components. For example, demographic data are commonly presented in graphs, especially if they are going in reports designed for statistically literate adults.
If texts are continually produced to fulfil the same set of field, tenor and mode requirements, then their linguistic and other features will become stabilised over time. However, the inclusion of new features will continue to occur and so description of the features of genres should not be considered as rigidly fixed. Stabilisation occurs as a result of “negotiation among and between community members” (Wallace & Ellerton, 2004, p. 8). As a result of this stabilisation of features, sets of texts can be categorised as genres. To not structure the texts that are responding to the same set of field, tenor and mode in the conventional way can result in the meaning that is supposed to be produced being misinterpreted (Huang & Normandia, 2007). It is, therefore, important that students learn during their schooling experiences how to write the genres that are used in particular content areas (Unsworth, 2001). Knowing about genres is not just knowing what features to include but also knowing how and when genres are useful. As Pimm and Wagner (2003) wrote “[m]uch of this work (e.g. Martin, 1989; Halliday & Martin, 1993) is also rooted in questions of school systems developing greater equity by means of students gaining access to linguistic-cultural capital” (p. 162). For the students at the kura, it is valuable to understand the role of genres in mathematics. They can take this knowledge about genres with them if they go on to study further mathematics at university in English or another language. However, investigation of this would be for a future project and is not considered here. In this project, the purpose of identifying the genres was to have a starting point for teachers to consider how to improve the quality and quantity of students’ mathematical writing.
What is the relationship between the mathematics register and genres?
In discussing genres, there is a need to distinguish them from registers (Wallace & Ellerton, 2004). In this research report, we have used definitions more closely aligned with those of Halliday than those given in Wallace and Ellerton (2004). In every mathematics classroom, there would be a number of different genres. Some of these genres would be common across many classrooms. These would have a set of distinctive features that are organised into a specific structure and they all fulfil a certain function (Unsworth, 2001). However, if they were identified as mathematical genres then they would contain certain vocabulary and grammatical expressions that would support the mathematical meanings being presented. These texts would use the vocabulary and grammatical expressions of the mathematics register. Halliday described registers as:
the semantic configurations that are typically associated with particular social contexts (defined in terms of field, tenor, and mode). They may vary from ‘action-orientated’ (much action, little talk) to ‘talk-orientated’ (much talk, little action). (Halliday & Hasan, 1985, p. 43)
Consequently, aspects of the mathematical register would be apparent in all mathematical genres.
Mathematical genres
Although genres have received significant amounts of attention since the 1980s, especially in Australia and the United Kingdom (Unsworth, 2001), very little research has been done in regard to those typically found in mathematics classrooms. Like Morgan (1998), Marks and Mousley (1990), using the ideas of Martin (1985/1989), identified several genres that mathematicians would use and that, therefore, should be included in students’ repertoire of mathematical writing. These genres were:
Procedure: how something is done
Description: what some particular thing is like
Report: what an entire class of things is like Explanation: reason why a judgement has been made
Exposition: arguments why a thesis has been produced.
However, when they investigated the genres which were used in 11 classrooms (seven primary and four secondary), they found many instances of recounts, incorporating symbols and visual representations, but very few examples of other genres. Recounts described what a student had done during a mathematical activity and is generally expressed as a narrative. This would suggest that these students were not learning the conventions associated with mathematical writing because “mathematics cannot be narrative for it is structured around logical and not temporal relations” (Solomon & O’Neill, 1998, p. 217). In stories, cohesion is achieved by placing a series of events in a timeline. In mathematics, cohesion is achieved by relating separate ideas through logical connections. These relationships are timeless and therefore using time markers as is common in recounts is inappropriate in discussing mathematics.
Given that the purposes for writing are different for mathematicians than they are for students, it is perhaps not that surprising that students were being asked to write different kinds of genres. However, by the time students are in their final years of high school it could be expected that the students would have the skills to produce many of the genres used by mathematicians. It would be anticipated that some of these genres or early versions of these genres should be presented in all mathematics classrooms.
We were interested in considering what genres the students at the kura were using and how these related to those outlined by others such as Marks and Mousley (1990). Given that our purpose for categorising students’ pieces of writing was so that it could be a base for considering how to improve the quality and quantity of this writing, it was anticipated that our genres would be different from those of others.
What we did and what we found
The investigation of the students’ pieces of writing was done by the teachers with the researchers. It, therefore, must be considered as being at the second tier of the research model proposed by Doerr and Chandler-Olcott (in press) for investigating writing in mathematics classrooms that was described in the previous chapter.
At a meeting in March 2007, the teachers were provided with a variety of pieces of mathematical writing that had been collected during the previous year. These were classified by teachers, first in pairs and then as a whole group. Much of what is reported in the following paragraphs comes from the minutes of the meeting. The teachers classified the writing into three genres and an initial set of modes. Many of these categorised pieces of writing had been collected at the end of 2006. Over the course of 2007, other pieces of writing were collected. All writing samples were scanned, classified according to genre and mode and then named and filed.
Although the genres remained set, there were changes to how the modes were identified as more pieces of writing were added to the database. As Unsworth (2001) wrote “[g]enres are not fixed and invariant. They identify classes of texts with particular characteristics in common . . . Genres, as integral features of subject area learning and teaching, then, should not be considered as straitjackets but as starting points” (p. 127). It was important to our project to have relevant labels for the categories we identified. There was considerable discussion about these at the March 2007 meeting. The labels were: whakaahua (description); whakamārama (explanation); and parahau (justification).
In this section, we briefly discuss the genres and then the modes. The following section considers how changes to the field, tenor and mode would impact on the types of writing produced. The features of the genres are described in more detail in Chapters 4 and 5.
First, we need to acknowledge the limitations of our database of pieces of writing. Although more than 2,000 pieces of writing were collected, the database is still incomplete. The junior section of the kura runs a two-year cycle for their mathematics programme and so not all strands and topics were covered in 2007. In the senior part of the kura, the teachers taught multiple mathematics classes. For this project each teacher focused on only one of their classes. Consequently, few, if any, samples were collected from Years 9, 10, 12 and 13. As well, the primary researcher who collected the pieces of writing, did so during her once-a-term visits to the kura. During these visits, pieces of work were not always collected from the teachers, sometimes because a teacher was away or because writing had been part of a classroom display that was no longer available. Nevertheless, the database is extensive and does show a range of writing done in mathematics classrooms.
Three distinct genres were identified by the teachers and these can be seen in Table 2. The process used to do this classification was for each pair of teachers to look over a range of students’ pieces of writing. The samples came from students of different ages and were from a range of topics. The quality of the writing also varied. In pairs, the teachers classified the students’ writing according to categories that they felt were appropriate. Two pairs then shared their categories and decided on a joint set of categories. Then the whole group came together and had a more extended discussion about the genres. The teachers focused on grouping samples of writing that appeared to have the same function. They, therefore, identified the primary purpose of each piece of writing and then looked at the structure within each group. It was at this point that the genres were separated from the modes and Table 2 was developed.
Table 1 Writing genres and their modes
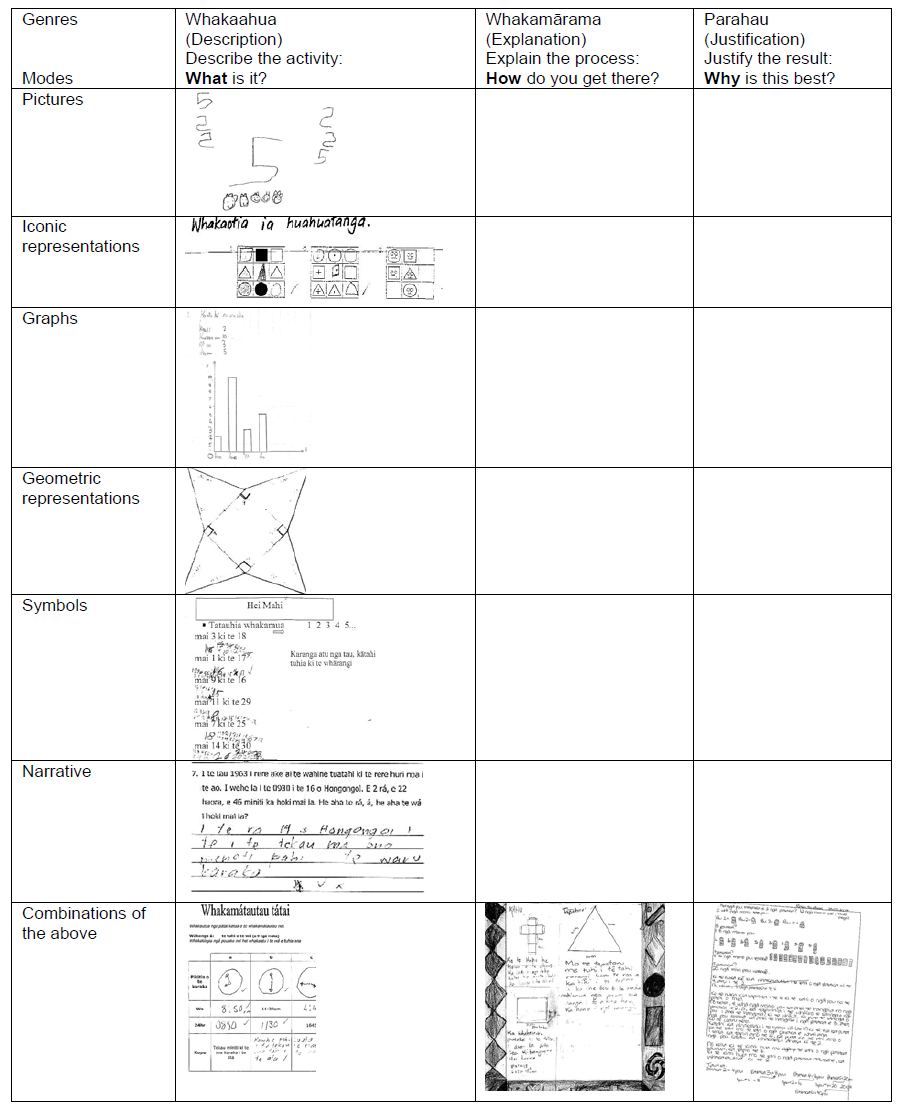
The modes of writing that students used in the genres were: pictures; iconic representations; graphs; geometric representations; symbols; and narratives. Other researchers had sometimes considered what we had labelled as modes to be genres. Solomon and O’Neill (1998) stated that “[i]n so far as genre shapes and constrains the nature of a text, then graphs, equations, proofs and algorithms can be considered as expressions of genre” (pp. 217–218). However, our definition of genre was based on the function that it performed and therefore the channel through which the function is delivered was considered to be the mode. Other researchers in semiotics used the term registers for different representations of mathematical ideas (Gagatsis, Elia, & Mousoulides, 2006). Duval (2002) identified four types of representation register: “natural language; geometric figures, notational systems and graphic representations” (cited in Gagatsis et al., 2006). These were similar to our modes of narratives, geometric representations, symbols and graphs in Table 2.
Ben-Chaim, Lappan, and Houang (1989) described three modes that were used by students in descriptions of an object made from cubes taped together. These modes were: verbal; graphic; and mixed mode. The verbal mode occurred when the student’s message was carried by words. A diagram might accompany the words but did not add any more meaning to what was stated in words. A graphic mode used drawings with, at the most, labels to accompany it. A mixed mode used both diagrams and words to convey meaning. As can be seen in Table 3, we collected a variety of pieces of mathematical writing and so had a larger number of modes. This larger number of modes also meant that we had to choose a greater number of labels and thus there was a need to move beyond those suggested by Ben-Chaim et al. (1989).
Although in Ben-Chaim et al.’s (1989) study, the graphic mode was believed to be the more successful at accurately conveying information about the object, the teachers felt that, commonly, genres would require a combination of modes rather than being exclusively one or the other. This belief is supported by O’Halloran (2000) who wrote:
Mathematics is not construed solely through linguistic means. Rather, mathematics is construed through the use of the semiotic resources of mathematical symbolism, visual display in the form of graphs and diagrams, and language. In both written mathematical texts and classroom discourse, these codes alternate as the primary resource for meaning, and also interact with each other to construct meaning. Thus, the analysis of ‘mathematical language’ must be undertaken within the context of which it occurs; that is, in relation to its codeployment with mathematical symbolism and visual display. (p. 360)
The genres were chosen because they fulfilled different functions. One was to describe, the next to explain and the final one was to justify. Although these categories were broader than those used by others in categorising mathematical genres (Marks & Mousley, 1990), it was still difficult at times to decide which of these genres a piece of writing should be categorised as. For example, a piece of writing could begin by describing something but finish by explaining something else. However, the component parts constitute the whole and could not be separated. An example of this can be seen in Figure 4. If this was the situation, then the piece of writing was categorised in the higher level, in this case the explanation.
Figure 3 ECKaL3 showing a combination of description and explanation

ECKaL3 starts with a description using symbols of the various combinations that different numbers and colours of blocks could form. It ends with an explanation of the equation relating the number of combinations to the number of blocks and the number of colours.
Whakaahua
Whakaahua was the label given to pieces of writing that described something. A range of these can be seen in Table 2. Writing descriptions provided students with opportunities to learn the conventions of mathematical writing. The descriptions could be in words, but could also be a numerical fact written in symbols. Descriptions of this kind have been classified as other things by different researchers. Marks and Mousley (1990) would separate out descriptions from reports whereas whakaahua contained both. Wallace and Ellerton (2004) stated that:
Description and report genres provide the nature of individual things and the nature of classes of things, respectively. Reports are characterised by generic participants, simple present-tense verbs, and a large percentage of ‘being’ and ‘having’ clauses (p. 9)
As more samples were collected and added into our classification system, it became clear that a defining characteristic for us of whakaahua was the way that new information was added. In systemic functional grammar, the way that new information is juxtaposed with given information is an important part of the construction of meanings in texts (Unsworth, 2000). If the addition of new information was cumulative (this is a triangle, it has three sides and it has three angles), or if new information could not be added without changing the function, then the piece of writing could be classified as whakaahua. Thus, equations such as 3 + 4 = 7 could be classified as a description because adding new information such as (3 x 1) + (2 x 2) = 9 – 2 actually changes the function of the equation from merely describing a simple fact to showing how each term has other ways of being described and that it is the combination of these descriptions that shows a deeper level relationship between numbers.
Whakamārama
Whakamārama, or explanation, used a series of steps to illustrate how something came to be. These were predominantly used when mathematics was employed to answer problems. Therefore, from our initial data set, as well as narratives about how to turn a net into a three-dimensional shape, multistep equations were classified as whakamārama. Other researchers describe this genre as procedural (Wallace & Ellerton, 2004). However, procedures have a sense of involving a lockstep process. For example, from earlier research on genres, Unsworth (2001) described the stages in a procedural text as goal, materials and steps (p. 123). The pieces of writing that we identified as whakamārama certainly explained how something had been done but did not always provide the steps in a set order. An example of such a piece of writing can be seen in Figure 5.
Figure 4 ECAwL4 showing an explanation provided in a nonlockstep manner
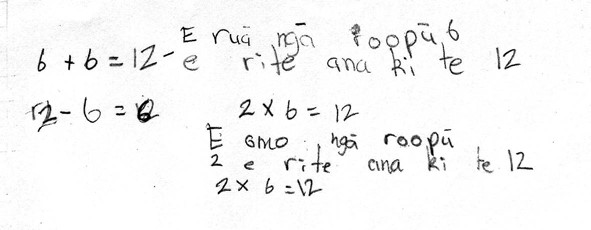

It was often the task that the student was responding to that determined whether a student provided an explanation in steps or in a nonlockstep manner. Figure 5 was a task where students were asked to explain the relationship between addition, subtraction and multiplication. The explanation begins with two related addition and subtraction equations written in symbols on the left-hand side of the page. The related multiplication equation is also written in symbols but underneath sentences state the multiplication in words. The explanation is not described explicitly, but the reader’s eye movement is channelled from 6 + 6 = 12 to 12 – 6 = 6 as 2 x 6 = 12 and on to 6 x 2 = 12. This is because readers of Western languages are taught to seek new information either below or to the left when reading texts. All the equations are related but it is up to the reader to draw this inference.
Parahau
Over the course of the project, far fewer parahau, or justifications, were collected. These were pieces of writing whose primary purpose was to provide information about why something was done. These pieces of writing were more reflective as students had to evaluate what options there were and to discuss why they chose a particular one to use.
Final genres and modes
Although the three basic genres did not change, the number of modes increased as more writing samples were collected. The final collection is given in the list below.

All genres included a range of different modes. However, whakamārama and parahau were more likely to use a combination of modes in the one piece of writing. In the samples that we collected, there were very few justifications that did not use a combination of diagrams, words and/or symbols. In the junior classes where justifications were just beginning to be taught, sometimes these were just narratives. More often, explanations and justifications contained a combination of modes as can be seen in Figure 6. In Chapters 4 and 5, more details are provided on the modes, both individually and how they were combined together.
Figure 5 JCUn
The relationship between field, tenor and mode, and the three genre types
It was quite clear that there was a relationship between the type of genre and the mode that was used. At the meeting in March 2007, the teachers also discussed how different audiences would have an impact on the writing. They felt that sometimes the writing would be exclusively for the student and therefore may convey limited, if any, meaning to others. This would be because of what Wallace and Ellerton (2004) described as “semantic discontinuity” whereby the reader must fill in gaps between the evidence and the conclusions described in order to make sense of what has been written.
Other researchers have connected the explicitness of a piece of communication, either written or spoken, with explicitness of the language used. In 1989, James Paul Gee wrote an article in which he contrasted different perceptions of orality and literacy. He believed that the claims for superiority in cognitive ability connected to literacy were in fact ways to privilege one group’s ways of thinking and thus were tests of participants’ ability to use language in particular ways. He equated this language use with explicitness:
Explicitness in language use can be placed on a continuum between two poles that we might label, following Givon (1970), ‘the pragmatic mode’ and ‘the syntactic mode’. At the syntactic-mode end of the continuum, speakers encode what they want to say using precise and varied lexical items and explicit syntactic structures (e.g., subordinating devices), leaving as little as possible to be signalled by prosody or inferred by the listener. The grammar takes on most of the burden for communication, and social interaction is downplayed. At the pragmatic-mode end of the continuum, speakers chain strings of clauses together fairly loosely through adjunction or coordination, use prosodic devices to signal meaning, and rely on the hearer to draw inferences on the basis of mutual knowledge. Social interaction and the participation of the hearer in a mutual negotiation of meaning are paramount. (p. 50)
Gee went on to link the distinctions based on explicitness to the differences that others had seen as those between oral and written language. What we found in classifying the pieces of writing into genres (and this is described in more detail in Chapter 5) is that all genres contained pieces of mathematical writing that require the reader to provide little or lots of details in order to follow the reasoning. Figure 5 was an example where the reader is expected to draw the appropriate inference. After investigating students’ classroom talk, Barnes (1976) distinguished between exploratory talk and final draft talk. The first type of talk occurs when students are thinking through what they are doing whereas the second is when there is a distant, more formal audience. One of the characteristics that he gave for exploratory talk was that of a low level of explicitness. It may be that writing for self or for an audience is also connected to whether the writing is to help thinking and thus is exploratory or whether it is for publication and therefore is final draft writing.
Predominantly, the teachers at the kura felt that most writing done in mathematics classes was done for the teacher so that they could assess the students’ learning. Similarly, students’ writing in external exams would be for examiners whom they would never meet. On occasions, pieces of writing might also be produced that could be displayed for other students. It may also be that some mathematical writing would be produced to be shown to parents or community members. They would all seem to be likely candidates for the written equivalent of final draft talk and therefore be very explicit as they are written for external audiences. Students’ beliefs about whom they were writing for is discussed in Chapter 7.
The pieces of writing that we collected and then classified into genres suggest that explicitness was less to do with being exploratory or writing for publication, but rather to do with background knowledge of the audience and whether or not one of the primary purposes of the writing was to fulfil an assessment requirement. When the audience had little or no knowledge of the mathematical activity being discussed, such as when the audience was family members, then more explicitness was needed. When the audience needed to know what the student is capable of, there was also a great need for the student to be explicit. Some students struggle with understanding the needs of an audience and being able to respond appropriately (Meaney, 2002a). If the audience for the writing—for example, the writer themselves or the teacher—had been involved in the mathematical task and the recording had no further use once the task had been completed, then the piece of writing was much less likely to be explicit. Therefore, there is a relationship between the explicitness embedded within a piece of writing through the grammatical structures or organisation of the diagrams and the audience. However, this relationship is not simple and relates to the context of situation in which the piece of writing was developed and the needs of the audience.
Given that the genre reflected the purpose for writing, it could be described as the reflection of the field of the context of situation. However, it was also common to find that there were particular audiences and modes that accompanied the fields for particular genres. Figure 7 is one representation of how this relationship could be perceived.
Figure 6 The context of situation for the use of the three genres of mathematical writing
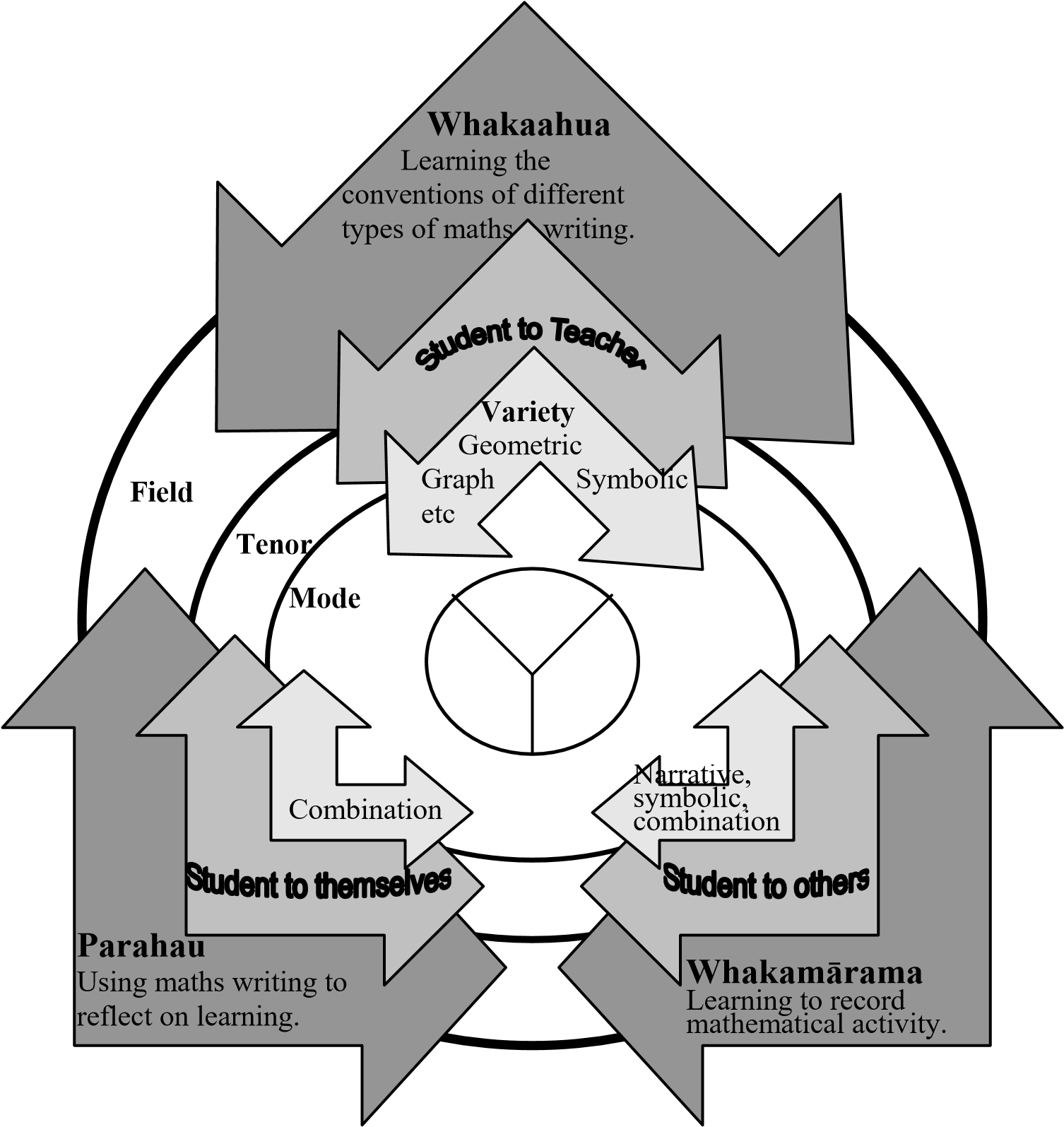
Whakaahua are used to describe mathematical objects or facts. Complexity in these descriptions occurs with the amount of detail provided. Learning to write whakaahua meant that students were also involved in learning about mathematical writing conventions. At the very beginning levels of school, this involves just learning how to form the numbers or shapes. At later stages, students learn the appropriate way to write a number sentence or produce a graph (this is discussed in greater detail in Chapters 4 and 6). Whakaahua fit into what Unsworth (2001) described as “recognition literacy” in that it supports the “learning to recognize and produce the verbal, visual and electronic codes that are used to construct and communicate meaning” (p. 14). Without this literacy knowledge, whakamārama and parahau cannot be produced. However, where Figure 7 is different from the ideas of Unsworth is that he links recognition literacy to common experiences of everyday life whereas in the mathematics classroom, descriptions are very much about moving students into using the mathematics register. Whakamārama is about explaining a mathematical event or phenomenon; thus it is about using mathematics and recording what is done. Parahau, on the other hand, is about explaining why something has been done in a particular manner. This involves participating in reflection about what was done and why. Consequently, writing becomes part of the learning process in a much more conscious way than it is with whakaahua and whakamārama.
Figure 7 DGTrReUnL6

The model in Figure 7 should not be seen as rigid. It will not be the case that the field, tenor and mode are always combined in this way for each of the genres. Of the different parts of the model, the connections to the genres of the different tenor situations are the most contentious. Whakaahua and parahau are not always written by students for themselves or the teacher but can be written for others. For example, Figure 8 provides an example of a description that was written for public display. Nevertheless, it did seem that in our writing samples, whakaahua were mostly produced for the teacher as part of the learning about the conventions of mathematics writing, while whakamārama were mostly produced so that others, including the teacher, could follow the logic of what the student had done. Parahau, even when produced to fulfil the requirements of the teacher, would force a student to do some self-reflection. Therefore, Figure 4 should be considered as one interpretation of the relationship between field, tenor and mode of writing done in mathematics classrooms. It is, however, better to be considered a common combination, rather than the only interpretation of how the field, tenor and mode are related in each genre.
Teacher discussion about another genre
The students’ pieces of writing were all classified using the three genres described above. However, in the staff meeting held on 5 November 2007, there was a discussion about how to include students’ copying of the learning intentions for each lesson. Learning intentions are the teacher’s brief descriptions of what the students are expected to learn in a lesson or series of lessons. Some teachers had students write the learning intentions into their mathematics books. It was unclear how these learning intentions should be classified. There was, therefore, some discussion about whether another genre should be added to the classification:
They are all involved in the activity in some way. They are [providing] either a written representation of the activity which is sort of like the description or they are explaining what they are doing and then some of the seniors get to the point of justifying what they are doing . . . but everything happens within the activity. This sort of stuff happens before or after the activity doesn’t it? You’re setting [the goals for the activity] and the kids are involved in writing so they’re setting or reading with you . . . they are setting the parameters of what they are going to do. Then they are making some judgment about where they are afterward because I think maybe in this writing thing you need to put another category that’s in place for that sort of language. Because they will be using mathematical language whilst not exactly saying what they are doing. (T9, Meeting 5 November 2007)
One teacher (T1) also suggested that students could write the learning intentions in their own words rather than just copying what the teacher had written.
The project ended before this suggestion was followed up, but with research continuing in 2008 it will be interesting to see how this fourth genre is made use of.
Conclusion
One of the primary aims of the She’ll be Write! project was to document the types of writing that were undertaken by students at the kura. Previous research in this area had used genres from other subject areas and there had been little agreement about what would be typical in mathematics classrooms. The teachers at this kura decided to categorise the writing samples according to the functions that they fulfilled. Consequently, three mathematical genres were identified. These genres were whakaahua, whakamārama and parahau, and fulfilled the functions of describing, explaining and justifying.
Each genre was also considered in relationship to its possible main audience and to the modes used to convey the mathematical meanings. The modes used specific types of mathematical writing such as graphs, symbols and narratives. The relationship between the genres, the modes and their audiences is illustrated in Figure 7. The teachers appeared to use whakaahua to teach students about the conventions of mathematical writing. Whakamārama and parahau often used a combination of modes to express their meaning. These genres were related to supporting students to think mathematically and to reflect on this thinking.
3. Whakaahua (describing)
In Chapter 3, the genres and the different modes were described. It showed that ngā whakaahua, or descriptions, commonly only used one mode of mathematical writing whereas whakamārama (explanation) and parahau (justification) often combined a number of modes together. Our data suggest that it is necessary for students to master the different modes for descriptions, before they can use them in whakamārama or parahau.
Ernest (2007) described the conventions of mathematical writing as:
the rhetorical norms that tidy texts into modes of public address. These norms concern how mathematical texts must be written, styled, structured and presented in order to serve a social function, namely to persuade the intended audience that they represent the knowledge of the writer. (p. 66)
Certainly, the data supported the idea that students learn the conventions of mathematical language while learning to write descriptions. However, the pieces of writing in the whakamārama and parahau categories suggest that having control of the writing conventions supports students in their mathematical problem solving. We would suggest that even in the private workings of the messy texts of doing mathematics (Ernest, 2007), it is valuable to have control of the conventions so that students can make a choice over when to make use of them or everyday language in their problem-solving writing. As Meaney (2005a) showed, mathematicians fluctuate between formal mathematical writing conventions and everyday language in their joint problem-solving interactions. The data set included both messy and tidy texts. For us, having students produce whakaahua is a very important part of the process of learning to write mathematics.
Therefore, this chapter looks at how different layers of meaning are added to the modes of mathematically descriptive writing. It seems that adding different layers of meaning is often closely linked to learning different conventions of mathematical writing. Moving students to having control of the conventions of mathematical writing has been studied by a number of researchers. For example, Chapman (1997) was concerned with how students acquired more mathematical language through the interventions of the mathematics teacher. Student expressions such as “it was the same” were rephrased by the teacher as “the difference pattern is constant” (p. 161). Herbel-Eisenmann (2002) discussed the ways that students moved between contextual language, bridging language and official mathematical language. Her contention was that in order for students to be able to join the mathematical community they would need to be able to use official mathematical language. She stated: “‘Bridging’ helps students move from less to more mathematical language by encouraging multiple ways of talking about ideas” (p. 101). However, both these researchers were looking at spoken mathematical language. Although related, the issues surrounding written mathematical language are different and in need of investigation.
It is this relationship between the layering of meaning and the conventions of mathematical language that is explored in this chapter. Our focus is on the development of the modes and so refers very little to the tenor and only occasionally to the field. The field is important because the topic that is being covered has a direct impact on what mode is focused upon. Chapter 5 considers issues of quality of writing in regard to whakamārama and parahau. As later chapters draw on examples of transformational geometry and probability, this chapter mostly uses examples drawn from the modes—graphs, iconic diagrams, narratives, patterns, symbols, tallies and combinations.
In the 2005–6 TLRI project, one of the outcomes was the need to develop an across-the-school understanding about how topics and their accompanying mathematical language developed. There was little information about this for English-medium classrooms and there had been no research on this in regard to the development of mathematical writing in te reo Māori, except what was done in the previous TLRI project. As was noted in the last report (Meaney et al., 2007), triangles had been an area in which the teachers had begun to develop a progression showing how the ideas developed during the time the students were at the kura. It was felt that it would be useful if progressions for other areas were also developed. In the meeting in August 2006 on the possibilities for this new project, the following was noted:
Standards – at year groups
Language of triangles (this year’s project):
– who is responsible for teaching what language?
– when (at what year level) do they need to learn or know particular things?
– what language should be used at what year level?
– stick with simple constructions until such a time as they are ready for more complicated vocabulary? (when will that time be??)
Benefit for the young children if there is consistency throughout:
– learning new vocabulary
– able to condense
– foundation of words—database
– issue—even at year one—there is a limited amount of language to use (known language)
Suggestion of a word bank (familiar words)
– build on what is used at each year level
Writing formalises the mathematical terms and language used:
– same language throughout (consistency)
– consistency of language throughout the school and use by the teachers
– use of language as core content. (Meeting 30 August 2006)
In June 2007, the Tau (Year) 6 teacher, T7, restated this need in a discussion about his aims for the following two terms. He was an art teacher by training but was very reflective about his teaching of mathematics. He stated that his needs at that time were to know what his students would be doing in Tau 7 and beyond so that he knew better what they needed to learn in Tau 6. In the September 2007 meeting he again reiterated the need to know at what year levels different language should be introduced.
Another issue that was pertinent to other kura as well was that many teachers had not been taught mathematics in te reo Māori. This meant that they had to learn the vocabulary and grammatical structures of the mathematics register just before or at the same time as they were teaching it. The following extract from the staff meeting at the end of 2007 illustrates this difficulty for the teachers. The teacher had already discussed in her interview how she had started teaching the concepts of clockwise and anticlockwise turns, only to find that she was uncertain about the terminology to use. As T9 was walking past at the time, she had then asked him about the terms she should be using. In the final staff meeting, she again raised the issue:
For my own planning I need to be aware. You plan your unit but with all the reo that’s involved you can’t just go and copy everything . . . I chased my tail for my āhuahanga [transformation shape] unit. Because I came to you [T9] asking how to do the rotation. When I came upon it, I didn’t know how to say to them, clockwise, anticlockwise, and all that. So I should have had that at the beginning. If I had that structure, instead of running out of the classroom when I saw you coming past . . . So my classroom practice would mean me being a bit more onto it and going through things and knowing how to say this and this and having [it] ready, and since we are all doing the same kaupapa we should all be using them. Perhaps we could do it together—a bit more team planning. (T1, Meeting 5 November 2007)
Part of the reason for collecting writing samples was so that we could provide an overview across the kura that showed the development of the mathematics register. To some degree we did do this, but there is more work to be done and we found out other unexpected ideas while doing this exploration. This chapter provides details both of what we did find and what still needs to be discovered.
By examining students’ pieces of writing, we were able to produce both topic progressions and year-level progressions. Investigation of these writing samples was part of the second tier of research model proposed by Doerr and Chandler-Olcott (in press) that was described in Chapter 2. As had been the case in Chapter 3, it was a second-tier investigation because it was students’ pieces of writing that were being examined by teachers. Appendix A provides an overview of the progressions for some of the modes for descriptions. Appendix B provides the year-level progressions across various modes. It is this final set of progressions that could be used by teachers in developing their teaching programmes.
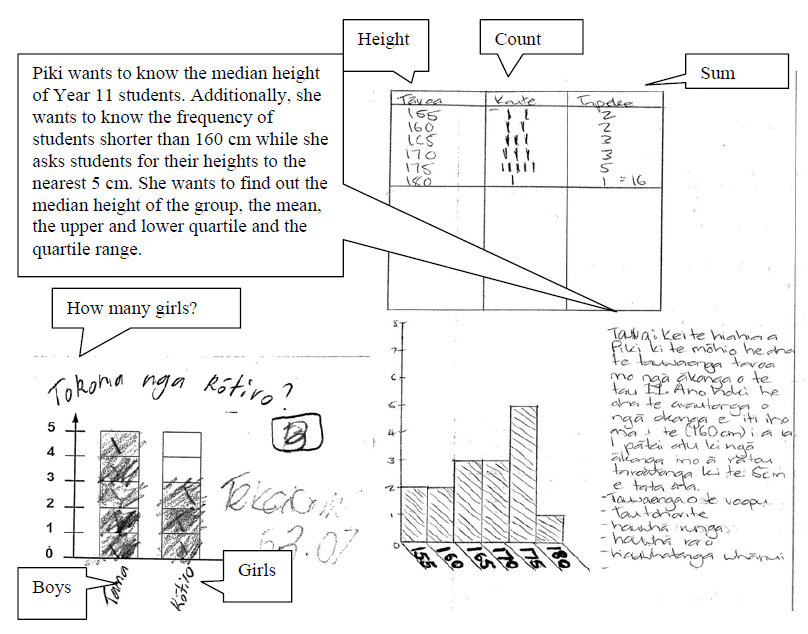
The progressions were built up from looking at the writing samples and identifying their purpose and the primary mode that was used. When more than one mode was carrying the majority of the transmission of information, then the mode was classified as a combination. As with the classifying of the genres, this process was not always simple and compromises were made. Writing of phrases or sentences often accompanied diagrams. In these cases, it was decided to keep the mode as that of the diagram. This was consistent with the classification of modes used by Ben-Chaim et al. (1989) that were described in the previous chapter. It was only when the words provided significantly different information than what was provided in the diagram that the whole piece of writing was classified as a combination. Figure 9 provides an example of two graphs. Although it also has some words and a numeral with it, the first one was classified under graphs, DGrSTeKL3a, while the second one was classified as a combination, DCUnL4. This was because the extra information provided in the sentences in DCUnL4 is new information that is not available from just reading the graph. The extra information provided in DGrSTeKL3a is information that is already given in the graph and so could not be considered new.
Figure 8 DGrSTeKL3a and DCUnL4
Progressions
Once the pieces of writing were categorised according to the genre and then the mode, it was clear that some of the features changed depending upon what was being described. This is consistent with research by Ernest (2007) who described the signs for the semiotic system of school algebra at the lower secondary school level. He outlined what they would look like at earlier year levels as well as at later year levels. Changes, therefore, do occur across the year levels and are well known. However, very little work apart from the geometrical drawing understandings investigated some time ago by Piaget and others (see Piaget & Inhelder, 1956) has been done on what these progressions may look like across a student’s learning of mathematical writing while at school. There are of course other types of mathematical progressions, such as the number knowledge progressions in the New Zealand Numeracy Framework (Ministry of Education, 2007), but these are not specifically to do with the development of mathematical writing.
The topic progressions outlined in Appendix A show how different layers of meaning are added to different modes. An example of these is given in Figure 10 which shows the stages for time. How these progressions relate to school year levels is shown in Appendix B.
Figure 9 The different kaupae (stages) in the progressions of time

Kaupae 1 is seen as the simplest because students are just adding the arms to the clock, whereas kaupae 2 requires the students to draw the complete clock from scratch. There is some sense that the layers are added on top of previous ones, but this is not always the case. Although drawing clock faces from scratch requires students to have more control over the conventions of clock faces, it is quite likely that students would be doing activities around both kaupae 1 and kaupae 2 at the same time. One day they might do one type of activity while the next day they might do the other. Therefore, it is not possible to see these progressions as being linear where one stage must be reached before another stage can be achieved. As with the van Hiele levels of geometric thinking (Nickson, 2000), depending on the activity, students will move between the stages in a fluid motion. Even if they show an understanding of the writing convention at a higher stage in one task, they may return to using the writing style from an earlier stage in responding to another task. A number of different issues, such as who they are writing for and the difficulty of the mathematics involved, will influence the students’ choice.
As was the case with the time progression, often the final kaupae was one that included a written description. In the piece of writing above, the sentences describe activities that are done at the times given on the clocks. A case could be made for categorising this piece of writing as a combination rather than as a time progression. However, as the student had repeated the time in words it was decided to leave it in the time progression. Although these could have been written by much younger children than those who produced the penultimate kaupae, their connection to explanations meant that it seemed more sensible to make them the final kaupae. Sometimes the adjustment of just a few words would have turned a description into an explanation. This was not the case with the example for kaupae 5 of the time progression. However, it was felt for consistency’s sake it would be best to make the final kaupae one that included sentences to support the description.
There were often divisions within the stages. Figure 11 shows the substages within kaupae 2 of the time progression. These are similar to those described by Pengelly (1985) and illustrate the various understandings that the students have to gain in order to successfully draw a clock face.
Figure 10 Divisions within kaupae 2

At kaupae 2a, the student has realised that a clock face is circular and something is written on it. By kaupae 2b, they realise that there is a need for some numbers to go around the outside of the clock face. Kaupae 2c shows that the student has understood that a clock face needs numbers to go all around the outside and that there should be arms on the face. These three substages would all be included in Pengelly’s (1985) first level. She had labelled this as an awareness of the numerals on the clock face. The next stage shows an understanding that the numbers should only go up to 12. This was the equivalent of Pengelly’s second level. It is not until the final kaupae that students are able to place them at appropriate positions on the clock face and also show that the arms are of different lengths. Although not all children would draw clock faces that illustrate each of these substages, it did seem that many children would show at least one of these earlier stages before being able to produce a conventional clock face. However, none of our examples showed the minute marks that Pengelly (1985) had described as the final level.
From looking at the stages and the substages for this progression, it is possible to see the need for students to have control over other aspects of mathematical writing in order to be able to present information about time appropriately. However, this may not correspond with when they gain the mathematical concept to match what they are capable of drawing. In order to be able to draw the arms on a clock, students will need to be able to draw straight lines and determine lengths of lines and the appropriate angles that the lines should be placed at. According to our year-level progressions, at this kura, students draw clock faces from Tau 2, yet drawing of angles is not formally taught until Tau 4 when the terms ä-karaka (clockwise) and huringa tua (anti-clockwise) were introduced with rotation. Actual labelling of angles does not appear until Tau 6. In our database, lines are not a focused area of writing until parallel lines are marked (<<) and labelled at Tau 7. It is possible that measuring the lengths of lines may occur at earlier year levels. However, we collected very few pieces of writing concerning measurement. Even with this limitation, the point is still interesting that students are expected to make distinctions between lines and angles at a stage when these themselves have not been formal areas of study. It would seem that students are expected to be aware of and make use of mathematical writing conventions before these are formal areas of mathematical study.
To draw a clock face, students must have those understandings but also be able to draw circles (if only roughly) and be able to place numbers in order around the circle at appropriate distances apart. Unlike rectangles, squares and triangles, circles never appear as an individual shape on a piece of writing in our database. The writing samples only have circles included as one of several shapes together and thus come under 2D shape progression. Writing numbers in sequential order is also important in drawing clock faces. This is something that is learnt in a similar time frame as that of learning to draw clock faces in Tau 2. However, most numeracy teaching in these early years is around base 10. Clock time uses 12 as its base unit for the hours and 60 as its base unit for the minutes. Although students are expected to draw clock faces at a relatively early age, they are not writing about the distinctions between am and pm time until Tau 5. Students respond to very simple questions involving minutes from Tau 3 but do not respond to complex questions involving understanding 60 minutes in an hour until the intermediate years (Tau 7 and Tau 8).
This would suggest that students are made aware of certain features such as angles and lengths of lines in other situations before they become the focus for a description in their own right. This is reinforced by the fact that shapes such as rectangles, squares and triangles also require an awareness of angle size and line length and are introduced from the first year at school.
The exception is that sequencing of number, that also occurs in clock faces, is a focus for descriptions at about the same time. This may be because of the pre-eminence given to mastery of symbolism in mathematics teaching because ultimately mathematical understanding tends to be associated with being able to provide a symbolic description. Therefore, whenever a possibility arose, the use of symbols was reinforced. O’Halloran (2000) suggested that:
the mathematical symbolism contains a complete description of the pattern of the relationship between entities, the visual display connects our physiological perceptions to this reality, and the linguistic discourse functions to provide contextual information for the situation described symbolically and visually. The major reason why mathematical symbolism is generally accorded the highest status by mathematicians is because this is the semiotic through which the solutions to problems are derived. In this respect, the visual display is not only limited in functionality, but also graphs and diagrams are usually only partial descriptions of the complete description encoded in the mathematical symbolic statements. (p. 363)
The sequencing in the progressions was determined from examining the writing samples. The number of samples that fell into each subcategory varied from one to more than 50. For example, in the time progression there is only one sample of kaupae 2a. However, there are 21 samples from kaupae 4b, from three different worksheets done by students in Tau 7 as part of a unit on time. The largest number of pieces of writing in one substage was 61, in narrative progression kaupae 3a. These samples are one-word or short-phrase answers to mathematical questions and came in response to many different worksheets, tasks or questions. Figure 12 provides some examples of these.
Figure 11 Pieces of writing that were classified as narrative kaupae 3a
 |
 |
 |
Grouping stages across topic progressions
In Appendix A it can be seen that some large topics had progressions that are similar across several mathematical writing modes. For example, angles, lines, 2D shapes, rectangle, square, triangle, 3D shapes, rectangular prism, square pyramid, tetrahedra and triangular prism all seem to have the same set of stages in their progressions. There are also similarities in how symbol representations are developed. Whole numbers, fractions, decimals, integers and algebra seem to have a similar set of stages, although not quite as clearly the same as they are with the geometry modes. Table 3 provides an example of a table showing similarities in progressions. It shows the relationship between iconic and symbolic patterns.
Although the stages seem to be similar for both iconic and symbolic patterns, it would be rare for the stages of both types of patterns to be taught at the same year level. The stages for iconic patterns would be learnt at earlier ages than those for symbolic patterns. It may be that having students become used to the writing conventions of iconic patterns means that it is easier to introduce the writing conventions for symbolic patterns. Although examples are only given for either iconic or symbolic for the final two stages, this should not be taken as a distinction between the two patterns. It is more likely to be related to the collection of writing samples as it is easy to conceive that an algebraic equation could be connected to an iconic pattern and a word description connected to an iconic pattern.
Table 2 Patterns progressions
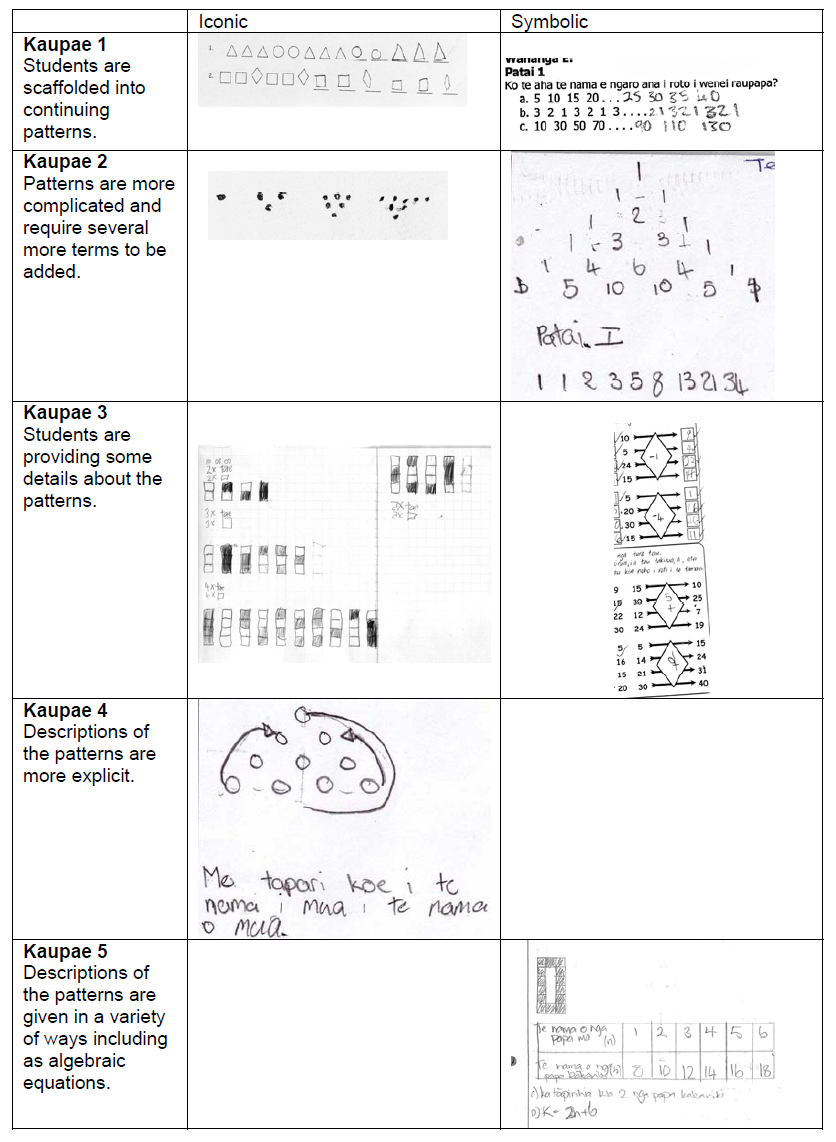
Year-level progressions
The year-level progressions were developed by the teachers. Once the stages of each of the topic progressions were stabilised, examples from each of the stages were provided so that teachers could place them on year-level charts. This was mostly done in the September and October staff meetings. During the principal researcher’s November visit, the year-level progressions were placed on a wall in the staff room and teachers were asked to place remaining samples from stages onto the chart and draw arrows to indicate when they would stop being used. They were also asked to check what had already been included.
Initially, in the September meeting, the teachers worked in three groups to determine which year level they thought that each geometric piece of writing should be focused on. At this time the geometric topic progressions were the most complete and extensive because of the kura’s focus on geometry for the project. The teachers were asked to think about where the ideas should be first taught and at what year level students would stop using them. They were to discuss in their groups where they felt the samples from each stage should go. The samples were then stuck on to a large chart under what they considered to be the most appropriate year level. At this stage, groups of teachers could have placed the same idea at different year levels. If this occurred all the teachers discussed together what they believed was the most appropriate year level or whether the writing began at one level but was revisited for several years.
After the initial placement of the writing samples, the teachers for each year level considered what the kura was expecting them to teach and decided whether they agreed with this. A considerable amount of discussion occurred among the teachers about the most appropriate years for the writing to be taught.
Findings from the year-level progressions
Examining the year-level progressions produces a number of interesting findings. Firstly it shows that the stages in the topic progressions are not linear, as discussed in the previous section. Usually, later stages are introduced at later year levels but this is not always the case and it is these exceptions that indicate that it is not a linear progression. Secondly, an examination shows that a related series of stages across modes would not always be introduced at the same year level. For example, being able to draw iconic patterns begins at Tau 1 while being able to produce symbolic patterns does not occur until Tau 3.
However, other findings also became evident with the year-level progressions acting like a fossil record of mathematical writing. This is not to say that stages record extinct remains but rather that there is a variation in how mathematical writing conventions develop. As a fossil record, what they do show is when mathematical writing conventions are introduced and when they are no longer used in mathematics classrooms. The reasons for the occurrence and disappearance of various stages of the modes are varied. One reason is due to the database being incomplete. However, it is also clear that there is a range of other reasons why a particular stage of a mode disappears. These are discussed in the following paragraphs.
Some mathematical writing conventions, such as tallies, are introduced in the first years of kura and remain unchanged at later year levels. DCUnL4 in Figure 9 shows a tally that was used by a student in Tau 11. This is not dissimilar to the tally used by a Tau 1 student (DSWNMaL2a) or one used by the teacher to keep class points that can be seen in Figure 13.
Figure 12 DSWNMaL2a (left) and classroom points tally (right)

Another reason for the disappearance of stages of modes in topic progressions is because writing conventions are transformed and appear at other stages. For example, once students master clock faces (kaupae 2) in the junior years of the primary school, they are not drawn again in later years. Instead, simplified versions are incorporated into summaries of different versions of giving time (kaupae 3) and from Tau 8 are not used even in this simplified form. This shows clearly that the recording of time information has been transformed into other forms, most commonly numerical either in 12- or 24-hour time. Time itself also stops being a focus of explicit teaching from the junior high school years because it is expected that students have mastered being able to solve problems involving time (kaupae 4) by this stage.
Similar examples can be found in other topic progressions. Kaupae 1a of the symbolic—whole number progression—involves students tracing numbers. Examples of this type of writing were drawn only by students in Tau 0 to 2. Kaupae 1b involves the students drawing an appropriate amount of objects to match the numeral that is given. This would only be expected of students in Tau 0 to 1. At the same time students were also expected to independently produce numerals. The information that is attached to these numerals becomes more complex as students move through the substages of kaupae 2. Table 4 shows each of the substages and provides information about the year levels that they occur in.
Table 3 Substages for whole number kaupae 2 progressions

Each substage provides an extra layer of meaning about numerals and how they can be used. At kaupae 2e, the numerals are still recognisable as being the same as those produced at kaupae 2a, even though they now have more than one digit. However, the descriptions that they provide are very different at each of the substages. Numerals do not disappear over the years of schooling nor are layers of meaning lost by moving through the substages. Rather, it should be considered that the numerals accumulate layers of meaning as students progress through their schooling. Not all of the layers may be actively used by a student when doing mathematics but they are available if needed. Therefore, the various substages and stages of different topic progressions can appear and disappear over the year levels.
As well, some progressions disappear altogether from the year levels because their purpose was to introduce another progression. Iconic pattern progressions become extinct or at least appear less frequently in the high school years. As their primary function may have been to introduce symbolic patterns, once students are competently using them the purpose of drawing patterns becomes redundant. This may be why this progression disappears from the year-level progressions. Iconic pattern progressions, therefore, could be seen as examples of what Herbel-Eisenmann (2002) called “bridging” language. It enables students to talk about patterns whose features are visually more noticeable than those of many symbolic patterns. In this way, students gain ways of describing patterns in writing that then can be transferred to when they describe symbolic patterns.
One of the aims of working with patterns is to be able to provide algebraic equations to describe various patterns, but in order to be able to do this students need to understand the distinct features of patterns. This is done through using writing to focus on small numbers of these features at one time. The various stages of the progressions show the change in focus on the features. Introducing this focusing process by first working with iconic patterns can be thought of as a way of easing students into understanding the importance of these features.
Much harder to understand is the appearance of short-lived progressions that do not seem to be related to other mathematical writing convention progressions. The progression that we have labelled as Technical Drawing would be one example of these. This progression has only two stages, examples of which are given in Figure 14. Both appear (at Tau 7) and disappear (at Tau 11) at the same time.
Figure 13 DGTDRaL1 (left) and DGTDMaL2 (right)
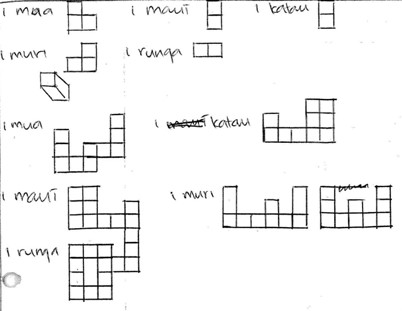 |
 |
It would seem that they have a short life and connect with nothing else. Although they could be related to perspective drawings of 3D shapes such as rectangular prisms, the pieces of writing that we have do not make such a connection. It is, therefore, unclear why students are expected to learn these mathematical writing conventions.
It may be that it involves students in visualisation that is necessary in other fields of mathematical learning. However, there appears to be some contention about whether focused teaching increases spatial visualisation skills (Ben-Chaim, Lappan, & Houang, 1985). Being able to draw different faces of an irregular 3D shape and to represent it on isometric paper from other 2D representations of these objects requires students to be able to produce and manipulate mental images (Ben-Chaim et al., 1985). Being able to visualise flat, 2D images as having the depth of a 3D object requires students to learn how to make use of the conventions of the depth cues in the representations (Lowrie, 2002). These are Western conventions that take time for students to develop and involve considerable interaction with real-life objects (BenChaim et al., 1985). By the time students reach intermediate school level, it could be assumed that students would have had this interaction and could then take advantage of writing lessons that specifically focused on drawing 3D shapes on paper. The ability to produce mental images becomes essential in working with many mathematical ideas in high school. Like learning about time, it may also have some relevance to being able to deal with outside-school mathematical problems. Being able to read architectural plans is not something that is formally taught in schools but is something that many adults at one time or other have to be able to do. However, the connections are not clear and it may be difficult for some students to understand the point of learning these skills.
Conclusion
The development of progressions was done so that the teachers had an understanding across the kura of how the language attached to mathematical ideas developed. The stages in the topic progressions provide details of how layers of meaning are attached to the different modes. The substages show some of the features of each stage are developed so that students become proficient in describing the particular layer of meaning of the stage. Examples were provided from the time progression to illustrate these points. The similarities between stages of iconic and symbolic patterns illustrated how related modes could also have the same development of layers of meaning. This was not always the case because the three types of graphs each had very different progressions.
The development of the year-level progressions was done by the teachers after discussion with each other. These progressions will be of use to teachers in their planning. However, they also provided information about the topic progressions. For example, they reinforced that the topic progressions should not be considered as linear and that the stages of related progressions are rarely introduced in the same year level. By considering the year-level progressions as a fossil record, it was also possible to understand why some progressions appeared and disappeared at different year levels. Tallies, for example, could be considered as tuatara in that they appeared in the earliest years of school and were still appearing in the same form at the end of high school. Other progressions appeared for a few years but then transformed into other modes of mathematical writing. For example, iconic patterns disappear and are replaced by symbolic patterns, although there are a few years where examples of each would be written. The third type of “fossil” would be those like technical drawing that make a fleeting appearance in the year progressions but do not appear to be related to other progressions either before or after their appearance.
4. Whakamārama (explaining) and parahau (justifying)
Learning how to write whakaahua involved learning the conventions of mathematical modes and this was described in the previous chapter. This chapter looks at how these mathematical writing conventions are integrated in explanations and justifications. Students’ explanations and justifications have received attention by researchers because of their potential to improve the students’ learning of mathematics (see Forman, Larreamendy-Joerns, Stein, & Browns, 1998). The definitions that the teachers had given to whakamārama and parahau were:
| whakamārama (explanation) | Explain the process | How do you get there? | |
| parahau (justification) | Justify the result | Why is this best? |
These have similarities with the definitions given by others. Bicknell (1999), using the work of Thomas (1973), suggested:
[a]n explanation can be defined as making clear or telling why a state of affairs or an occurrence exists or happens, whereas a justification provides grounds, evidence or reasons to convince others (or persuade ourselves) that a claim or assertion is true. (p. 76).
Another who has done research on students’ explanations and justifications is Erna Yackel (2001) who, using a symbolic interaction perspective, stated that :
[s]tudents and the teacher give mathematical explanations to clarify aspects of their mathematical thinking that they think might not be readily apparent to others. They give mathematical justifications in response to challenges to apparent violations of normative mathematical activity. (page ref)
All these definitions suggest that whakamārama and parahau are both kinds of mathematical arguments. In regard to solving problems, Meaney (2007) wrote “[a] convincing argument makes a clear connection, using reasoning, between what is known about a problem and the suggested solution” (p. 683). Thus, both whakamārama and parahau are providing mathematical arguments because they outline their reasoning for solving problems, although their focuses are different. From analysing discussion in mathematics classrooms, Krummheuer (1995), using ideas from Toulmin (1969), proposed four components of argumentation: claims; grounds; warrants; and backings. These are outlined in Figure 15.
Claims are assertions of a point of view; in most cases these are the proposed solutions. Grounds are the unchallengeable facts from which the assertions are drawn. Warrants are the pieces of information which join the grounds to the claims, while backings provide the contexts for when the warrants are appropriate. A difference between whakamārama and parahau could be the inclusion of warrants and backings. An explanation would provide some warrants as they show the steps that the writer has gone through to reach their solutions. However, a justification would also need to provide the backings for why the warrants are valid.
Figure 14 Diagram showing the relationship between the components of an argument (adapted from Krummheuer, 1995, p. 245)
Benefits of writing
Both whakamārama and parahau were seen by the teachers in this project as being very valuable for students learning mathematics. In the June 2007 staff meeting, teachers played a place value game that was similar to a game that many of the teachers played with their own students. The game provided a focus for discussions about how to gain the most benefit from having students engage in mathematical activities. The teachers had to write down their strategy for winning and their reasons for why they felt the strategy worked before they played the game again. They could then modify their strategy. Following on from this activity, the teachers had a discussion based around the following questions:
- What benefits do you see for children in answering questions about their strategy use?
- What benefits do you see for teachers in having children answer questions about their strategy use?
- Are there any other benefits in having children write their answers rather than speak them?
The following is a summary of this discussion taken from the meeting notes (6 June 2007):
Benefits for children
- In junior classes, writing about what they are doing in mathematics gets children familiar with having to write about their thinking. Having children write about a strategy rather than just play the game means that some of them become aware that a strategy is required in order to win the game. Although teachers implement games because they can see the mathematical learning that is possible, children may think that it is just luck that helps them win. Making children explicitly aware of their own and others’ strategies can mean that the mathematical learning opportunities are made more accessible to the students.
- The process of having children write about their strategies in mathematics means that children cannot hide but must meet the expectation that they will have a strategy. Having students write about how they got their answers promotes metacognitive evaluation of what they did. They can use these reflections to refine their strategies and increase their learning opportunities. By writing about their strategy, children will have more time to reflect on what they did and why.
Benefits for the teacher
- Having children write about their strategies means that teachers become aware very quickly of who does not have a strategy. This may not always be possible when the strategies are discussed orally.
- Being able to explain and justify their answers requires students to be able to both do the mathematics and also to use the appropriate linguistic resources. Teachers can determine from students’ writing and their participation in the activity whether it is the mathematics or the language that causes students’ problems.
Specific benefits of writing
- Concentrating on writing means that the question can be asked: What do you want to do with language, rather than just maths language?
- Writing enables an activity to be spread over time as the results can be referred to again and again. This is not possible when an oral discussion occurs. Poutama Tau encourages students to talk through their responses. This can be built on so that there is explicit teaching about writing genres. The teacher models answers and strategies. Children can write to express what they are doing and this can be developed into explicit writing of different genres. By having students write about what they have been doing, they can consolidate their learning. Quiet children who may not have participated in a discussion will be encouraged to have a strategy. However, it is recognised that there is a relationship between speaking and writing. Children are more likely to write well if they have had opportunities to talk about what they are doing. This leads to the question of how to ensure that every child has an opportunity to talk about what they are doing.
- It is useful in later years if children have got used to writing in the junior classes.
- Children can be encouraged not just to answer problems, but also to write their own problems.
From this discussion it can be seen that the teachers felt that having students explain their reasoning through writing explanations and justification was important, even though this is not explicitly mentioned. This supports what other researchers have suggested. For example, Moskal and Magone (2000) stated that “students’ written explanations to well-designed tasks can provide robust accounts of their mathematical reasoning” (p. 313) and so can be used by teachers to assess students’ knowledge. However, there is a need for teachers to expect students to use these genres as well as supporting students to produce them. It is only within the social milieu of the mathematics classrooms that students will be channelled into responding to these expectations. As Yackel (2001) wrote, “the understanding that students are expected to explain their solution is a social norm, whereas the understanding of what counts as an acceptable mathematical explanation is a sociomathematical norm” (p. 14).
Although we had collected some samples of explanations and justifications from the senior classes before this June meeting, it was clear that other teachers took up the challenge of expecting students to write whakamārama and to a lesser degree parahau during the final two terms.
However, having students write whakamārama and parahau was something that teachers were still grappling with over the course of the whole project. By the November 2007 staff meeting, some teachers, such as T7 and T3, were able to describe the strategies they had recently adopted for having their students write explanations and justifications. For other teachers this was still something they wanted to work on in 2008 as the fourth term of the year was not seen as being a good time to start something new. This is discussed in more detail in Chapter 8.
Identifying whakamārama and parahau
The next two sections describe the distinctive features of whakamārama and parahau. We used a linguistic analysis approach to identify these features. There are a number of ways that the features could have been identified. Lankshear and Knobel (2004) suggested a range of questions that could be answered when doing a critical linguistic analysis. These were:
What is the subject matter or topic of the text?
Why might the author have written this text?
Who is the intended audience? How do I know?
What kind of person would find this text unproblematic in terms of their values, beliefs, world views, etc.?
What world view and values does the author hold or appear to hold? How do I know?
What knowledge does the reader need to bring to this text in order to understand it?
Who would feel ‘left out’ in this text, but should logically be included? Is this exclusion a problem? Are there important ‘gaps’ or ‘silences’ or over-generalisations in this text? For example, are different groups talked about as though they constitute one homogeneous group?
Does the author write about a group without including their perspectives, values, beliefs in relation to the things or events being reported?
Who would find that the claims made in this text clash with their own world view or experiences? (p. 342)
Our interest was in the ways that students presented their mathematical ideas so not all of Lankshear and Knobel’s (2004) questions were relevant to the analysis that we wanted to do. These questions raised our awareness of the need to consider how students expressed their Māori identities through their mathematical writing. Mathematics is a Western construct that consequently is overlaid with Western assumptions about knowledge in general. This is manifested in the mathematical register that developed concurrently with the development of the mathematical ideas (Meaney, 2005a; Roberts, 1998). Nonetheless, Burton and Morgan (2000) found that it was possible for mathematicians to individualise their writing to reflect something of their personality and beliefs about mathematics. Meaney (2006a) also found that there were differences in how primary school students expressed themselves that were related to age, gender and the decile level of the schools they attended. However, there were also differences in students’ oral responses according to how the task was expressed (Meaney, 2007). Discussions about who the author was writing for and their purposes for writing are discussed in more detail in Chapter 7. An interesting area for further research will be to investigate the linguistic choices that students make as a way of investigating how they express their Māori identities.
The linguistic analysis used ideas around multiple literacies and how different modes are connected to present mathematical ideas. It therefore drew on the ideas of O’Hallohan (2000), Kress and van Leeuwen (2006), Lemke (2000) and Unsworth (2001). All of these researchers used understandings from Halliday’s (1985) systemic functional grammar to discuss mathematical symbolism, images, scientific multiple literacies and other multiple literacies respectively. Although none was directly relevant to the analysis undertaken with the samples we had, they did provide insights into what may be important features. In particular, these researchers highlighted the importance of the positioning of the visual images, the way the main participants (including mathematical objects) are emphasised and how coherence is maintained. For students in Johanning’s (2000) study, drawing pictures, graphs or a table was the first thing they did when they began solving a problem. However, they rarely saw this as a problem-solving strategy, but, rather, as a way of organising information. It was therefore useful to concentrate on explanations and justifications that used combinations of modes. In the discussion of the following kaupae, or stages, these ideas will be discussed in regard to systemic functional grammar’s ideas about field, tenor and mode in relationship to the context of situation in which the pieces of writing were developed.
Whakamārama
The primary purpose of whakamārama was to provide the reasoning for getting a particular answer, usually in such a way that another person would be able to reproduce it or that the author could remember what they had done. Explanations most often used a combination of modes. However, there were also 21 examples of explanations that only used symbols. There were also two pieces of writing that were classified as whakamārama and only used sentences. One of these can be seen in Figure 16.
Figure 15 ENArL3

The samples of whakamārama that were classified as combinations used a range of different modes. Most often they used some symbols and/or some words. However, there was also a large number of explanations that focused on geometrical ideas and thus also contained diagrams of shapes. As other chapters use examples from geometry and probability, in this chapter the examples will be drawn from other topics.
The following sections look at the simplest to the most complex explanations in our database. Differences in complexity are to do with how the different elements are combined to fulfil particular needs. We have not used whether or not the piece of writing was transparent or opaque in its explanation in the way that we determined the stages. This is because we saw the transparency as being related to the audience requirements rather than to the complexity of the writing.
It is not expected that students should be aiming to write the most complex explanation every time and so a simpler explanation should not be considered to be of a lesser quality. A discussion about judging the quality of an explanation or justification comes after the sections on whakamārama and parahau.
Figure 16 ECUnL1
Kaupae 1

I used eighteen 2 times
I worked out 5 lots of 16
I worked out 3 lots of 10 and 3 lots of 4 I worked out 4 lots of 10 and 4 lots of 3
I worked out 2 lots of 19
I worked out 5 lots of 20.
Figure 17 provides an explanation of some multiplications. Single-step multiplications would normally be classified as whakaahua as they just describe a basic fact. However, in this example, the student gives a brief explanation of how they worked out the answers but does not provide the particular strategy they used. Given that the Poutama Tau professional development project suggests that teachers have students explain how they worked out their answer, it is quite likely this is what the teacher had expected the student to provide. Instead, this student has mostly simply stated in words that they multiplied the two numbers together.
1. I whakamahi au i ngā teka[u] mā waru e 2 ngā wā (I used eighteen 2 times)
However, answers 3 and 4 are somewhat different in that they break down the multiplication into two parts: first the tens and then the ones. This shows a two-step process and moves the piece of writing from being classified as whakaahua to whakamārama. There are no warrants that would justify why it is useful to break 14 or 13 into their composite tens and ones.
| 3. I mahi au 3 ngā tekau me 3 ngā 4 | (I worked out 3 lots of 10 and 3 lots of 4) | |
| 4. I mahi au e 4 ngā 10 ara i mahi ara 4 ngā 3 | (I worked out 4 lots of 10 as well as worked out 4 lots of 3) |
Explanations at this level are the simplest because the arrangement of information does not require the reader to integrate different representations simultaneously. Although mathematics should not always be read from left to right (Meaney, 2005a), this is the case for the piece of writing in Figure 17. Each answer is numbered and written down the page, then the multiplication operation with its constituent parts (number, multiplication sign, number) is provided, followed by the main relationship indicator as a process (=) and then the result. Each of these multiplications is then followed by its explanation written mostly in words but also with at least one numeral. The length of the word explanation is shortest for the final two statements and provides a repetition of the symbolic multiplication without any elaboration.
Using a systemic functional grammar approach to analyse the pieces of writing is to look for equivalents of field, tenor and mode of this piece of writing. The field is clearly that of doing simple multiplications on paper and this is recognised by the placement of the equation on the left-hand side of the paper. It was common in our samples to find the main focus of mathematical writing to be on the left with elaborations on the right. Lankshear and Knobel (2004) suggested that items on the left of the page tend to be more salient in terms of attention and importance than items placed on the right. This is because our writing system generally uses a left-to-right movement so that items placed on the left would be considered first.
The tenor of a text is reflected in the use of personal pronouns and the mood of the verb used. The responses in Figure 17 follow closely the symbolic calculations rather than how they would be said out loud in te reo Māori. Thus the mood of the verbs could be said to be “mathematicised” and to have removed a recognition of the author.
On the other hand there are repeated references to the author, au (I), in the second part of the response. The numerical equation, as is typical of mathematics, makes no reference to humans and in so doing represents itself as an unchanging fact (Burton & Morgan, 2000). However, the use of au suggests that this should be considered a personal piece of writing. It was the writer who was working out the answer and was responsible for its accuracy. Yet the clarity of the piece suggests that it may have been written with an expectation that it would be read by someone else or at least would be read by the author again at a later date. A similar example of writing is provided in Figure 18, but in this case the lack of transparency in displaying the meaning makes it unlikely that it was written for someone else to read.
Figure 17 ESUnL1
In the example given in Figure 18, the student is showing that doubling a multiplier gives double the product. Although the way the information is set out in Figure 18 is similar to that in Figure 17, there are fewer words and, from answer 5, making opaque the explanations of how the responses are gained. The reader must look across the page to locate the relevant information. This is much less a tidy text (Ernest, 2007) and is more likely to have been written for the writer than for an external reader, unless the reader has enough background information to fill in the missing links.
The mode of Figure 17 involves using numerical equations followed by sentence explanations. Cohesion is achieved through the repetition of the numbers in the sentences. As well, the pattern of the sentences is similar for all the responses so that visually it clues the reader into not expecting any major differences in the types of explanations.
Figure 18 ECUnL3
Kaupae 2
The words in the middle of Figure 19 state “[f]ind the information for Gauss 1–16 boxes of 4”. The 4 x 4 grid under the word Gauss, at the top, is repeated with grid lines in the bottom left corner. This grid shows how the numbers are arranged so that each column and row adds up to 34, thus providing another method for determining the sum of the numbers. In the top right corner, is a 3 x 3 grid showing how the numbers 3 to 11 can be arranged in columns (or rows) to equal 21. It is a simpler example of using the grids.
In the bottom right corner, eight combinations of 17 are shown by using connecting lines between numbers. Underneath this is “= 136” which is the total sum of the numbers 1 to 16. However, another operation is then connected to 136 by the addition of ÷ 4. The result of this is given as = 34. There is no discussion about how this would be an effective method for addition. If there had been, it would have been classified as a parahau.
The piece of writing in Figure 19 is typical of kaupae 2 as it requires the reader to integrate a variety of different visual arrangements. It uses grids (3 x 3 and 4 x 4), sequences of numbers, connecting lines between numbers and mathematical operations using = and ÷ signs, as well as words. However, it is showing the same process in a number of different ways and thus is not as complicated as a piece of writing that integrates a variety of new information.
How a reader would make sense of pieces of writing at this stage would depend upon their previous understanding. It is not transparent and therefore it is unlikely that it was written for an audience unfamiliar with this topic. Although Gauss’ name is underlined, it is unlikely that someone who did not know Gauss’ strategy would have any entry points into what is being explained. Thirty-four is highlighted by the writer by surrounding it with a box. However, its connection to anything else, except 136 ÷ 4, on the page is not transparent. The sentences do not give sufficient detail to fill in the missing gaps in information.
Using ideas from systemic functional grammar, it is possible to see that the field has something to do with sequential numbers (although their arrangement in the grids does not make this particularly clear). Both the underlining of Gauss’ name and the surrounding of 34 in a box suggest that these are the main participants. The lack of transparency in the explanation suggests strongly that it was written by the author for him/herself or for someone else who was already familiar with Gauss. This lack of transparency can be considered as a way of understanding the tenor of the context of situation. The mode is represented by the use of sequences of numbers, grids containing numbers, connecting lines, mathematical operations and words. Although there is repetition of the numbers, the cohesion of the text is not clear. It is difficult to recognise the new information and how it builds on what was previously provided. In fact it is difficult to know whether the writer even expected the audience to read from top to bottom or from left to right.
Figure 19 ECTeWL3
Kaupae 3

With the problem given at the top of the page, it is clear that Figure 20 provides the workings about this problem. On the left-hand side of the page, going from top to bottom are diagrams representing the coloured blocks. The copying and scanning have removed the colour so the diagrams are not as clear as they might be. However, the first line of diagrams has been disregarded and the second line is the appropriate one. The last line of diagrams shows a more complex set of combinations of blocks. The sentences written on the right-hand side provide an explanation of the pattern. This is the same sort of arrangement as those seen in Figures 17 and 18 where the main focus is on the left side of the page and the written explanation is on the right. However, underneath this pattern is a sequence of numbers 4, 8, 16, 30 written both horizontally and vertically on various places on the page. The additions given in a numbered list also refer to this sequence and appear to continue it further. However, there is not enough detail to know where it comes from and indeed what its relationship is to the list of additions.
The field is one of explaining patterns. This is realised through the inclusion of a visual representation of the first pattern and a repetition of the sequence of numbers forming the second pattern. Repetition appears to be a common way in our mathematical samples to emphasise what is being done, as well as providing cohesion. In this piece of writing, the tenor seems to change halfway through. The clarity of the explanation of the first pattern would suggest that it may have been written for someone else. However, the explanation of the second pattern based on the sequence of numbers is impossible for a reader to follow unless they were present when the activity was undertaken. The mode shows that the student used three different mathematical modes of writing: diagrams; word explanations; and symbolic explanations. Cohesion is achieved by repetition. In the first part it is the drawing of and the writing about pouaka (box). In the second part it is through the repetition of the sequence of numbers. New information appears to the left of or below previous information.
Kaupae 4
Figure 21 is really a series of explanations that are related to simplifying algebraic expressions and equations. These are the bulk of what appears on the page. Each one is separated by a blank space and begins on the left-hand side of the page, except for (10) that is written on the right-hand side of the page. Some algebraic equations are dealt with in one line, whilst others are explained over several lines. They may or may not have accompanying word explanations. As well, there is a general explanation of some of the rules for doing algebraic equations in the right-hand margin. Each equation could be thought of as belonging to a lower stage. However, their close proximity, the addition of repetitive features such as word explanations and arrows, as well as the set of general rules in the left-hand margin, suggest that this should be considered as one explanation. Consequently, it is up to the reader to make sense of all the parts and how they are related. This is what makes this such a complex explanation.
Figure 20 ECMa1L4

Therefore, the field is that of doing algebra, but it is also clear that this student is only at an early stage of learning how to make use of it, hence the inclusion of the arrows and written explanations. The clarity of the explanation suggests that it is for someone else to read or for the author to reread at a later date. With an audience for this writing, there is a need to be clear in providing details. The mode involves the students using algebra and words for providing their explanation. They have also used intermediate or bridging mathematics language (Herbel-Eisenmann, 2002) in their use of arrows to show how the expansion of the brackets is done. Cohesion is achieved through the repetition of the variables, although in different equations. This is one of the aspects that makes it a complex explanation in that there is a need to see both the similarities and the differences in how each equation is solved.
Summary
Whakamārama provide some insight into the students’ thinking as they give the information, or the warrants as described by Krummheuer (1995) that connect the problem with its solution. Explanations that use a combination of mathematical modes are often not simple pieces of writing to read. This is because they do not always set up the connections between the different formats of information clearly. Even at the higher stages of these explanations, it is not always easy to follow the reasoning unless there are word descriptions to accompany the explanations. These word descriptions become even more important in the production of parahau.
Parahau
Writing parahau involves the student justifying their answers. This involves the student providing a backing that contains details for the warrants. Knowing when the warrants are valid and why, would be the information that would convert an explanation to a justification. There were only eight of these in the database. The simplest of these was one written in words as a response to some questions about reflection.
The worksheet shown in Figure 22 required the student to draw both the object and its reflection. By having the heading at the top of the page, followed by the diagrams, it is clear that students are expected to use what they have done to answer the questions in words at the bottom. The questions could be interpreted as asking students to justify the placement of their reflections by mentioning the distance from the mirror line. Instead, the student has concentrated on making sure that the reflection is exactly the same as the original diagram. However, the mention of orite (same) would still provide a backing for the warrant, about using the mirror line as the focus for the reflection.
Figure 21 JCTeA
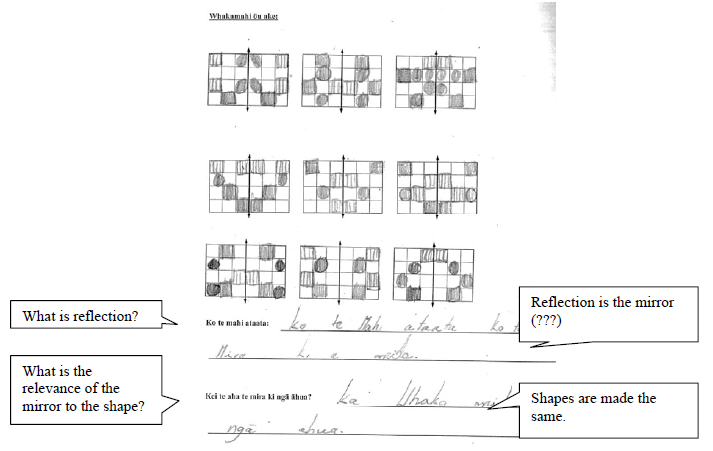
The field for this parahau is that of reflections. This is emphasised by the heading at the top of the page, followed the diagrams and the written questions, all of which repeat the theme of reflection. The tenor of the piece of writing is that of a student responding to a teacher’s request for them to show what they know about reflection, and as such is an assessment piece. The student, therefore, is not only answering questions, but also having to determine what the teacher wants to know from the questions. The student cannot simply respond in any way he or she likes; there are obligations when it is an assessment piece for them to tell to the best of their ability exactly what the teacher wants to know. The mode includes using diagrams and sentences. Cohesion is through the different representations of reflection and the repetition in the different forms enables the focus to be maintained.
The reasoning that is used to justify the way the reflections is done is procedural in that it refers to whether the process is correct rather than if the process is the appropriate one.
Figure 23 provides an example of an implicit justification that is based on reference to a set of mathematical facts. The two images in Figure 23 came from a student’s mathematics book and were on sequential pages. The first image is a description that provides labels for each side of a right-angled triangle. It also provides a visual description of the relationship for the sine, cosine and tangent rules. Below these sets of triangles, are equations given in words that state what the relationship is. In the second image, students are working out the length of the missing side and also the size of the angle. To work out the length the student has used Paitakōrahi (Pythagoras’) rule and to work out the size of the angle, the whenu (cosine) rule. An implicit justification for using the cosine rule is given by the repetition of the triangles showing the different rules from the previous page. This is the backing that supports the warrant for using the cosine rule. It has been written in the left-hand margin of the page. A reader must be able to read this combination. Without specific questions, they need to have appropriate knowledge to follow the explanations for solving the problems and to recognise the triangles on the left-hand side as the implicit justification.
Figure 22 DCUnL2 (left) and JCUn (right)
The field is one of answering questions about right-angle triangles, even when they are dressed up to be questions about a tree. The tenor is most likely to be the writer writing for themselves. The margin notes, as well as serving as a backing, are also a reminder of why a particular approach was taken for when the writer rereads it later. The mode involves a diagram of a tree which has been overlaid with a triangle. The use of the right-angle sign is supposed to indicate a right angle, even though the rough drawing does not suggest this. The drawings of the triangles are different from the right-angle triangle because they serve as information summaries.
A more explicit justification can be seen in Figure 24. This example was drawn as a result of students being challenged by their teacher to produce the dimensions for a cylinder that would hold one litre. The students had to justify what they did. A number of different approaches were taken.
Figure 23 JCKa1
The approach that this student took was to decide that the whitianga (diameter) was 10 cm and thus the pūtoro (radius) was 5 cm. She then determined the area of the circle at the top of the cylinder. Using this area and that one litre is equivalent to 1,000 cm3, she calculated the height of the cylinder. All the calculations are done using symbols, numbers and algebraic variables. The justifications for what was done are provided in sentences or phrases connected to the calculations with lines. Not every decision is provided with a justification, such as why the student began with a diameter of 10 cm. However, the majority of decisions are provided with a reason. Although the calculations proceed from the top to the bottom of the page in a logical order, the addition of justifications disturbs this flow as it requires the reader to follow the lines upwards and downwards as well as sideways. However, as was the case with many of the whakamārama, most of the justifications written in sentences appear on the left-hand side of the page.
The field is that of a student using their mathematical knowledge to solve the problem of working out the dimensions of a cylinder for a specific volume. The key aspects of the calculation are often labelled in the justifications. Whitianga and pūtoro are both labelled in the main part of the writing and pūtoro appears in the equation for the area of a circle as “p” in the following line. Although the piece of writing represents the working notes of the student, the addition of the justification suggests that the teacher will read it and expect the reasons to be made explicit about the decisions that were taken during the solving. The nonlinear addition of the justifications shows that this was not a polished piece of writing that would have a wider audience. The mathematical writing modes were words, sentences, algebraic calculations and a 2D representation of a cylinder. Cohesion is achieved by the repetition of the main participants in the calculations, either as labels or numbers in the calculations. The justifications also made quite explicit what the connection is between these components.
Summary
Justifications are different from explanations because they do not appear as part of “doing mathematics”. Although everyone would have reasons for what they do in mathematics, it is only when they make them explicit with their workings that they would become part of a piece of writing. Their addition to mathematical explanations means that they often appear on the margins (and in the case of Figure 23, literally in the margins) around the explanations. This is especially the case when they are added to workings rather than to a polished piece of writing that could be expected to have a wide audience. It may be possible that a polished piece of writing may find other ways to incorporate the justification, but this did not occur in the samples that we had collected. Generally, justifications are provided through providing words on the right-hand side of the page with the calculations on the left.
Judgements about the quality of mathematical writing
For teachers to improve the quantity and quality of students’ writing, then, there was a need not just to understand the features of explanations and justifications, but also to have a clear understanding of what constituted a “good piece of writing”. Identifying the features of an exceptional versus an average or unacceptable piece of mathematical writing is something that is rarely discussed in curriculum documents such as the National Council of Teachers of Mathematics’ (2000) Standards. Instead, there seemed to be an assumption that teachers and their students were already aware of the criteria for judging mathematical writing. However, this is rarely the case. As one of Doerr and Chandler-Olcott’s (in press) teachers stated, “there was no discussion at all about writing, what makes it good, what makes it acceptable, and what makes it mathematically correct”.
It is not a simple process of identifying those features that make up a “good” piece as opposed to the features of a “bad” piece. Many factors influenced what was being written as well as whether the pieces of writing conveyed their intended meaning adequately or extremely well. It is also known that demographic characteristics such as gender and ethnicity may influence how students choose to express themselves mathematically (Meaney, 2005b, 2006a). For example, Meaney (2005b) found that senior high school students embedded their algebraic responses within a narrative depending upon whether they answered correctly, their gender and the decile level of the school they attended, as well as on the actual question asked. There is therefore a need to identify some of the general issues that would be addressed in a piece of writing before considering how adequately they were addressed.
After analysing the texts written by students aged between seven and 13, Wilkinson, Barnsley, Hanna, and Swan (1980) proposed a model for assessing students’ development in writing. It had four components that all contributed to the quality of a piece of writing. These were:
- Cognitive: the writer’s awareness of the world: one’s ability to describe, interpret, generalise, and speculate
- Affective: the writer’s awareness of emotions and feelings of self and other people, including the reader and one’s environment and awareness of reality
- Moral: the writer’s awareness of a value system, attitudes, and judgements
- Stylistic: the writer’s awareness of syntax (the way words are organised), verbal competence, text organisation, cohesion, awareness of reader, and appropriateness of text. (Winch, Johnston, March, Ljungdahl, & Holliday, 2004, pp. 182–183)
The model is interesting because it places value not just on the stylistic features but also on what is being written about, as well as the writer’s awareness of their own and others’ responses to what is going on. However, all of these features would not be relevant to considering what constituted a “good piece of mathematical writing”. This is because writing in mathematics occurs to meet specific needs. As Burton and Morgan (2000) stated, “[t]he language used in mathematical practices, both in and out of school, shapes the ways of being a mathematician and the conceptions of the nature of mathematical knowledge and learning that are possible within those practices” (p. 445).
The work Doerr and Chandler-Olcott (in press) did with middle school teachers of mathematics also encompassed considering what were the features of good mathematical writing. The features these teachers identified are given in Table 5.
Table 4 Teacher-generated description of good mathematical writing (from Doerr & Chandler-Olcott, in press)
Characteristics of good math writing
|
|
This list is quite explicit. However, it could well be that if the word “math” were replaced with another subject area such as social studies the list would not need to change in any particular way. There is little in this list that really seems to suggest that good mathematical writing has specific features connected to the writing being about mathematics.
Our teachers had also commented on students’ poor use of grammar when writing in mathematics. T5 had found it hard to let students write in his mathematics class because he was conscious of how much their reo Māori was influenced by English. He therefore felt that having them write might reinforce this inappropriate use of te reo Māori. T2 also described her students’ poor writing about probability:
It is something, the subject of probability, what they do is more or less explain what they saw from the data and what I had seen was the writing was erratic. They wanted to put every word they could think of on paper and who cares about grammar. (T2, Interview November 2007)
So the stylistic features that were identified in Table 5 were also issues for the teachers in our research. This is discussed in more detail in the next chapter.
What we did and what we found out
In the staff meeting in September 2007, the teachers discussed the question of what constituted good mathematical writing. Each teacher examined a group of students’ writing from their own class. They then shared their answers to the following questions:
- What is a good piece of writing?
- What is a poor piece of writing?
- What are the features that make it a good piece of writing?
- What strategies can be used to improve students’ writing?
T9 stated that he had difficulty determining a good piece. Sometimes the mathematics was better, sometimes the mathematical diagrams used for the explanation were better, sometimes the measurements were added (mm squared or not), and sometimes the written explanations were better although the maths was not as detailed as some of the others. In the samples he looked at, all of the students came up with the right answer. Four examples of this set are shown in Figure 25. The original activity had required the students to do the following:
- [Write] for someone who doesn’t know how to do it.
- Write why you should do it like that.
- At the end write anything else you know about Pythagoras.
Figure 24 Samples of T9’s class’s work on Pythagoras


T9 felt it was difficult deciding what was a quality piece of writing because there was a need to consider the student’s:
- written explanation
- diagrammatical representation
- mathematical accuracy using appropriate symbols and measurements.
Although this list is simpler than that provided by Doerr and Chandler-Olcott’s (in press) teachers, it is connected explicitly to the mathematical nature of the writing. It is possible to use these ideas to redesign the model of Wilkinson et al. (1980), so that it is more appropriate for mathematical writing. If this were done, then the components could be:
- mathematical: the writer’s awareness of the mathematical ideas and how they relate to what is being discussed
- integration of modes: the writer’s awareness of how to make use of a range of different modes to increase the clarity of the ideas they were presenting
- stylistic: the writer’s awareness of mathematical writing conventions in a similar way to the stylistic awareness described by Wilkinson et al. (1980).
Students who were good in one area of writing about mathematics were not necessarily good in another. To improve this group of students’ mathematical descriptions and explanations, then, all the different needs would have to be catered for. So some students would need support to ensure that they provided appropriate measurements and symbols. For others, it would be looking at the vocabulary and discussing more appropriate choices. For others, it would be discussing with them what had gone on in their head that had not been quite right. This is a mathematical issue that needed to be dealt with. So the features of a good piece of writing about Pythagoras’ theorem must have the mathematics correct, must use diagrams and text clearly and concisely and must be able to integrate these into a coherent whole.
Some of the teachers felt that sometimes there was a sense that a student knew more than they were able to put down on paper. However, if the students were to use mathematical concepts in the next stage of their learning their justifications of these concepts need to be clearer. One of the reasons for concentrating on writing is that it is easy to see when students are able to show their ideas clearly because it is permanent.
In the final interviews, the issue of a quality piece of writing and how to achieve it was raised. T8, who was in charge of the junior section of the school, felt that this question needed more discussion, especially in regard to how to improve all students’ writing in mathematics. She felt that on the whole the good things that happen in the writing lessons in the language classes were not necessarily being transferred over to the mathematics class. Teachers were too easily satisfied with what their students produced as mathematical writing. With the project continuing into 2008, she felt that this would be worth spending more time on.
Given that the discussion about what was a “good piece of mathematical writing” did not include assessing students’ awareness of their own or others’ cognitive, affective or moral understanding of the world as was included in the Wilkinson et al. (1980) model, then this may be an appropriate starting place for further considerations.
Conclusion
Whakamārama and parahau were seen by the teachers as being an important part of the writing that students should be doing in mathematics. They saw them as having benefits to the students in supporting them to reflect on what they were learning. They also benefited the teachers because these types of writing would help them to understand their students’ thinking. However, the samples we had of explanations and justifications that combined different mathematical modes would not necessarily be easy to teach. This is because the ways they arranged the different types of information were not linear. The easiest to follow were those that used lines or arrows to link the different components. The clarity in the writing was linked to the tenor of the context of situation. If the writing was produced for a wide audience, it was more likely to be clearer. The exception would be if the writer anticipated referring to their own writing at a later date. If the writer was writing for someone who was aware of the problem and already had insights into how the solution could be achieved, then there was often a lot of information left out.
Explanations were those that provided information about how the problem was linked to its solution. Justifications provided information about the reasons for why they used a particular solution strategy. Some justifications were very implicit and a reader had to have a considerable amount of detail filled in in order to understand why a particular solution was adopted.
The complexity of relating the purpose of the writing to the audience can be related to the teachers’ beliefs about what was a quality piece of writing. These teachers felt it was important for the students to be confident in all the mathematical writing modes. They also realised that difficulties with how students presented their ideas could be related to their lack of understanding of mathematical concepts rather than mathematical writing skills. However, ideas about what constitutes a “good piece of mathematical writing” need to be explored further.
Web editor’s note: This report was published in two PDF documents. The second part of the report (PDF format) is available here





