Using home languages as a resource to enhance statistical thinking in a multicultural classroom
Sashi Sharma, Phil Doyle, Daniel Kumar, and Louis Marcelo (2024)
Introduction
Aotearoa New Zealand is a super diverse nation in terms of the ethnicities of its people and languages spoken. With an increased rate of immigration (New Zealand Immigration, 2018) from various parts of the world, the presence of multiple languages in many domains of social life is a reality. Individuals may identify with several nationalities or racial groups and may speak combinations or mixtures of several languages (Dockrell et al., 2022; Education Review Office, 2018). Consequently, classrooms are now places where learners have different linguistic and cultural backgrounds, where they may speak one language at home and another at school, where teachers and students may not share a common language or cultural background, and where some or all of the students are learning the language of instruction as a second language (Barwell, 2020; European Commission, 2015; Spoonley & Bedford, 2012). This diversity can be challenging for both teachers and students and carries profound implications for mathematics and statistics educators.Language challenges and strategies
It is well known that the language of mathematics and statistics, which is the focus of this study, poses a challenge to English second language students (Hunter et al., 2018; Jhagroo, 2015; Latu, 2005; Lesser & Winsor, 2009; Morris, 2021; Trinick et al., 2016). Latu (2005) noted that word problems involving mathematical implication and logical structures such as conditionals and negation were a particular issue for Pasifika students. Latu also noted that English words are sometimes phonetically translated into Pasifika languages to express mathematical ideas when no suitable vocabulary is available in the home language. The same point was made by Morris (2021) in his study with Tongan students. Concepts such as “probability”, “randomness”, and comparative terms like “very likely”, “probable”, and “almost certain” have no equivalents in Tongan language. Recognising and appreciating the diverse language and cultural backgrounds of learners can promote the development of positive identities and, thus, can engage learners in their learning process (European Commission, 2015; Hunter et al., 2018; Jhagroo, 2015; Trinick et al., 2016). Research indicates that students who have a high level of proficiency in their first language and who develop a similar level of proficiency in the classroom language tend to outperform monolingual students in mathematics (Araujo et al., 2018; Cummins, 2017). In contrast, students who do not develop a sufficient level of proficiency in any language tend to underperform in mathematics (Dockrell et al., 2022; Mady & Garbati, 2014; Robertson & Graven, 2020). Additionally, mathematics education research has identified that a student’s first language(s) can serve as a resource for thinking and communication as students simultaneously learn and develop proficiency in the language of instruction and learn mathematics (Lesser et al., 2016; Trinick et al., 2016). Planas and Setati-Phakeng (2014) describe three perspectives that impact on the development of language policies and multilingual classroom practices: language-as-problem; language-as-right; and language-asresource. The language-as-problem perspective considers language as something that creates challenges that need to be resolved. In this view, teachers may view students’ limited English as a limitation to be overcome through a focus on intensive language teaching. Language-as-right emphasises the protection of minority language groups since everyone has the right to be educated in their home language. These authors further note that, while language-as-right supports the use the students’ home languages as the language of learning and instruction, this initiative is often paired with the stigma of the home language being a “non-English” language. Here, pedagogical strategies and policies based on language-as-problem and language-as-right can have unintended effects on different language groups of students by decreasing their access to classroom learning opportunities and interaction. By contrast, the language-as-resource perspective addresses both the stigma and the problem through actively encouraging the use of multiple languages during mathematics. New trends in multilingual education have provided opportunities to change traditional approaches to teaching and to explore the potential advantages of translanguaging (Cummins, 2017; Duarte, 2019). Translanguaging is a dynamic process whereby multilingual users mediate complex social and cognitive activities through strategic and flexible employment of the multiple communicative resources they possess (Canagarajah, 2018). These communicative resources include gestures, objects, everyday experiences, home language, video clips, and a mixing of languages and mathematical representations (Moschkovich, 2018; Tai, 2021). Other researchers, such as Farsani (2016) and García and Leiva (2014), have employed the term “translanguaging” to depict language fluidity and movements rather than linearity during teaching and learning. Both the classroom teacher and learners translanguage constantly to co-construct meanings, mediate understanding, and to increase participation in the classroom. In Aotearoa New Zealand, a common approach to addressing underachievement in mathematics of those students for whom English is a second or even third language is often to try to transition them to learning completely in English (Sharma, 2018). In this scenario, active use of other languages is seen as a hindrance rather than a help. In contrast, our study adopted a language-as-resource approach consistent with New Zealand understandings of culturally responsive pedagogy (Averill et al., 2009; Education Review Office, 2018; Hunter et al., 2018) and The New Zealand Curriculum (Ministry of Education, 2007, p. 9) principles of cultural diversity and inclusion.Probability as a context for study
Statistics and probability involve understanding numbers in context (Watson et al., 2018). The ideas within probability in particular can be challenging because of the way they are intertwined with everyday language and culture (Groth et al., 2016; Lesser & Winsor, 2009) and cultural values (Dinan Thompson et al., 2014; Farsani, 2022; Lesser et al., 2016) meaning teachers need to be sensitive to the implications of cultural differences, including those associated with religion (Morris, 2021; Sharma, 2014). For example, a number of students in Sharma’s (2014) study drew upon their religious beliefs in thinking about everyday probability in scenarios to do with childbirth and winning lottery numbers. Moreover, the concepts of probability do not develop incidentally or through maturation; rather, students need to be provided with planned probability learning experiences that include hands-on activities and simulations, not abstraction (Batanero et al., 2016; Groth et al., 2016). Games have always played an important role in learning mathematics as they encourage mathematical thinking (Brown & Bolstad, 2018; Dinan Thompson et al., 2014; Sullivan, 2020). Research has shown that game-based learning enriches the learning environment, improves the students’ performance, increases the students’ motivation, provides the opportunity to work with the group, and provides a fun learning environment (Chow et al., 2011; Koparan, 2019; Sullivan, 2020). Additionally, games help in creating opportunities for independent learning and overcome challenges for English language learners. Children who are reluctant to participate in other mathematical activities because of language barriers will often join in a game, and so gain access to mathematical learning as well as engage in structured social interactions (Chow et al., 2011; Sullivan, 2020). In the realm of probability, an intriguing recommendation for instruction is to use culturally diverse games to promote students’ understanding of probability (Dinan Thompson et al., 2014; McCoy et al., 2007; Naresh et al., 2014). Teachers are often recommended to develop contextual problems and other materials based on their understanding of what students would be familiar with (Barwell, 2020; Lesser & Winsor, 2009; Sharma, 2018), but teachers’ assumptions about familiar contexts may need to be revisited for culturally and linguistically diverse learners (Lesser & Winsor, 2009). Some students in Sharma’s (2018) study interpreted Kiwi birds as Kiwi people. Hunter’s (2016) work illustrates that a culturally responsive approach can help break down barriers that inhibit many Pasifika students’ engagement and achievement in mathematics. In our collaborative study, games were used to explore the basic probability knowledge of Year 9 students and to enable discussions around mathematical ideas in a culturally responsive environment.Research design
Design-based research theory (Cobb & McClain, 2004) was used to conceptualise our collaborative study. Design research is a cyclic process with action and critical reflection taking place in turn (Cobb & McClain, 2004; Nilsson, 2013). There are benefits for both teachers and researchers when undertaking a design research partnership: the research plan can be flexible and adaptable to unforeseen effects or constraints (Nilsson, 2013). Further, all participants are equal partners in the research process with no hierarchy existing between researchers and practitioners (Shaughnessy, 2014). The approach fosters theory and practice development. The following research questions guided our study:- How do multilingual Year 9 students negotiate communication in small-group and whole-class settings when working on probability tasks?
- How might teachers draw on home languages, contexts, and cultural experiences to enhance the probability understanding of multilingual students?
Research phases
To answer the research questions, the two cycles of the three design research phases were worked through: a preparation and design phase; a teaching phase; and a retrospective analysis phase.Phase 1: Preparation and design for the teaching phase (Term 2, 2020)
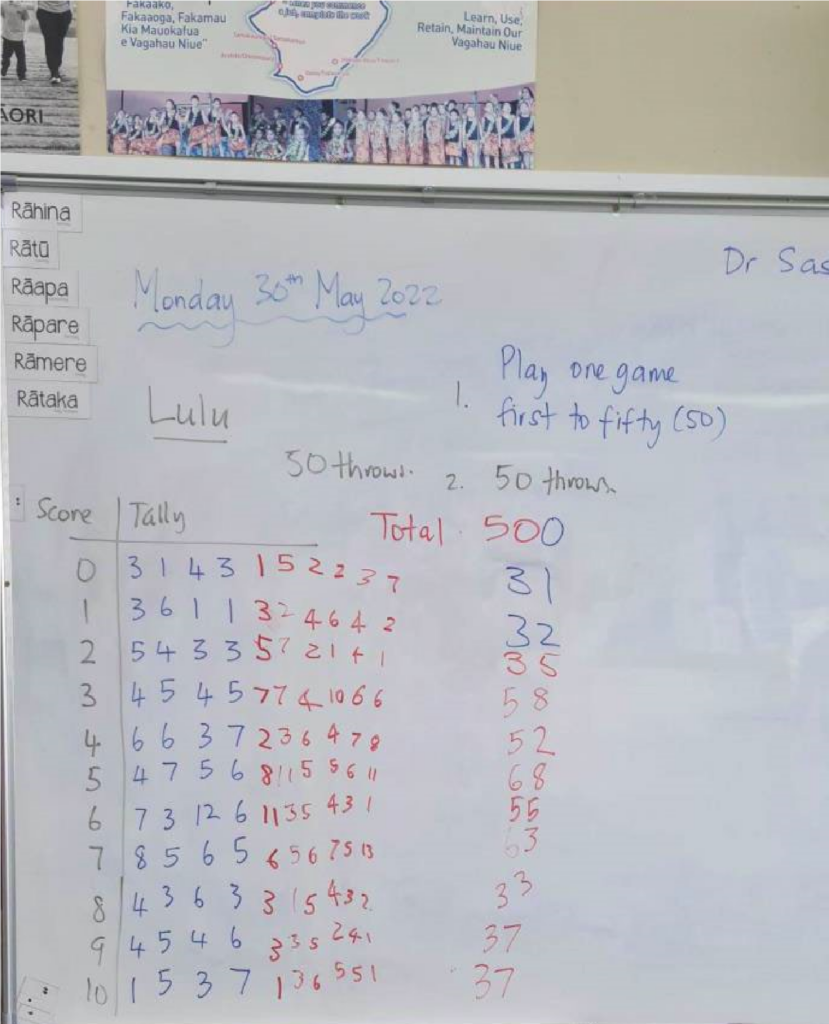
The preparation phase began with a discussion between the teachers and the researcher about research findings on language challenges, translanguaging, and language-as-resource pedagogical strategies for English second language learners. The research team also hypothesised how dialogue and statistical activity might unfold as a result of a planned probability lesson sequence. This process helped develop a deeper shared understanding of the challenges teachers might face and the opportunities they could create, as well as potential strategies that teachers could use to reduce obstacles for student learning. During phase one of the research project, we played and discussed three games: Ashbii (McCoy et al., 2007); Rock-Paper-Scissors (Koparan, 2019); and Lulu (Naresh et al., 2014). The teachers selected Ashbii and Lulu games because these related to students’ cultural experiences that are difficult to integrate in a/their mathematics class. The games provided opportunities for students to attend to meanings of probability concepts rather than practise rote formulas in textbook exercises.Phase 2: Teaching experiments (Term 2, 2021; Term 2, 2022)
The teaching took place as part of regular classroom statistics lessons in two largely Pasifika student dominated Year 9 classes (each comprising about 25 students). Students carried out an exploration and analysis of the Lulu and Ashvii games over three lessons. Students collected experimental data, organised it into tables and graphs, and compared it with theoretical probabilities derived from generating the sample space for the Lulu game. As an initial approach, students with the same first language were grouped together to work on tasks; this approach is consistent with Planas and Setati-Phakeng (2014), who found that grouping students according to their dominant language encouraged the use of their first language. The teachers intentionally encouraged students to use multiple languages (home language, everyday language), diagrams, and representations to explain their thinking. A research assistant who spoke two or more languages was present during the teaching sessions. This assistant helped the teachers by, for example, providing real-time translations, encouraging home language use in group discussions, taking field notes, and audio recording the class sessions. Students were used to having other adults in the classroom, so their presence did not have any negative impacts on the class. The teaching experiments were delayed on several occasions due to the Auckland lockdowns for COVID, and other issues that impacted on the school and teachers.Phase 3: Retrospective analysis (Term 3, 2021; Term 2, 2022)
The three teachers and the researcher performed a retrospective analysis together after each lesson to reflect on and refine the lesson plans while the teaching experiment was in progress. The updated lesson plans were used for teaching future lessons. In addition, the team analysed the whole lesson sequence on completion of the teaching experiment. Teachers were given the opportunity to reflect on the implementation process and identify what they would do to enhance student learning and interest differently.Data collection approaches
During the teaching experiment, audio recordings of student group discussions were made. Each teacherresearcher also kept field notes of specific events that took place during the teaching for data collection period. Field notes helped teachers identify and keep track of which strategies seemed to work well for students and which ones were less successful. For example, Teacher A reported that movement between modes (verbal and non-verbal) provided students with rich opportunities for active participation rather than simply writing definitions in their notebooks. During the retrospective analysis phase, the teachers reflected on the implementation process. Data also came from audio recordings of planning meetings, whole-class student group discussions, student interviews, and teacher notes.| Research question | Data sources | Analysis approach |
|---|---|---|
| Negotiating communication in small-group/wholeclass settings | Audio recordings of teaching and learning activities Field notes of classroom events Video-stimulated recall interviews with students Student journal entries Student work samples | Thematic analysis Verbal and non-verbal communication and meaning-making processes Team retrospective analysis |
| Language, contexts, cultural resources, and language-based strategies | Field notes of significant group and whole-class events Video-stimulated recall interviews with students Audio-taped teacher planning/analysis meetings Student work samples Student journal entries | Strategies for enhancing student probability learning Retrospective analysis |
Data analysis
Discussions with students about key events from their group discussions were transcribed. The transcripts were subjected to thematic analysis and coding (Braun & Clarke, 2022) to identify emergent thematic patterns of relevance to the research questions, such as the nature and frequency of translanguaging communication practices from students’ home language to everyday English, and to the language of probability. In the context of probability learning, translanguaging was taken to include the use of different modes (reading, writing, and speaking) as well as diagrams, tables, graphs, and gestures. This process involved each member of the research team independently reading and re-reading the transcripts and noting down initial themes or points and associated examples of these in practice (Sharma et al., 2011), before coming together as a team to discuss and agree on the themes for the research question/s. The next step involved gathering all data relevant to the agreed themes. Over the two teaching experiments and cycles of design research, ongoing analysis helped refine the specifics of each theme to tell a comprehensive, overall story. Conjectures generated in one lesson/classroom were tested against data collected from other lessons and classrooms. Through this process, we distilled the characteristics of effective teaching activities and data collection in multilingual classrooms and finalised the teaching sequence.Ethical considerations
Ethical approval for the research was gained from the University of Waikato’s Division of Education Research Ethics Committee. Participation in the study was voluntary for teachers, students, and parents/whānau. The ethics application was developed in consultation with the teachers. We followed all ethical protocols including informed consent, the right of withdrawal, the right to confidentiality, and the preservation of anonymity through the use of pseudonyms in referring to the individuals within the school. We expanded our group to include a member of faculty who had completed their Grad. Dip TESSOL and who has an interest in supporting students using their home languages. This teacher provided translation support if the need arose.Key findings
Using a language-as-resource perspective in the mathematics classroom and supporting English second language students in developing language proficiency in the main language of learning and teaching is complex. However, each of the researched findings below would, we argue, contribute to making mathematics teaching and learning more inclusive.Using cultural games
Games have always played an important role in learning mathematics in the classroom (Dinan Thompson et al., 2014; Koparan, 2019; McCoy et al., 2007). Cultural games, as a subset, are those games that are specific to a culture and use knowledge of a particular group of people. In our study, we used the Lulu game, which originated in Hawaii (Naresh et al., 2014) but adapted it to the local context, with students who were not Hawaiian or speaking that language We chose this game from a selection that we played together because we thought students would be familiar with it and/or could easily learn it. Another reason was that e- lulu means “to shake” in Samoan. The game uses four two-sided dice as shown in Figure 1. We used glass stones for dice. The stones were unmarked on one side and marked with one, two, three, or four on the other side. FIGURE 1 Two-sided dice for the Lulu game
There are two versions of the game. We used the basic version of the game due to time constraints and difficulty level. The challenge version could be explored by Year 10 or Year 11 students. The game is played in pairs or groups of four. Each player throws all four stones at random and counts the dots they can see. The first player closest to 50 points in the game wins. FIGURE 2 Instructions and focus questions on slide
The glass stones are thrown at random on the table, and the throws are named as follows:
|
It helps people learn the basics of probability and it is also fun at the same time.
I like the games because it helped towards my probability learning in a fun way.
It was a creative way of learning about probability. Different ways of showing sample space and calculating probabilities.
Students who were reluctant to participate in other mathematical activities because of language barriers often joined in the game. The teachers had supported students to use their home languages by using homogeneous grouping and the game manipulatives/resources provided further support for communicating their thinking. The small-group setting meant that students shared and developed mathematical ideas as part of engaging in structured supportive social interactions. These findings resonate with those of Chow et al. (2011) and Dinan Thompson et al. (2014) who also found games provided learning environments that were educational and fun. Pre- and post-assessments, designed by the teachers and out of 10 marks, were conducted to evaluate student understanding of probability. These tests were designed by the teachers and both were out of 10 marks. In both cases, the middle 50% scored between three and six out of 10. In the posttest, 50% of students scored five and above while in the pre-test it was four and above. Teachers noticed that the interest of some students waned when they were asked to stop playing the game and start thinking about the outcomes and results of the game. Teachers sustained students’ interest by maintaining links between the game (experimental probability) and the thinking (theoretical probability). This was done through careful questioning, class discussion, and student reflection on the game, the theory behind it, and strategies students could employ to improve their chances of winning the game. For example, a player whose score was 47 might decide to stop since the chances of obtaining a score greater than a three was much higher than that of three or less. Students could use their probability thinking to choose to take risks or play it safe to accumulate as many points as possible.Language considerations
The teachers used a range of language approaches to address the linguistic challenges that arose in our study. These included: students using their home language; attending to the lexical ambiguity of probability terms; and the use of non-linguistic cues.Students using their home language
Teachers supported their students to use their home languages, and (or alongside?) everyday English and mathematical/statistical English to discuss and develop their understanding about statistics/probability ideas. The quotes below reflect why the students thought using their home language was valuable:We respect and understand each other’s language and culture. I know the language and background of my colleagues, which makes me connect with them.
We can understand our home language … cultural background. It is good for future generation otherwise we will forget about our culture.
The quote below illustrates that not all the students wanted to use their home language; some were more focused on doing well in class assessments that were in English: I don’t want to use my home language in [the] mathematics class. Try to use English so I can do well in the test.Teacher support for home language
While research shows that many teachers believe using home languages is detrimental to learning (Edwards, 2012; Mady & Garbati, 2014; Planas & Setati-Phakeng, 2014), this was not the case for the study teachers who could see the educational value of learners being able to use their home language(s). They identified that students’ first language(s) can serve as a resource for thinking and communication. Hence, they viewed home language use as pedagogically beneficial. This view is reflected in the following quote which also explains that teachers themselves sometimes code-switched:It is a waste of time asking students not to use their home language. They use their home language all the time. Even teachers sometimes code switch to explain a concept or to get student attention.
However, teachers’ use and perceptions of the value of a particular language in different settings varied. Teachers deployed English in the whole discussions because not all students shared the same home language and English was familiar to all students. The following quote indicates that students recognised the different teacher expectations for language use in group and whole-class settings. That is, they recognised that their teachers supported translanguaging:Sometimes we use Samoan in groups. When I present to the whole class, I am required to use English. (Student comment)
These findings concur with those of Planas and Setati-Phakeng (2014) who reported that students used their home language in small-group settings but not in whole-class discussions. It is noteworthy that, over time, the teachers began to use more Pacific words. The use of “talanoa” is an example of this (Vaioleti, 2013).Attending to the lexical ambiguity of probability terms
Another finding relates to lexical ambiguity of many probability terms. Students were often confused when they were introduced to a word from their everyday register that had a different or more technical meaning in the academic probability register:Some words are pretty hard … another meaning … like words in everyday English … some words we have never heard confusing for us. (Student comment)
Specific examples included “random” and “in the long run”. Informally, random is defined as being strange, unusual, or unexpected (Cambridge University Press, n.d.) whereas in statistics classrooms, randomness relates to predictability of outcomes. It is understandable, then, that some students might have perceived the random process of throwing four glass stones and getting a total from the throws (in the context of Lulu game) as something not normal as reflected in the response below:I am not sure … it can mean something that does not always happen.
When asked to explain the phrase “in the long run” in the context of co-ordinating experimental results and theoretical probabilities, responses were:The longest run or fastest to flip the dice.
Actually, you don’t know, it could be 50–50 chance.
Both the above responses are inappropriate in the Lulu game context. One teacher addressed student confusion using a Lulu applet whereas another explicitly referred to long run as “long term” to avoid confusion around the phrase. These findings about the challenges of lexical ambiguity parallel those of Kaplan et al. (2009) and Lesser et al. (2016). This said, the teachers discussed that some ambiguity can be a resource for discussion between teachers and students. Movement between registers is a necessity for students, and teachers can use ambiguous terms as a focus for discussion and guidance in this process (Barwell, 2020). One teacher explained the value in this approach was that it could lead to greater awareness of language among students and the development of thinking key competency (Ministry of Education, 2007) which is often not explicit in mathematics teaching and learning. Overall, teachers concluded it is important to emphasise that some terms have multiple meanings depending on if they are used in the everyday register or a statistical register.The use of non-linguistic cues
Providing non-linguistic cues such as visual diagrams, demonstrations, physical items, and gestures can make more complex language accessible for learners as these are less language-dependent modes. Farsani (2016) suggests that having multiple entry points and scaffolds is helpful in a direct way for communication and in an indirect way in creating a low-anxiety environment. Teachers were aware of this and deliberately used a range of non-linguistic cues in conjunction with verbal communication. For example, Teacher A drew diagrams and wrote questions, instructions, and explanations on the whiteboard. He checked before proceeding that the students could read and understand what was written on the board before he started talking. The following table was posted on the whiteboard by Teacher A to explain the scoring rules for the Lulu game.| Sides facing up | Points |
|---|---|
| Hu-li la-lo—all stones are face-down | 0 |
| Hu-ka-hi hu-i i-lu-na—one stone is face-up | 1–4 |
| E-lu-a hu-li i-lu-na—two stones are face-up | 3–7 |
| E-ko-lu hu-li i-lu-na—three stones are face-up | 6–9 |
| E-ha hu-li i-lu-na—all four stones are face-up | 10 |
| 4-3-2-1; 4-3-2-0; 4-3-0-1; 4-3-0-0; 4-0-2-1; 4-0-2-0; 4-0-0-1; 4-000; 0-3-2-1; 0-3-2-0; 0-3-0-1; 0-3-00; 002-1; 0-02-0; 0-0-0-1; 0-0-0-0. |

FIGURE 5 Work sample of one student showing possible outcomes using a table
| Possible outcomes for a turn | Score |
|---|---|
| 1, 2, 4 | 7 |
| 1, 3, 4 | 8 |
| 1, 2, 3 | 6 |
| 1, 2, 3, 4 | 10 |
| 2, 3, 4 | 9 |
| 2, 3 | 5 |
| 2, 4 | 6 |
| 1 | 1 |
| 1, 3 | 4 |
| 1, 4 | 5 |
| 2 | 2 |
| 3, 4 | 7 |
| 3 | 3 |
| 1, 2 | 3 |
| 4 | 4 |
Teacher practices
In addition to the points raised above, teachers used a range of strategies to facilitate student statistics learning and language development. Themes that arose from our analysis were: teacher modelling; reading and writing in support of deeper learning; support for collaborative learning; using real-life contexts; and building positive relationships.Teacher modelling
The teachers initially engaged the students by presenting the game scenario. They asked their students to read through the Lulu game description and make sure they understood what was required. Two teachers then played a round of the game. They read the outcome using Hawaiian text; for example, they said E-ha hu-li i-lu-na when all sides of the glass stones were up to show language as resource perspective. The teachers played the game five times and recorded the results in a frequency table as shown below in Table 3. Teacher C was declared the winner with a total of 21 points.| Round 1 | Round 2 | Round 3 | Round 4 | Round 5 | |
|---|---|---|---|---|---|
| Teacher A | 0 | 3 | 2 | 10 | 1 |
| Teacher C | 6 | 2 | 0 | 4 | 9 |
Reading and writing in support of deeper understanding
Supporting English second language students in reading and writing is vital in multilingual settings (Jones & Seilhamer, 2019). All teachers mentioned students’ difficulties with reading, speaking, and writing in English in Phase 1 of the research project. They considered this affected students’ ability to engage in class work and formal assessments because students could not explain or justify their thinking when answering test questions. The teachers used deliberate strategies to teach vocabulary in varied and supportive ways. For example, they helped their students to attend to the probability vocabulary in relation to the Lulu game: experiment (playing the game of Lulu); trial (one toss of the stones); outcome (the way the stones landed); experimental data (scores of individual players); and experimental probability (probability of the collected data). Teachers used student feedback to write definitions of trial, frequency table, and tally chart on the whiteboard as follows:| Frequency table: a table that uses numbers to show how many items are in several categories or how often several things occur (for example, the number of students with black, brown, red, and blonde hair). Tally chart: a method of recording frequency of data using stroke marks (for example, ////). Trial: one instance of carrying out an experiment (for example, flipping a coin 10 times). |
The teachers also provided writing frames and cloze activities to help students analyse data and draw conclusions. For example, the following writing frame was provided for writing conclusions:
If we played the game 200 times, we would expect approximately …….… sevens in 200 tosses. The law of large states for a sufficiently large number of trials, the ………. will more closely reflect the …….…
The use of writing on the board to aid the language learning and comprehension of the students concurs with earlier work by Sharma et al. (2011) in a different context and that of Jaafar (2016) in letter writing activities when learning calculus. Jaafar (2016) claimed that writing activities not only help students cement mathematical knowledge, deepen understanding, and develop appreciation for the rigour and concision of mathematical language, but also enable them to develop learning habits essential to their success in any field. Sharma et al. (2011) found that writing words/vocabulary on the board reinforced learning for Pasifika students.Support for collaborative learning
All three teachers used collaborative learning strategies when implementing the probability sequence of three lessons. As noted earlier, the students worked in homogeneous language groups to discuss the ideas and questions they had relating to lesson activities. This allowed the students to ask questions and get feedback in a safe learning environment as pointed out by the following student:Using home language was very helpful, especially for someone like me who kind of struggles in maths. I mean interpreting the questions. Other boys talk me through the instructions … use simple language so I understand more.
The above quote indicates that students found working in their home language helpful. The next student quote indicates that relationships with peers played an important role during group work:We feel confident discussing ideas with other boys if we know them and relate well with each other. However, it is not easy to work in groups if we do not know each other well.
The following student quote indicates that the student felt comfortable asking questions in a class if they had a good relationship with their teacher and peers:I feel confident about asking question in class if I know my teacher well and have good relationships with other boys.
However, some students were not always eager to share their ideas in front of the whole class. To help address this, we asked students to share their thinking with a peer before asking them to share ideas with the whole class. Brown et al. (2009) and Goldenberg (2008) found that when English second language learners work alongside a partner they can benefit from opportunities for interaction and support that enhance their learning.Using real-life contexts
Hipkins et al. (2022) explain that appropriate contexts help students enrich their worldview and make sense of lessons. When students explore statistics through a meaningful context, they are able to derive meaning of abstract concepts, such as variation, and to see that statistics is an integral part of their lives (Lesser & Winsor, 2009; Watson et al., 2018). As mentioned earlier, the teachers in this study were aware of making connections to the experiences and cultures of their Pasifika students as reflected in the following quotations:Using games made more sense to students. They were more engaged and motivated in the lesson. Students can get disengaged when they do not see relevance. (Teacher C)
Another teacher commented on the importance of asking students to bring games that they play at home:Next year probably I will ask the boys to share games that they play at home. This will also help build school and home partnerships which is one of our goals. (Teacher B)
The findings parallel those of other statistics educators. According to Lesser and Winsor (2009), the most important clue to deduce the meaning of a word or sentence is generally its context, and when students find context meaningful, it increases their motivation to learn and communicate. Goldenberg (2008) claimed that statistics is a more natural vehicle for context-embedded instruction than mathematics, hence contextembedded instruction can have benefits for teaching English language learners statistics.Building positive relationships
In the Pacific culture, the nature of the relationship between the teacher and student plays a pivotal role in knowledge creation (McDonald & Lipine; 2011; Reynolds, 2022). This relationship is underpinned by reciprocity, mutual trust, and commitments from both the teacher and student. The teachers in our collaborative study were aware of building positive relationships with students as reflected below:I don’t speak Samoan well. The little bit of Samoan I do speak I have picked up from the boys and other teachers. I could ask the students to teach me, and then let them make fun of me when I mispronounce terms but it does have advantage, it helps build positive relationships. (Teacher B)
Although I teach students not to get off topic during group work, at times the boys tend to get a little more curious about tangential topics and start telling personal stories. Sometimes I allow it as it helps build sort of relationship, you get to know the students’ interest. (Teacher C)
Teacher B’s reflection reminds us of the reciprocity principle (Saunders et al., 2018). Teachers can learn from students. In fact, he uses his own weaknesses in Samoan as an opportunity to empower students by honouring their home language and ultimately fostering positive relationships. Teacher C sometimes listened to personal stories because stories helped the teacher connect to what students already know, their interests and their curiosities could form the basis of future learning. Similar points were made by McDonald and Lipine (2011) and Reynolds (2022). McDonald and Lipine studied Samoan high school students from six schools and found that a positive teacher–student relationship was one of the important factors in the engagement in learning and academic success of Samoan students. Reynolds signalled that having positive relationships with Pacific students helps teachers create a safe space for students to engage in learning.Implications
Language diversity of students in schools is expanding worldwide and educators need to improve how they teach these learners. The following implications arise from this study.Implications for teachers
Games not only provide opportunities for students to learn probability concepts, but they can also sustain student interest and motivation. Games can provide an interesting context for discussing probability concepts, but their use requires teacher guidance for students to think deeply about the notions of sample space, representations for sample spaces, and experimental and theoretical probability. Games can help teachers highlight and value student culture in context in a mathematics classroom. The Lulu game is an example of a cultural game that can provide rich possibilities for engagement and learning. Findings suggest that teachers should take particular care with the way probability concepts are worded, including “random” and “in the long run”. These and phrases such as “at least” are likely to prove difficult, and particularly for English language learners. Teachers could use bilingual resources as suggested by Lesser and Winsor (2009) to clarify language and reveal misconceptions rooted in language. Gestures and language modes can complement each other and be used together as resources for mediating and scaffolding teaching and learning. Teachers could usefully think of them as a single system that is larger than either of them when considered separately. Given this, it is also important that language policies in Aotearoa New Zealand acknowledge the mixing of gestures, oral and written language modes, and assist teachers to constructively make strategic use of these in the mathematics classroom, particularly in the context of a multicultural and multilingual environment. We believe that our illustration of the language-as-resource orientation in action will benefit teachers who wish to create mathematics learning opportunities where students can use the language they know best in the development and communication of their mathematical thinking. The teaching sequence developed within the study provides an empirically grounded example that teachers could adapt to their local circumstances. Our findings on language-based strategies also have the potential for use in other school subjects such as science and in other multicultural contexts.Implications for teacher education
Although Aotearoa New Zealand is multilingual, many teachers are monolingual and/or do not have experience in or strategies for working with children whose home language is not English. As language is the main medium through which teaching and learning takes place, mathematics teachers need access to professional development opportunities (at pre- and in-service levels) that clarify how academic language works in the mathematics classroom. Initial Teacher Education providers will be interested in this research. Understanding the challenges teachers face in the classroom when teaching statistics to learners with a range of home languages and language proficiencies will assist teacher education institutions to better equip teachers for a multicultural classroom.Implications for research
The teachers in the study used a variety of linguistic strategies that qualify as translanguaging (Duarte, 2019). These strategies included using visuals, objects, gestures, and movement between languages. Teachers used these strategies to help students to make sense of the content and to elicit students’ thinking but not necessarily to support students’ first language. More evidence on the benefits of translanguaging in statistics education needs to be gathered, ideally in linguistically diverse mathematics classrooms. Furthermore, research on translanguaging as a tool for assessing students’ mathematical knowledge is necessary to clarify its benefits when used in formative and summative assessments. Future research could explore the use of terms such as “in the long run” that are likely to prove difficult to students, and particularly English language learners, and the use of bilingual resources to increase the participation of English language learners and assess their understanding of alternative phrases to inform teaching for all learners.Summary/conclusion
Collaborative research philosophies and methodologies can be integrated in classroom-based research. Exploring and reflecting on a lesson sequence using a game context helped us develop both content and professional knowledge. Given breadth of dissemination, we consider that students and teachers have benefited from the study through the conscious effort we have made to share findings in a manner accessible to teachers. We need to generate new ideas for more collaboration and research between practitioners and researchers so we can improve outcomes for all our students. Culture and language play a vital role in what we perceive as good or bad, it influences how we dress and what we eat. Even our basic expression of emotion is culturally dependent. However, when it comes to statistics, only a few studies have explored how cultural differences influence answers to everyday life problems or interpretation of findings. Teachers, curriculum developers, and researchers need to continue to work together to find ways to help all learners develop statistical thinking within the milieu of culture, language, teaching strategies, learning resources, and curriculum demands that characterise many mathematics classrooms.Information on research team members
To understand a multilingual education context, the research team included teachers and a researcher with diverse cultural backgrounds and professional experience of secondary classroom teaching across a range of linguistic and cultural contexts. Sashi Sharma is an associate professor in mathematics education at the University of Waikato. Her research is located at the intersection of mathematics and statistics with a particular focus on linguistic and cultural issues. Contact: sashi.sharma@waikato.ac.nz Phil Doyle is a deputy principal at De La Salle College. He was involved in a 2009–11 TLRI with Sashi. He contributed to the design of the project and provided ongoing support for the teachers in the project. Daniel Kumar is the school’s deputy HOD mathematics. Daniel participated as a classroom teacher. He contributed ideas and an important perspective to the project and actively shared successes with colleagues. Louis Marcelo is a mathematics teacher at the college. He co-planned and trialled the project teaching sequences in his classroom and participated in data analysis and dissemination.References
Araujo, Z., Roberts, S. A., Willey, C., & Zahner, W. (2018). English learners in K–12 mathematics education: A review of the literature. Review of Educational Research, 88(6), 879–919. https://doi.org/10.3102/0034654318798093
Arzarello, F., Paola, D., Robutti, O., & Sabena, C. (2009). Gestures as semiotic resources in the mathematics classroom. Educational Studies in Mathematics, 70(2), 97–109.
Averill, R., Anderson, D., Easton, H., Te Maro, P., Smith, D., & Hynds, A. (2009). Culturally responsive teaching of mathematics: Three models from linked studies. Journal for Research in Mathematics Education, 40(2), 157–186.
Barwell, R. (2020). Learning mathematics in a second language: Language positive and language neutral classrooms. Journal for Research in Mathematics Education, 51(2), 150–178. https://doi.org/10.5951/jresematheduc-2020-0018
Batanero, C., Chernoff, E., Engel, J., Lee, H., & Sánchez, E. (2016). Research on teaching and learning probability. Springer. https:// doi.org/10.1007/978-3-319-31625-3
Braun, V., & Clarke, V. (2022). Thematic analysis: A practical guide. SAGE Publications.
Brown, C. L., Cady, J. A., & Taylor, P. M. (2009). Problem solving and the English language learner. Mathematics Teaching in the Middle School, 14(9), 532–539. https://doi.org/10.5951/MTMS.14.9.0532
Brown, H., & Bolstad, R. (2018). Games: The social tools handed down by our tūpuna. Set: Research Information for Teachers, (3), 86–88. https://doi.org/10.18296/set.0125
Cambridge University Press. (n.d.). In Cambridge Dictionary. Random. https://dictionary.cambridge.org/dictionary/english/random
Canagarajah, S. (2018). Translingual practice as spatial repertoires: Expanding the paradigm beyond structuralist orientations. Applied Linguistics, 39(1), 31–54.
Chow, A. F., Woodford, K. C., & Maes, J. (2011). Deal or no deal: Using games to improve student learning, retention and decisionmaking. International Journal of Mathematical Education in Science and Technology, 42(2), 259–264. https://doi.org/10.1080/0020 739X.2010.519796
Cobb, P., & McClain, K. (2004). Principles of instructional design for supporting the development of students’ statistical reasoning. In D. Ben-Zvi & J. B. Garfield (Eds.), The challenge of developing statistical literacy, reasoning, and thinking (pp. 375–395). Kluwer Academic Publishers.
Cummins, J. (2017). Translanguaging in bilingual education. In O. Garcia, A. M. Y. Lin, & S. May (Eds.), Bilingual and multilingual education (3rd ed., pp. 117–130). Springer. https://doi.org/10.1007/978-3-319-02258-1_9
Dinan Thompson, M., Meldrum, K., & Sellwood, J. (2014). “… it is not just a game”: Connecting with culture through traditional indigenous games. American Journal of Educational Research, 2(11), 1015–1022.
Dockrell, J. E., Papadopoulos, T. C., Mifsud, C. L., Bourke, L., Vilageliu, O., Bešić, E., Seifert, S., Gasteiger-Klicpera, B., Ralli, A.,
Dimakos, I., Karpava, S., Martins, M., Sousa, O., Castro, S., Søndergaard Knudsen, H. B., Donau, P., Haznedar, B., Mikulajová, M., & Gerdzhikova, N. (2022). Teaching and learning in a multilingual Europe: Findings from a cross-European study. European Journal of Psychology of Education, (37), 293–320. https://doi.org/10.1007/s10212-020-00523-z
Duarte, J. (2019). Translanguaging in mainstream education: A sociocultural approach. International Journal of Bilingual Education and Bilingualism, 22(2), 150–164. https://doi.org/10.1080/13670050.2016.1231774
Education Review Office. (2018). Responding to language diversity in Auckland. https://ero.govt.nz/our-research/responding-tolanguage-diversity-in-auckland
Edwards, S. (2012). Knowing the learner: What do secondary mainstream teachers know about their English language learners, and why does it matter? New Zealand Journal of Teachers’ Work, 9(2), 107–118.
European Commission. (2015). Language teaching and learning in multilingual classrooms. Publications Office of the European Union. https://data.europa.eu/doi/10.2766/766802
Farsani, D. (2016). Complementary functions of learning mathematics in complementary schools. In A. Halai & P. Clarkson (Eds.), Teaching and learning mathematics in multilingual classrooms (pp. 227–247). Brill Sense Publishers.
Farsani, D. (2022). The name game: The role of cultural affordances in learning probability. For the Learning of Mathematics, 42(2), 17–18.
García, O., & Leiva, C. (2014). Theorizing and enacting translanguaging for social justice. In A. Blackledge & A. Creese (Eds.), Heteroglossia as practice and pedagogy (pp.199–216). Springer. https://doi.org/10.1007/978-94-007-7856-6_11
Goldenberg, C. (2008). Teaching English language learners: What the research does—and does not—say. American Educator, 33(2), 8–19.
Groth, R. E., Butler, J., & Nelson, D. (2016). Overcoming challenges in learning probability vocabulary. Teaching Statistics, 38(3), 102–107. https://doi.org/10.1111/test.12109
Hipkins, R., Tolbert, S., Cowie, B., & Waiti, P. (2022). Enduring competencies for designing science learning pathways. New Zealand Council for Educational Research. https://doi.org/10.18296/rep.0025
Hunter, R. (2016). ‘Bobbie maths’ raising Pasifika achievement Pacific. Policy Brief 1. Pacific Research and Policy Centre, Massey University. https://www.massey.ac.nz/documents/821/Policy-1-Bobbie-Maths.pdf
Hunter, R., Hunter, J., Anthony, G., & McChesney, K. (2018). Developing mathematical inquiry communities: Enacting culturally responsive, culturally sustaining, ambitious mathematics teaching. Set: Research Information for Teachers, (2), 25–32. https://doi. org/10.18296/set.0106
Jaafar, R. (2016). Writing-to-learn activities to provoke deeper learning in calculus. PRIMUS, 26(1), 67–82. https://doi.org/10.1080/10 511970.2015.1053642
Jhagroo, J. R. (2015). I know how to add them, I didn’t know I had to add them. Australian Journal of Teacher Education, 40(11). https://doi.org/10.14221/ajte.2015v40n11.6
Jones, S. A., & Seilhamer, M. F. (2019). Teaching the language of mathematics at three levels of an English-medium primary school. Oxford Review of Education, 45(5), 639–656. https://doi.org/10.1080/03054985.2019.1591944
Kaplan, J. J., Fisher, D., & Rogness, N. (2009). Lexical ambiguity in statistics: What do students know about the words: Association, average, confidence, random and spread? Journal of Statistics Education, 17(3). https://doi.org/10.1080/10691898.2009.11889535 Koparan, T. (2019). Teaching game and simulation based probability. International Journal of Assessment Tools in Education, 6(2), 235–258. https://doi.org/10.21449/ijate.566563
Krause, M., & Farsani, D. (2021). More than words: An integrated framework for exploring gestures’ role in bilinguals’ use of two languages for making mathematical meaning. Canadian Journal of Science, Mathematics and Technology Education, 22, 773–795. https://doi.org/10.1007/s42330-022-00253-y
Latu, V. F. (2005). Language factors that affect mathematics teaching and learning of Pasifika students. In P. Clarkson, A. Downtown, D. Gronn, M. Horne, & G. A. McDonough (Eds.), Building connections: Theory, research and practice (Vol 2, pp. 483– 490). Mathematics Education Research Group of Australasia (MERGA).
Lee, J., Lee, Y., & Amaro-Jimenez, C. (2011). Teaching English language learners (ELLs) mathematics in early childhood, Childhood Education, 87(4), 253–260. https://doi.org/10.1080/00094056.2011.10523187
Lesser, L. M., Wagler, A. E., & Salazar, B. (2016). Flipping between languages? An exploratory analysis of the usage by Spanishspeaking English language learner tertiary students of a bilingual probability applet. Statistics Education Research Journal, 15(2), 145–168. https://doi.org/10.52041/serj.v15i2.245
Lesser, L. M., & Winsor, M. (2009). English language learners in introductory statistics: Lessons learned from an exploratory case study of two pre-service teachers. Statistics Education Research Journal, 8(2), 5–32. https://doi.org/10.52041/serj.v8i2.393
Mady, C., & Garbati, J. (2014). Calling upon other language skills to enhance second language learning: Talking taboo about first languages in a second language classroom. Research Monogram, 51, 1–4.
McCoy, L. P., Buckner, S., & Munley, J. (2007). Probability games from diverse cultures. Mathematics Teaching in the Middle School, 12(7), 394–402. https://doi.org/10.5951/MTMS.12.7.0394
McDonald, L., & Lipine, T. (2011). Pasifika education policy, research and voices: Students on the road to tertiary success. New Zealand Annual Review of Education, 21(2011–2012), 143–164. https://doi.org/10.26686/nzaroe.v21i0.4047 Ministry of Education. (2007). The New Zealand curriculum. Learning Media.
Ministry of Education. (2024). Ministry funding deciles. https://parents.education.govt.nz/secondary-school/secondary-schoolingin-nz/deciles/
Morris, N. (2021). Learning probability in the Kingdom of Tonga: The influence of language and culture. Educational Studies in Mathematics,107(1), 111–134. https://doi.org/10.1007/s10649-020-10022-z
Moschkovich, J. (2018). Talking to learn mathematics with understanding: Supporting academic literacy in mathematics for English learners. In A. Bailey, C. Maher, & L. C. Wilkinson (Eds.), Language, literacy, and learning in the STEM disciplines: Language counts for English learners (pp. 13–34). Routledge Taylor Francis.
Naresh, N., Harper, S., Keiser, M., & Krumpe, N. (2014). Probability explorations in a multicultural context. Journal of Mathematics Teacher Education, 108(3), 184–192. https://doi.org/10.5951/mathteacher.108.3.0184
New Zealand Immigration. (2018). Statistics arrivals. https://www.immigration.govt.nz/documents/statistics/statistics-arrivals-bymonth.pdf
Nilsson, P. (2013). Experimentation in probability teaching and learning. In E. J. Chernoff & B. S. Sriraman (Eds.), Probabilistic thinking: Presenting plural perspectives (pp. 509–532). Springer.
Planas, N., & Setati-Phakeng, M. (2014). On the process of gaining language as resource in mathematics education. ZDM Mathematics Education, 46, 883–893. https://doi.org/10.1007/s11858-014-0610-2
Reynolds, M. (2022). A relational approach to learning environments: Learning from Pacific wisdom. New Zealand Journal of Educational Studies, 57, 143–158. https://doi.org/10.1007/s40841-021-00236-x
Robertson, S. A., & Graven, M. (2020). Language as an including or excluding factor in mathematics teaching and learning. Mathematics Education Research Journal, 32, 77–101. https://doi.org/10.1007/s13394-019-00302-0
Saunders, K., Averill, R., & McRae, H. (2018). “I can’t wait to get to maths”: Ako in mathematics teaching and learning. Set: Research Information for Teachers, (1), 11–18. https://doi.org/10.18296/set.0097
Sharma, S. (2014). Influence of culture on high school students’ understanding of statistics: A Fijian perspective. Statistics Education Research Journal, 13(2), 104–117. https://doi.org/10.52041/serj.v13i2.284
Sharma, S. (2018). Bridging language barriers in statistics for Year-12 Pasifika students: A collaborative study. Waikato Journal of Education, 23(1), 107–120. https://doi.org/10.15663/wje.v23i1.646
Sharma, S., Doyle, P., Shandil, V., & Talakia’atu, S. (2011). Developing statistical literacy with Year 9 students. Set: Research Information for Teachers, (1), 43–60. https://doi.org/10.18296/set.0398
Shaughnessy, J. M. (2014). Teachers as key stakeholders in research in statistics education. In K. Makar, B. de Sousa, & R. Gould (Eds.), Sustainability in statistics education. International Association for Statistical Education. https://iase-web.org/icots/9/ proceedings/pdfs/ICOTS9_2G4_SHAUGHNESSY.pdf?1405041595
Spoonley, P., & Bedford, R. (2012). Welcome to our world?: Immigration and the reshaping of New Zealand. Dunmore Publishing.
Sullivan, P. (2020). Is the last banana game fair? Mathematics Teacher: Learning and Teaching PK–12, 113(1), 33–38. https://doi. org/10.5951/MTLT.2019.0131
Tai, K. W. H. (2021). Translanguaging as inclusive pedagogical practices in English-medium instruction science and mathematics classrooms for linguistically and culturally diverse students. Research in Science Education, 52, 975–1012. https://doi. org/10.1007/s11165-021-10018-6
Trinick, T., Meaney, T., & Fairhall, U. (2016). The relationship between language, culture and mathematics. Journal of Mathematics and Culture, 10(2), 175–191.
Vaioleti, T. (2013). Talanoa: Differentiating the talanoa research methodology from phenomenology, narrative, kaupapa Māori and feminist methodologies. Te Reo, 56/57, 191–212.
Watson, J., Fitzallen, N., Fielding-Wells, J., & Madden, S. (2018). The practice of statistics. In D. Ben Zvi, J. Garfield, & K. Makar (Eds.), International handbook of research in statistics education (pp. 105–137). Springer. https://doi.org/10.1007/978-3-319-66195-7_4
Join the
TLRI mailing list
Confirm what happens to email addresses submitted? ie processes around the TLRI email subscriber list
Recently Completed
Project Categories
Can we discuss navigation by Categories at our next meeting. Only 5 projects have been put into sub-categories (Maths and Assessment) above. It would be useful to have feedback as to whether it’s worth creating and assigning sub-categories for all the projects

