Te reo tataitai: Developing rich mathematical language in Māori immersion classrooms

1. Aims, objectives, and research questions

Kō ta te rangatira kai he kōrero

As described in the whakatauaki (proverb) above, language is the food of chiefs because fluency in it provides access to and control of learning. Khisty and Chval (2002) summarised the effect of this by stating, “[i]n essence, those with power are literate or in control of a discourse” (p. 167). Although Māori students who attend Māori immersion programmes do better than those attending mainstream schooling, generally they do not perform as well as other students in mathematics (Anthony & Walshaw, 2006 forthcoming). One of the reasons for this may be the difficulties Māori students have with the mathematics register. Yet, mathematics is often considered a gatekeeper subject in which students need to do well in order to gain high-earning positions (Nelson-Barber & Estrin, 1995). Analysis of the Māori medium numeracy project (Te Poutama Tau) student data found that language proficiency was a significant factor in student achievement in the higher stages of the number framework (Christensen, 2003). Better understanding of how the mathematics register is acquired is likely to be of benefit not just to kura kaupapa teachers and their students but to others considering language issues in other content areas.

Being fluent in the mathematics register allows students to participate more effectively in mathematical activities. The mathematics register consists of the vocabulary and grammatical expressions that occur frequently when mathematics is discussed (Meaney, 2005). Burton and Morgan (2000) stated that “[t]he language used in mathematical practices, both in and out of school, shapes the ways of being a mathematician and the conceptions of the nature of mathematical knowgledge and learning that are possible within those practices” (p. 445).

This project provides information on the acquisition of the mathematics register by documenting and evaluating the scaffolding and modelling of students’ mathematical language by the teachers in a kura kaupapa Māori. Having the whole kura involved in this project meant that the results are seen as coherent by teachers and of use in discussions about the mathematics programme. The final stage of the research investigated how this knowledge affected the teaching practice of those involved and this enabled an appropriate evaluation of the research for its practical value to be carried out.

The interaction between language and mathematics learning

Although the importance of language in mathematics learning has been well known for a number of years, how the mathematics register is acquired is still poorly understood (Meaney, 2004). In Māori medium classrooms, the situation is further complicated by the newness of some of the mathematics language (see Christensen, 2003; Meaney, Fairhall, & Trinick, 2006). As with other indigenous languages, the development of a mathematical register in te reo Māori has implications for the language as a whole (Roberts, 1998; Barton & Fairhall, 1995; Barton, Fairhall, & Trinick, 1998). Christensen (2003) reported that many teachers were following the English grammatical structure when describing an addition problem such as 3 + 2 = 5. Traditionally, te reo Māori would express this type of construction with the verb stated first (and in the passive case). There was concern that the imported grammatical structure from English could be transferred to other discussions in te reo Māori and, therefore, have a major effect on how ideas could be expressed. In the research carried out at this kura in 1998–1999, there had been a recognition in discussions between the parents and the teachers of that time about the effect of teaching mathematics in te reo Māori (Meaney, 2001). It was agreed that the teaching of mathematics through te reo Māori needed to be done in a way that minimised damage to the language.

We’ve talked about how to use the language of addition and subtraction and tried to come up with something that’s going to enhance Māori instead of around the other way but you know in Te Aho Matua [the philosophy document], they talk about the quality of te reo. (Meaney, 2001, p. 9)

Gibbs and Orton (1994) stated that although mathematical registers can be developed in indigenous languages, they need to be used by people to be effective, and research needs to be done on “the stage in conceptual development when specific mathematical vocabulary items are helpful [and] how they should be introduced” (p. 100). Certainly, reports such as those of Christensen, Trinick, and Keegan (2003) and Christensen (2003) raise issues in regard to the use of te reo Māori in the teaching of mathematics. The first report comments on current inconsistencies in mathematical expressions used by teachers in Māori medium classrooms. The second report highlights the need for language proficiency in the implementation of Te Poutama Tau, the numeracy project equivalent for Māori medium situations. Three of their 11 key findings related to language. These were:

• Language proficiency is a significant factor that impacts on students’ progress in the higher stages of the Number Framework. However, students with lower levels of proficiency did not seem to be disadvantaged at the earlier stages of the Framework
• Teachers were generally concerned to ensure that their use of language in the pāngarau lesson was correct, concise and clear. However, in many cases “local” vocabulary for mathematical concepts was favoured ahead of standardised terms and the rationale for having standardised terms was not well understood
• The programme was seen to make high demands on teachers’ and students’ language use and in some cases language proficiency was identified as an impediment to students’ achievement. (Christensen, 2003, p. 8)

Issues of language proficiency for indigenous students learning mathematics is not isolated to Māori in New Zealand, but has been noted in regard to Hawai’ian students (Brenner, 1985), Aboriginal students (Graham, 1988), and students from Botswana (Berry, 1985). In Māori medium classrooms, this situation is further complicated because not all children have te reo Māori as their first language and so are learning the language as they learn the content.

The role of the teacher has been emphasised in providing the environment in which learning should occur (Anghileri, 2002). This learning includes expectations about the interpretation and production of mathematical language (Khisty & Chval, 2002). Khisty and Chval (2002) showed the importance of the teacher’s own use of mathematical language when students were learning in a second language. When teachers do not use mathematical language fluently, their students are unable to describe the mathematical ideas that they are learning.

The two main ways that support is provided to students to learn and use the mathematics register are modelling and scaffolding. Modelling is when a teacher uses mathematical language within an appropriate context. For example, if a student provides a response to a mathematical task in everyday language, a teacher might rephrase it in more appropriate mathematical language (see Chapman, 1997).

Scaffolding is when a teacher provides part of a response, with the student completing the rest. Wood, Bruner, and Ross (1976) originally described the scaffolding by an adult as that which “enables a child or novice to solve a problem, carry out a task or achieve a goal which would be beyond his unassisted efforts” (p. 90). Williams and Baxter (1996), in looking at scaffolding in a mathematics classroom, distinguished “analytical scaffolding, the scaffolding of mathematical ideas for students, from social scaffolding, the scaffolding of norms for social behaviour and expectations regarding discourse” (italics in original, p. 24). In discussing the social scaffolding that they saw, Williams and Baxter (1996) believed that “[the teacher] wanted [the student] to know why talking about mathematical ideas was important” (p. 29). Although the distinction between analytical and social scaffolding is not always clear, the research carried out in this project can be considered to be predominantly about social scaffolding.

As time goes on, a teacher would expect to reduce the amount of scaffolding and modelling that they provide, thus transferring the responsibility for using the language from the teacher to the student. Siemon and Virgona (2003) suggested that this transfer of responsibility for learning can be related to Vygotsky’s Zone of Proximal Development (ZPD).

Students who are most dependent on teacher support might be expected to be working at the margin of their ZPD, requiring the teacher to model, prompt, demonstrate or coach, in order to come to new understandings and insights. Students who are least dependent on teacher support might be expected to be operating well within their ZPD, requiring little or no intervention from the teacher, and accessing a range of appropriate metacognitive strategies to monitor their own learning. In this case, a different set of teacher actions might be invoked, for example, reflecting, celebrating, inviting and listening. (p. 2)

However, as Williams and Baxter (1996) stated, there is a risk that this transfer of responsibility fails to occur in many classrooms: “Edwards and Mercer pointed out that handover, or the process of gradually shifting control of learning from teacher to student, was missing in the classrooms they observed” (p. 25).

Although the work of Bickmore-Brand and Gawned (1990) would suggest that the effect of modelling and scaffolding of mathematical language has been known for some time, there has been limited research on what are effective modelling and scaffolding strategies. Chapman’s (1997) study would be the most comprehensive. From watching a secondary mathematics class for a term, Chapman described how teachers reframed student responses so that they clearly showed the relationship to the theme of the lesson; focused on the typical linear, metonymic structure rather than the metaphorical content; and became more certain and less hesitant (what she labelled as high modality). Although Chapman concentrated on the teacher’s role within the interactions, researchers such as Rogoff (1988) showed that students themselves have a major influence on the types of scaffolding and modelling which are offered to them.

There is also cross-cultural research on mother–child interactions which suggests that the ways that scaffolding are carried out are culturally determined (Kermani & Brenner, 1996). Research in reading classrooms for Hawai’ian students suggested that reading achievement increased when discourse interaction patterns more closely matched those of a traditional Hawai’ian cultural activity, such as talk story (Au, 1980). Therefore, Māori teachers teaching Māori children in te reo Māori may not use scaffolding strategies similar to those identified by Chapman (2003). NelsonBarber and Estrin (1995) suggested that “[u]nfortunately much of the knowledge on culturally influenced notions of good teaching remains unrecorded and unformalized because, as a whole, educators (researchers and practitioners alike) have made little effort to elicit the perspectives and experiences, or study the classrooms, of teachers who are highly effective with non-mainstream students” (p. 5). This research, based on the questions that teachers had about their own teaching, would also help others working in similar situations.

Research questions

As a result of this acknowledgement of the importance of language in mathematics learning, the teachers at Te Kura o Te Koutu wanted to know more about how students acquired the mathematics register. The teachers in the primary section of the school were also participating in Te Poutama Tau, and felt that this research would complement that project. In this Teaching and Learning Research Initiative-funded study, teachers investigated how they modelled and scaffolded mathematical language. From their findings, there was a need to develop a coherent understanding of how the modelling and scaffolding strategies changed across the classes from Year 0 to Year 13. This knowledge could then be used to enhance students’ use of language in their mathematics learning.

The aim of the research was to develop a school-wide understanding of how mathematical language is modelled and scaffolded and how these strategies needed to change as students progress through the school. As a consequence, the research questions were:

• What are the most effective ways for teachers to model and scaffold mathematical language for students?
• Are these modelling and scaffolding strategies different for different ages of students?
• Does awareness of different modelling and scaffolding strategies have an effect on the ways that teachers approach the development of students’ mathematical language?

2. Research design and methodologies employed

This research involved evaluating effective mathematical language modelling and scaffolding strategies, and so there was a need to identify an appropriate research methodology. The project was also occurring in a kura kaupapa Māori and therefore there was a need to honour this context and the culture of the participants. The methodology had to provide rich data but also support teachers to be both participants and researchers in close collaboration with the other researchers at specific times. Consequently, the project was modified as the role of scaffolding and modelling became better understood, and this contributed to the teachers becoming more reflective researchers of their own teaching practices.

Brenner (1998), using the work of Eisenhart (1988), suggested that research into improving mathematics instruction for culturally diverse groups of students can be seen as fitting into two different research paradigms. These are the ethnographic research tradition and the mathematics education tradition. The first paradigm uses tools from anthropology to better understand the students and their backgrounds and to try to close the gap between home and school. The latter research paradigm, from a cognitive science base, investigates how an individual student is able to grapple with mathematics.

There were two reasons for deciding to use the ethnographic research tradition. The first is that research in kura kaupapa Māori needs to be in alignment with kaupapa Māori or Māori-centred research tradition. The second is that, as the project was about evaluating the effectiveness of different modelling and scaffolding strategies, an ethnographic research tradition provides better support for this than the mathematics education tradition.

Dimensions of kaupapa Māori research

Christensen (2003) summarised the five dimensions that contribute to kaupapa Māori research. Each of these dimensions is described in the following paragraphs, with an indication of how they were met in this project.

A Māori world view

There is a need for the unique Māori world view to be reflected in what is researched, how it is analysed and written up. In considering how te reo tātaitai (the mathematics register) is scaffolded, there is a need to be aware of those strategies that are unique to the language and culture of the teachers and the students. If Māori students are to improve their educational achievement, the role of culture in learning needs to be acknowledged. It cannot be assumed that good teaching for students from diverse backgrounds will always look the same (Alton-Lee, 2005). It is, therefore, important that effective practices that resonate with cultural practices are documented, and this was one of our aims for this project.

Culturally safe research practices

There is a need for Māori to feel that they will not be exploited as a consequence of being involved in research. Irwin (1994, cited in Christensen, 2003) suggested “mentoring by kaumātua and research being undertaken by a Māori researcher as two aspects of culturally safe practices” (p. 14). In our project, two of the principal researchers are respected Māori mathematics educators. Their involvement has provided a mentoring role for the teachers who were involved in researching their own practices. Regular meetings with teachers meant that the project could evolve to meet the needs of the kura as the teachers’ opinions and ideas were incorporated into what was being researched and how this was being done.

Challenges to existing power relationships

It is important that kaupapa Māori research results in Māori development. In order to do this, the way that Māori have traditionally been portrayed needs to be reconsidered. This will support students’ active movement into the wider society as the primary benefactors from the research. By documenting effective strategies and acknowledging their relationship to culture, we anticipate that the effect of this research will not just support students at this kura, but be of value to students at other kura.

Accountability and mediation

There is a need to ensure that control of the research remains with Māori so that “the research is worthwhile and contributes to Māori development” (Christensen, 2003, p. 15). This will ensure continued validation of the research so that it reflects a Māori world view and culturally safe research practices. In our research, we did not have a supervisory group. However, the project was jointly run by the researchers, two of whom were Māori, with frequent meetings with the teachers who were also researchers of their own practice. As a group research project, there were opportunities for reassessment as it progressed. The project, therefore, was accountable to the people who were involved in it.

The researcher is concerned with Māori advancement

The positioning of the researcher is important in kaupapa Māori in order for the different issues of doing research, such as the need for Māori development, ethics, and being systematic, to be considered. This research was a joint activity which valued the different skills and experiences brought to the research project. This ensured that the various demands of the research were dealt with adequately. All of those involved in the project are concerned with Māori advancement.

Ethnographic research tradition

Fetterman (1993) provided the following description of the ethnographic research tradition and its relationship to educational evaluation:

Key elements of this approach involve conducting fieldwork and maintaining a cultural perspective. Concepts that guide this effort involve maintaining a holistic and contextual perspective, eliciting the emic or insider’s perspective about their reality and adopting a nonjudgemental attitude. Additional ethnographic tools include key informant interviewing; informal, semistructured interviewing; and triangulation. These methods and concepts, traditionally used to understand sociocultural systems, are applied to educational evaluation in an attempt to assess more accurately the relative merits of a given educational approach, setting or system. (p. 2)

To this research methodology, there was also a need to include elements of participatory research as the teachers were both the subjects of the research and also the researchers. As joint researchers, we were “co-creating reality through participation: through experience, imagination and intuition, thinking and action” (Reason, 1994, p. 324). Complementary accounts methodology combines aspects of educational ethnographic research and participatory research and seemed to suit our needs. It had been developed by Clarke (2001) and his colleagues for studying “learning in legitimate classroom settings, whilst minimizing researcher inference regarding participants’ thought processes and maximizing the richness of the research database” (p. 13). Clarke identified the following features as being integral to this research approach:

• The nature of the data collection procedure, leading to the construction of “integrated data sets” combining videotape and interview data
• The inclusion of the reflective voice of participant students and teachers in the data set
• An analytical approach that utilises a research team with complementary but diverse areas of expertise to carry out a multi-faceted analysis of a common body of classroom data. (2001, p. 14)

Clarke’s (2001) research project investigated the learning process, whereas our project looked at the modelling and scaffolding of mathematical language. By videotaping classrooms and involving teachers as researchers, we could combine the classroom data with teacher insights so that we had an integrated data set. Surveys at various times during the project also provided us with teachers’ reflections on their own practices. Although we had hoped to interview some students about their experiences and, thus, add to our data source, this did not occur except in a haphazard manner. Our problems in this area are described in more detail in the next section. We were also interested in discovering the effect that participating in the research had on teachers’ own practices. It was, therefore, inevitable that the methodology needed to be adapted as the project progressed. The changes are documented below.

Participants and method

Kura Kaupapa Māori o te Koutu is in a mid-sized rural town in New Zealand. In kura kaupapa Māori, “the pedagogy of these schools is based on, but not exclusively, Māori preferred teaching and learning methods” (Smith, 1990, pp. 147–148).

The parents place their children in the kura so that they learn in Māori, although the parents themselves may not be fluent Māori speakers. Most students, therefore, acquired Māori as their second language, predominantly in the various school domains. These students have been described as having “elective bilingualism” (McNaughton, MacDonald, Barber, Farry, & Woodard, 2006, p. 3). As described by McNaughton et al. (2006), this type of bilingualism is likely to result in classrooms that contain students with different commands of oral and literacy skills in te reo Māori and English. These differences will affect learning.

As well as having students with different degrees of fluency in the classroom, the teachers also had different experiences with the mathematics register in te reo Māori (te reo tātaitai). Very few teachers learnt mathematics in te reo Māori and so many were learning the mathematical terms in Māori at the same time as they were teaching the concepts to the students. Teachers in the earlier grades were also unlikely to know the mathematical terms that their students would need in the following years of schooling. It was the realisation that these issues would have an effect on their teaching that resulted in the teachers wishing to participate in this project.

By the end of 2005, one teacher who had agreed to participate in 2004 was no longer teaching mathematics, and two new teachers had started in the third term. The participants’ teaching experience ranged from being in the first weeks of their first appointment to having 20 years of teaching mathematics in te reo Māori. In 2005, mathematics was taught by seven teachers, who were split into two pairs and one group of three. Several of the teachers taught multiple classes of mathematics. Each of these teachers chose one class to be their focus for the project. One term was associated with each group. The teachers of the senior classes, including the high school and intermediate classes, videotaped their lessons in Term 2. Junior primary classes were videotaped during Term 3. The remaining classes were videotaped in Term 4.

Ethics approval was sought and gained from the University of Otago Ethics Committee. However, concerns were raised about filming in classrooms where not all students had agreed to be participants. The Ethics Committee initially suggested that filming should not occur if one student did not agree to participate. As this may have meant that filming would not have occurred in several classrooms, a compromise was reached that if students or their parents did not consent to the videotaping, the students would sit outside the camera’s range and none of their contributions would be used. A meeting was held with parents early in 2005 where the project was explained and permission sought for the filming. Consent forms were also sent home to parents who had not been able to attend the meeting. If classroom videotape extracts are to be shown when presenting the findings of this project to outside groups, permission will be sought again from students and their parents. In the end, only one student declined to be a participant and she was seated outside the camera range for the two lessons that she attended.

Originally, it was hoped that each teacher would record a series of five lessons. By having the teachers record five lessons with the same class, it had been anticipated that we would be able to see students using the new words in the later lessons. Gibbons (1998) had been able to identify how students’ everyday language had changed to incorporate the features of the scientific register from videotaping lessons and collecting students’ writing. We had also hoped that a set of five lessons would allow us to gain a sense of the language learning that students achieved in the course of a week. However, only one teacher recorded all five lessons for analysis. The junior classes often worked with different groups over the course of a week and so we did not always see them working with the same group on the videotapes. As well, difficulties with having a camera person meant that most teachers only had two or three lessons recorded. The ad hoc nature of the lessons that were videotaped meant that we were unable to see students fluently use new aspects of the mathematics register. However, given that we already struggled with the amount of data that we had collected, it is unlikely that we would have been able to analyse students’ use of the mathematics register across the series of five lessons without significantly more funding.

When the project was set up, we had anticipated using two cameras to do the filming. One camera would be trained on the front of the classroom and would capture the teacher’s conversation and what was written on the board. The other camera, at the front of the classroom, would be trained on the students and would capture the students’ contributions. In Clarke’s (2001) research, equipment enabled the two videotapes to be integrated into one image. We did not have this facility, but were able to edit the videotapes so that the most appropriate image could be seen on the merged video. However, only the senior classrooms were videotaped in this way. The primary teachers tended to work on the floor either with the whole class or a small group, and having two cameras operating was not practical. There were also significant difficulties in capturing the students’ talking clearly when there was considerable background noise.

Like Clarke, we also interviewed students about their use of language. Originally it had been hoped to gain students’ opinions of the interactions captured in the videotapes. However, the logistics of trying to organise this meant that it was not achieved in the first year of the project. Instead, senior students were asked about their use of language in external mathematics examinations. The examinations for the National Certificate in Educational Achievement are written in both Māori and English. Very few people teach mathematics in the final years of high school in te reo Māori. Consequently, there can be variation in mathematics vocabulary (see Meaney, Fairhall, &Trinick, 2006) and, therefore, the English version can be used by students to check their understanding of some Māori terms. As these data are not directly related to the research questions for this study, they will not be included in this report but will be reported elsewhere. In 2006, some students were interviewed about situations that arose in the classroom videotapes. These interviews were exploratory and have not been analysed. What we have learnt from doing these videotapes will enable us to do this procedure more successfully in our 2007 research project on writing in mathematics classrooms.

The research team consisted of the teachers, including the teaching principal, and two universityresearchers. Clarke’s (2001) team was much larger but did not include the teachers whose lessons were being analysed. As this project was designed to work on a school issue, it was important that the teachers were actively involved as researchers.

After watching the videotapes, the teachers were to choose snippets from the lessons which focused on language. Some teachers did this while other teachers allowed their lessons to be analysed. The videotapes were then put onto a CD and sent to a transcriber. The videotapes and transcriptions were analysed by the teachers with the support of the researchers.

The analysis was done using the Mathematics Register Acquisition model (Meaney, 2006a). This model is given in Figure 1. It makes links between the acquisition of a second language and the acquisition of a subject register in a first language. The model was in its developmental stage during the research. It supported teachers to consider the strategies they used without feeling they were comparing themselves against a norm of acceptable practice. The model should not be seen as the only way that the acquisition of mathematical language can be envisaged. The teacher and a researcher would watch the videotapes, referring to the transcripts where necessary. They decided what the language focus of an interaction was and the stage of the model where the interaction could be located.

As shown in Figure 1, this model has four stages. First, students have to notice that there is new language to be learnt and when it is used by others. With prompting by others, students will use the new terms and expressions. Gradually the prompting is lessened and students start using the terms in a variety of situations. Feedback, both positive and negative, helps them to refine their understanding of when and how to use the terms and expressions. After students have consolidated their understanding, the terms and expressions will be integrated into their linguistic repertoire. Students will use these terms consistently except when the situation is challenging and they may revert back to simpler terms. The final phase is when students are using the terms fluently even in the most demanding situations.

Figure 1 Model of Mathematics Register Acquisition

If mathematics lessons are considered language learning experiences, then it is possible to categorise the interactions according to the different stages of the model. The first step is to identify the key linguistic terms or expressions within an interaction. This interaction may last for only two turns or for a large part of a lesson. By looking at who uses the terms or expressions and in what ways, it is possible to link the interaction to a stage in the Mathematics Register Acquisition model. It is also important to identify the language skill—reading, writing, listening, speaking—that the student is using. Language acquisition requires students to interpret, through listening and reading, as well as to produce new language, through writing and speaking. There is also a need to document what the teacher and student do to initiate or support the continuation of the modelling and scaffolding strategies being used.

The analysis of all the teachers’ lessons was documented. This has allowed us to compare different strategies. Teachers were then encouraged to try out strategies that they had not previously used. This led to discussions about what constitutes an effective strategy and whether use of these strategies was affected by the age of the child or teaching style of the teacher. Using concepts about triangles, the teachers also had a discussion about the mathematics register that they expected students to be able to use fluently when they arrived at the different year levels and the language that they would teach at that year level. The results of this discussion are described in Chapter 4.

One of the researchers, Tony Trinick, has begun an investigation into the use of logical connectives in te reo tātaitai by both teachers and students. In the mathematics register, these words or phrases connect different ideas together in a logical sequence (Meaney, 2005). Te reo Māori has an abundance of these logical connectives, and how they are used in mathematics classrooms has implications for the cultural teaching in the classroom. However, as this was not a focus for this research, the results will be not be included in this report but will be published separately.

The teachers also completed surveys twice during the course of the project. The first survey asked teachers about possible ethnomathematics practices that they could use in their classrooms and what they felt the possible language implications might be in using these. The results of this survey are reported in Meaney, Fairhall, and Trinick (2006) and are not repeated here, as the results do not have a direct effect on this research.

In 2006, teachers were again videotaped and these videotapes discussed. This provided some data for the teachers to use to reflect on how their practices had changed as a result of participating in the project. The second survey was completed in Term 3 of 2006 and asked teachers to reflect on their participation in the project. Teachers were also interviewed at the same time about their experiences. This data was used in answering the third research question and is reported on in Chapter 5. A copy of the questionnaire is provided in Appendix A.

In the surveys and the interviews, teachers talked about being more aware of their use of the mathematical register in their own teaching. The need for students to know and use the specialist vocabulary of te reo tātaitai has been raised in a number of reports (Christensen, 2003; Christensen, Trinick, & Keegan, 2003). It was, therefore, felt that it would be useful to see whether a raised awareness of this issue had an effect on teachers’ practice. We felt that we would expect to see a greater number of mathematical words than nonmathematical words used repeatedly in the 2006 videotaped lessons than we had in the 2005 videotaped lessons. Consequently, the use of mathematical vocabulary was counted and compared with the use of other words in both the teacher and the students’ contributions in the videotaped lessons in 2005 and 2006.

McNaughton et al. (2006) had counted the occurrence of various words in literacy lessons in Māori medium classrooms. Thornbury (2002, cited in McNaughton et al., 2006) suggested that effective learning of vocabulary by second language learners requires: the repetition of the terms at least seven times; retrieval; spaced opportunities to use the vocabulary; and purposeful use of the new vocabulary. Given that the mathematics lessons were varied in the content covered, the newness of the topic, and the length of the lessons, it was unlikely that counts of total numbers of words spoken would allow any meaningful comparisons to be made. It was, therefore, decided to identify the number of words that were used more than seven times in each mathematics lesson.

The words were then categorised as either being part of the mathematics register or words that fulfilled other classroom functions such as behaviour management. Total counts were made of the number of times the words were used by the teacher, the number of times the words were used by the students, and the total number of times the words were used. Each teacher’s sets of lessons were compared for the use of common words in 2005 and in 2006.

The methodology for this project needed to be flexible so that the research could be adapted to suit the ongoing needs of the teachers. There was also a need to gain as rich a data set as possible. As a result, data were collected through videotaped mathematics lessons, surveys, and interviews. The teachers were involved in the data gathering and the analysis of their own modelling and scaffolding of the mathematical register. Analysis was also carried out on the effect that being involved in the project had on teachers’ understandings about the acquisition of the mathematics register and their classroom practices.

3. Scaffolding and modelling of te reo tātaitai

The first research question was: What are the most effective ways for teachers to model and scaffold mathematical language for students? In order to investigate this, videotapes were made of all the teachers. At least two videotapes were recorded for each teacher. In the junior classes, the teachers tended to take small groups rather than work at the whole-class level. This resulted in a lot of background noise, making the videotapes difficult to transcribe. Consequently, recordings done in Term 4 had the teacher take a group in a separate room while the rest of the class was looked after by another teacher.

The 2005 videotapes were analysed by a university-researcher with the teacher whose lessons were videotaped. Although it had been anticipated that the videotapes would be analysed as soon as possible after they had been made, this did not eventuate. The major difficulty was that the transcribing was difficult to organise. This did affect the usefulness to the teachers of doing the analysis, and in subsequent research, delayed analysis will be avoided as far as possible. However, all the teachers found the analysis beneficial. This is described in Chapter 5 on the teachers’ perceptions of the research.

From this analysis, a description of all of the scaffolding and modelling strategies was made, categorised, and written up according to the four stages of the Mathematics Register Acquisition model. This included an indication of the roles of the teacher and the students in initiating and maintaining the interaction. An example of these notes can be seen in Appendix B.

Strategies for each stage

Below is a summary of the strategies used in relation to each stage of the model. The sections that follow expand upon the descriptions of the strategies for each stage, giving an example from the transcripts.

Noticing

Strategies identified with the noticing stage were:

• providing opportunity for the new terms to be used appropriately
• using linguistic markers to highlight what is to come
• using intonation to emphasise a correct term after students use an incorrect one
• repeating new terms and expressions several times in appropriate places
• rephrasing the expressions by using other terms
• writing the new term in an equation which is related to what had just been discussed
• giving definitions verbally and through diagrams
• emphasising the relationship between ideas using diagrams or physical materials and words
• modelling a new term, skill, or idea as it is being explained
• after teacher explanation, having students say back the new term
• having students repeat the final answer after the teacher has modelled finding the solution
• relating new terms to already known ones
• using a set of leading questions so that students are channelled into using a particular term
• using “fill-in-the-blank” sentences
• acknowledging the difficulty of learning some terms or ideas
• providing a rationale for the need to learn a new term or idea
• requesting students’ attention before introducing a new term
• describing a new term as being important in a subsequent lesson.

Intake

Strategies associated with the intake stage were:

• having choral responses with the students
• having students as a group do choral responses
• giving the first syllable of a term so that students are reminded of the term and then complete it
• asking students for names, definitions, or explanations of terms
• having students model the use of terms, skills, or ideas
• asking students for examples of a term
• using the similarities between concepts (e.g., 7 + 3 and 70 + 30) as an entry into having students reflect on the differences
• having students draw their own diagrams or use materials to show a particular term
• repeating or having students repeat appropriate responses
• elaborating on students’ responses in words and with diagrams
• asking further questions to help students reflect on what they are describing and to check on what they know or have done
• having students provide a rationale for what they are learning
• ignoring inappropriate answers and just acknowledging appropriate ones
• querying students’ inappropriate responses
• suggesting that students’ inappropriate responses are close
• having students work backwards from an inappropriate answer to the question which was asked
• using specific amounts to illustrate a general rule or idea
• focusing students back on to the main idea being discussed to help solve a problem
• using student-devised terms in giving an explanation
• going over an activity which requires the use of the new language as a whole class before expecting students to do the activity as individuals
• showing students the relationship between what they already know and can do and the new language term or skill
• having students answer a series of closed questions to lead them to using the new term, skill, or idea
• after modelling how a new term or skill is used, having students repeat the action
• recording in writing what has been discussed or done
• having students query obvious errors by the teacher or another student.

Integration

Strategies associated with the integration stage were:

• using commands and linguistic markers to highlight for listeners that they need to pay extra attention to what they are hearing and doing
• encouraging students to make contributions to the teacher and to each other
• reminding students to think about what they already know
• asking a student to repeat a good response
• if a slight correction is needed, the teacher repeats the response correctly
• summarising what a student has said
• if a slight correction is needed, the teacher can model doing the action so that the student selfcorrects their own response
• prompting in a general way for more details
• having students write a summary of, or record as a diagram, what they have learnt
• facilitating an environment where students will correct each other
• asking students to say whether an answer or term is correct
• repeating the question if the students appear to have responded to a different one
• having students complete appropriate actions as they respond to questions.

Output

Strategies associated with the output stage were:

• providing opportunities for students to use their acquired aspects of the mathematics register between themselves and with the teacher
• providing an environment in which the students can query the language use of the teacher.

In the following sections, the teachers are individually labelled (T1, T2, T3, T4, T5, T6, and T7). The extracts have been tidied so that some of the disjointed nature of oral communication has been smoothed, but the substance has not been changed. Empty brackets in the transcripts indicate where a word was inaudible. As the data came from videotapes and, thus, had visual images as well as the transcripts, it was decided not to translate the te reo Māori into English. Instead, a description of each incident is provided below that uses information both from the extracts and from the visual images.

Noticing

These strategies were used by teachers to make students aware of new vocabulary or grammatical expressions of the mathematics register. Mathematics tends to layer terms and expressions with meanings, so often teachers were drawing students’ attention to these added layers rather than introducing new terms and expressions.

At this stage of learning, most of the responsibility for highlighting new language is with the teacher. Otterburn and Nicholson (1976) investigated students’ understanding of terms commonly used by their teachers and found that a number of students had little, if any, understanding of their meaning. When students did have a meaning for a term, it was often not the same as their teacher’s. The importance of this stage should not be underestimated. Students need to recognise that a new term or expression is important before they can begin to learn it.

Providing opportunity for the new terms to be used appropriately
One of the junior teachers used the story of Little Red Riding Hood to introduce the term tērā pea (perhaps) as part of a series of lessons on probability.

	T4:	He aha i roto i te ngahere?
	Ākonga 1:	He kau.
	T4:	He kau i roto i te ngāhere [boy laughs], tērā pea. Ākonga 2, i kite ia i te aha?
	Ākonga 2:	He wūruhi.
	T4:	He wūruhi, āe. Kua kite kē ia i te wūruhi. [Nods to another child] Kua wareware, he aha ngā momo mea ka kite a Pōtae Whero i roto i te ngāhere?
	Ākonga 3:	He kiwi.
	T4:	He kiwi, āe, tērā pea.
	Ākonga 4:	He manu.
	T4:	He manu, āe. He manu i roto i te ngāhere. He whakaaro anō?
	Ākonga 5:	Ka kite i te whare.
	T4:	He whare, āe, tērā pea, ka kite ia i tētahi whare. He whakaaro anō? Marama, Ākonga 1. Āta whakaaro ki te ngāhere i kitea e ia.

The teacher used a familiar story to build on students’ probability vocabulary. The students already had ideas about the certainty of an event occurring or not occurring. By repeating tērā pea, the teacher was highlighting both the concept of uncertainty and the word that describes it. The context meant that the students had an active part in the lesson, but the teacher could be sure that she would be able to introduce the new vocabulary.

Using linguistic markers to highlight what was to come
Te reo Māori has a number of linguistic markers that can be used to highlight information for listeners. One teacher in particular was very good at making use of these words so that students would be forewarned about the type of information they were to receive. Kē is one of these words as it tells the listener that what is to follow is unexpected. Another is arā.

T1:

Ānei tētahi o ngā ahutoru, arā, te koeko tapa whā, mahara?

This utterance began the first of this teacher’s videotaped lessons and referred to material covered in the previous lesson. The teacher highlighted one term ahutoru (pyramid) as the word which needed to be recognised and understood. She did this by using arā to mark that a definition was coming. Although the term was used in a previous lesson, the teacher assumed that many of the students were still in the first stage of the model and their attention needed to be drawn to ahutoru.

Using intonation to emphasise the correct term after students have used an incorrect one
Rather than providing students with direct feedback about the use of the mathematics register, many of the teachers used the tone of voice in repeating an answer to provide indirect feedback.

	T2:	I haere a Ākonga 1, ki te whare kararehe ki te tirotiro ki ngā makimaki. I kite a Ākonga 1 e rima ngā makimaki nui. Whakaatu mai ki a mātua. Tuatahi, mā ngā pātene, e hia ngā makimaki nui? [Students take buttons] Ā i kite hoki ia e toru ngā makimaki paku. Whakaatu mai e toru ngā makimaki paku. Nō reira, i runga i tēnā e hia katoa ngā makimaki.
	Ākonga:	Waru.
	Ākonga:	Waru.
	T2:	E hia katoa?
	Ākonga:	Waru.
	T2:	E waru ngā makimaki, ka pai.

In this example, the teacher asked the child how many monkeys there were altogether. Two students responded waru. The teacher then asked another student to respond, but emphasised the e in the question. He then also replied waru. The teacher repeated the answer as e waru with the emphasis on e.

Repeating new terms and expressions several times in appropriate places
Quite often when a new term was being introduced, the teacher repeated it many times, often associating it with activities. In one of T6’s lessons on introducing division, she used whakawehe (division) 41 times and the students used it 10 times. These repetitions were spaced, giving students time to absorb the vocabulary. Spacing repetition has been noted as important in vocabulary acquisition in second language learning (McNaughton et al., 2006).

	T6:	Nā ka ono, waru, tekau, i kaute ahau i ngā ( ) ana ( ). E hia ngā mea paraone? E whā ngā rōpū. He rereke, āe. He mahi māmā tēnei. Ko te tumanako, he mahi māmā mā koutou. E whā ngā rōpū taki, ana. E hia ngā tae ia tae. E whā ngā rōpū. Nuku atu i ō koutou pukapuka kia taea e koe te waiho ngā mataono ki mua i a koe, kua pēnei koe.
	Ākonga:	Āe.
	T6:	Kua whakatakoto koe i o mea pēnei [teacher observes students]: Nō reira, titiro mai, he mea kowhai i pērā hoki koe.
	Ākonga:	Kāo.
	T6:	Anā, he aha te pātai mā koutou? I tēnei rā. Kāore au i te hoatu te whakawehe ki a koutou nērā mā koutou. Kia whakaaro, āe, me whakaaro pea e koutou. Mehemea i ahau e rua ngā rōpū takitoru. E hia te katoa o ia takiwha? E hia te katoa o ngā tor- toru?
	Ākonga:	Ono.
	T6:	Ka tahi, rua, toru, whā, ono, ko tēnei te whakarau aha e ono.
	Ākonga:	Toru, toru.
	T6:	Tuhia te whakawehe mōku. E hia te katoa ehara ko te toru [throws pen to child].
	Ākonga:	( )
	T6:	Timata i te aha, ka pai.

In the extract, the teacher had the students separate blocks into groups. This allowed her to introduce the term whakawehe which then became the focus of the lesson.

Rephrasing the expressions by using other terms
Rephrasing students’ utterances so that they become more mathematical is a common strategy used by teachers, not just in this research (Bill, Leer, Reams, & Resnick, 1992; Chapman, 1997). It has the advantage that not only has the teacher highlighted new aspects of the mathematics register, but the language has more chance of being noticed as it relates to what students are trying to describe. In the next example, the teacher was rephrasing a student’s utterance so that it became a more general explanation.

	Ākonga 1:	E rima ki runga, e rima ki raro ka tekau. Ono ki muri e whā ki mua ka tekau tāpiri e whā ki muri me ngā taha, me ngā taha e whā, me kotahi te ( ).
	T1:	Kia ora rawa atu. He pai hoki tō reo ka rongo … he aha tāu? Kia kite atu i pēnei kē nēhā. Ki tōku kei te rongo koe, Ākonga 2 tāpirihia ngā ira kei te noho ki runga nei ki ngā mea i raro. Kāore i te kite, nēhā? Ka tekau nē? Katahi, kī mai ka timata ki ngā ira kei muri rā anō e ono tērā me wēnei, ka tekau. Nā reira e ono i konei. Ka taea e koe te kite ināianei tonu Ākonga 2 me tērā taha. Ko wai mā o koutou i te whai hoki i tāna whakaaro. He rerekē tō tātou. Āe.
	Ākonga 2:	I kaute au i ngā mea o runga me ngā mea o raro. Nā reira, i kaute au āhua rua o ngā taha.

This interaction came from this teacher’s fourth lesson. In it, a student first provided a description of what he did to determine how many dots were on the sides of a set of dice. The teacher then rephrased the student’s response so that it became a generalisation. Generalisations are important in mathematics (Meaney, 2005), and so it is not surprising to find that the teacher used this as an opportunity to emphasise the value of a more general explanation. This exchange shows that students as well as the teacher affect the scaffolding and modelling which is offered.

The second student provided a response which followed this more general pattern and gave no amounts at all. This suggests that the student was working at the intake stage of the model. He was trying out using a more general description but over-generalised, as he did not provide enough information for someone else to follow what he had done.

Writing the new term in an equation which is related to what has just been discussed
Often, learning to write was introduced after students had gained oral fluency in the use of terms. This is most likely because the symbols for writing mathematics must be learnt separately from conversational te reo Māori.

	T6:	He aha te nama tekau mā waru i ngā wā katoa? Ka tīmata koe i te ( ).
	Ākonga:	Te nama nui ake.
	T6:	Anā, whakawehea.
	Ākonga:	Toru.
	Ākonga:	Ono.
	Ākonga:	Iti iho i te …
	T6:	Ono ka …
	Ākonga:	Toru.
	T6:	Toru. Kei a wai he whakaaro ināianei?
	Ākonga:	Tekau mā waru whakawehe toru.
	T6:	E toru, ka ono.

In this extract, the students had just solved the problem using blocks. The teacher then modelled writing the equation down after she elicited the parts of the number sentence from the students. In particular, she was emphasising the division sign as she wrote it; this was something new for these students.

Giving definitions verbally and through diagrams
It has been suggested that providing definitions of new words supports students’ remembering of these words more than if they just heard them in contexts. Brett, Rothlein, and Hurley (1996) found that students learnt and remembered six weeks later more new words after being given short explanations while stories were being read, than students who heard the same stories, but were not given the definitions. Definitions are essential in mathematics where precise meanings of terms are needed in order for the logic of ideas to be developed. Quite often, these definitions contain a visual representation as this provides information more accurately than a verbal description:

T7:

Kāore he raru mō tēnei. Engari, mehemea kei te kōrero i tērā kei te hoatu i tētahi ingoa ki tērā mea, arā ko te rua tōraro tahi, koinā te taunga. Ki hea tau ai ki runga i te tukutuku? Me ako koutou i ēnei kupu, pūwāhi. Kei te kōrero mō taua wāhi ko te taunga kei te kī koutou, “Kei hea tērā i runga i te tukutuku”.

In T7’s lesson, he defined taunga (co-ordinate) with examples, including visual representations, and then gave students a statement that they could repeat.

Emphasising the relationship between ideas using diagrams or physical materials and words

Especially in junior classes, much mathematics learning revolves around using materials. This learning is often discussed and then recorded on paper. There is, therefore, a need for students to be aware of the terms and expressions that accurately describe the mathematical idea being displayed. The following extract revolves around a child’s representation of 18 pieces of food shared between six people. This child produced three groups of six, rather than the six groups of three that the teacher had expected.

	T6:	Tekau mā waru nērā? E hia kei mua i a koe? Me kaute, tahi, rua, toru, whā, rima, ono, whitu, waru, iwa, tekau, mā tahi, mā rua, mā toru, mā whā, mā rima, mā ono, anā kāti ēnā. Anā, e hia ngā kai mo ia tāngata? E hia, hei aha te tirotiro haere?
	Ākonga:	Pīrangi tētahi.
	T6:	Kua tuhia e koutou te mahi whakawehe i raro iho.
	Ākonga:	Kāo.
	T6:	Tangohia te aha wehe aha kei mua i a koe o whakautu.
	Ākonga:	Ono.
	Ākonga:	Āe.
	T6:	Aua. Mahia tahi, rua, toru, whā, rima tokorima noa ngā tāngata, tokoono nērā. Nō reira, i te hiahia e koe kia hoatu ngā kai ki ia tangata, kua mahia e koe tēnā.
	Ākonga:	Kāo.
	T6:	Kāo. Nō reira, nā, kua pau te katoa o ngā kai. Kua hoatu e koe te kai ki ia tangata, ka pai, ka pai mēnā kua mahia [students chatter] ka pai. Pēhea koe e mōhio ai? Kei te tika koe?
	Ākonga:	Kaute.
	T6:	Āe. I kaute, koe. Whakarongo. He ōrite ngā kai mo ia tangata?
	Ākonga:	Whakawehe … pou rua (?).
	Ākonga:	Tahi, e toru, tahi.
	T6:	Ka pai.

When the teacher saw how the student had arranged her groups, she then drew attention to the fact that six people should be shown by having six groups. After the student rearranged the blocks into six groups, she asked the student what she should do next (Pēhea koe e mōhio ai? Kei te tika koe?). The student responded “count”. The teacher then emphasised that each group should have the same amount in it by asking whether each person had the same amount of food. At this point, another more confident student took over the interaction. This exchange emphasised the relationship between the parts of the problem, including how it was phrased, and the representation. In later lessons where the problem was recorded in symbols, the relationship was emphasised again.

Modelling a new term, skill, or idea as it is being explained
All of the teachers at some time or other did this with a new concept. In the following extract, the teacher was working on the problem 12 + = 30. As this dialogue was going on, both the students first and then the teacher were using an abacus to show how they worked out the answer.

	T5:	Engari, ko tōku hiahia e toru tekau ngā rare kei roto i tōku pūkoro? Āe, koinā tōku hiahia. Nā tekau mā rua tāpiri aha ka toru tekau ki reira kōtiro?
	Ākonga:	Rua tekau?
	Ākonga:	Whā tekau?
	T5:	Kāo, atā titiro. Tekau mā rua ki tōku pukoro nē?
	Ākonga:	Āe.
	T5:	Ānei kē taihoa Ānei kē tōku, ka pai. Anā tekau mā tahi, rua, toru, whā, rima, ono, whitu. Tekau mā rua tāpiri tekau mā …
	Ākonga:	Tekau mā waru.
	T5:	Āe, ka …
	Ākonga:	Toru tekau.
	T5:	Ka pai.

Initially, one student began by putting 12 beads to one side of the abacus and then counting individual beads until they reached 30. To emphasise the concept of “ten” in solving these problems, thus adding meaning to the students’ label, the teacher showed how 12 was part of 30. After first pushing 12 to one side, he then pointed out that there was a whole row of 10 beads in the unknown part, before counting the 8 remaining beads individually. In this exchange, in order for the students to gain an effective method for doing the mathematics, they needed to learn an expanded meaning of the term “ten”.

After teacher explanation, having students say back the new term
When a teacher wanted to reinforce a definition or explanation, they would often finish it by asking a closed question that had a high likelihood of being answered correctly:

	T6:	Kei te piki tonu te mātauranga mo te mahi whakawehe. Nō reira, ānei te tauira. Nā, kei te whoatu ia rākau rānei ki a koutou mā koutou ki te whakaaro. Kia tārai kia mahi te mahi whakawehe. Tangohia ēnei i te tuatahi. Taihoa koutou, kia awhina i a koe. Tuhia hoki te mahi whakawehe nē? Anā, āta whakarongo mm: [folds arms]: he aha tētahi mea? Kāore anō kia whoatu tētahi pātai ki a koe. Nā, tekau ma waru ngā (pirihana) kei te pourewa teitei. I te hiahia e rātou ētahi o ngā kai e iwa ngā kai oh e ono ngā kai anake. E hia ngā kai mo ia pirihana? Anō tekau mā waru, me tini nērā? Tekau mā waru ngā kai rerekē. E ono, ngā pirihana. E hia ngā kai mō ia pirihana? Me mahi?
	Ākonga:	Tango.

In this extract about 18 ÷ 6, the teacher emphasised the relationship between whakawehe (division) and repeated subtraction. The explanation ended with the teacher asking a student how they would work out each person’s share of food. The student responded with “subtraction”.

Having students repeat the final answer after the teacher has modelled finding the solution
Especially in the situation where students were doing a mathematical activity that increased their understanding of the relationship between amounts, a teacher explanation would often result in the solution or answer being repeated.

	T5:	Ka pai, tekau ma ono. Engari, tōku hiahia, ko te rima tekau. Tekau mā ono tāpiri aha ka rima tekau?
	Ākonga:	I wareware au.
	T5:	Kia tere tekau, i rera tekau. I reira, ko tēnei mea, ko te tekau tahi rua ka pērā anā, Ākonga 1. Āta whakarongo kōtiro. Titiro Ākonga 1, taihoa. Āe, titiro mai tekau mā ono tāpiri aha ka rima tekau? Ānei, haramai. Āe tekau mā ono i reira engari ko toku hiahia, ko tēnei mea rima tekau. Anā, titiro tahi, rua, toru tekau, tahi, rua, toru, whā, toru tekau mā whā ka?
	Ākonga:	Toru tekau mā whā.

Previously, T5 had worked on a number of similar problems with the students using abacuses. When a student was unable to work out the answer, the teacher modelled it and gave a verbal explanation. He then had the student repeat the answer.

Relating new terms to already known ones
Very often, teachers would try to make connections between what the students knew already and new material that needed to be learnt.

	T1:	Tēnā pea, he aha anō te kupu kia pēnei kē? Tētahi tangata, kei te …, kei te …?
	Ākonga:	Poutū?
	T1:	Āe, rite ki te pou. Nāreira, kei te tū pou, poutū rānei.

In this extract, the teacher asked students for the word for horizontal (a horizontal line is drawn on the board). Although one student, at least, offered poutū, she did so hesitantly. There are a number of reasons why students may hedge their responses (Meaney, 2006b), but in this instance, the teacher responded by explicitly making the connection between pou (a pole) and the word for horizontal to help students remember poutū.

Using a set of leading questions so that students are channelled into using a particular term
At the beginning stages of a topic when there are new concepts and new aspects of the mathematics register to be learnt, teachers often used a set of leading questions that have limited responses and, thus, are difficult for students to get wrong. This forced students to use new terms or explain them when they perhaps would not have been able to give a coherent description otherwise.

	T6:	Nō reira, nā, māku e hoatu ētahi anō. Nā, e hia i te tuatahi?
	Ākonga:	Rua, whā.
	WT:	E whā, āe, tangohia e whā. Tokohia ngā tāngata?
	Ākonga:	Tokorua.
	T6:	Tokorua. E hia ngā rare e …?
	Ākonga:	E rua.
	T6:	E rua, ka pai.

In this extract, the teacher was introducing division. She had the students read a division problem and model it with the blocks. However, in order to ensure that the students understood each part of the problem, she asked about their relationship to what they had modelled. A wrong answer by one student (rua) prompted her to ask very restricted questions that students could not get wrong. Wood (1998) suggested that this type of “funnel pattern” was of limited value to students in learning mathematics. This is because the teacher is the one who is doing the cognitive work. However, if these leading questions are only used in introductory tasks, they can force students to use, both through interpretation and production, aspects of the mathematics register that they would not normally use. This then helps to ensure that new language is repeated regularly and, thus, has greater likelihood of being acquired.

Using fill-in-the-blank sentences
As can be seen in the previous section, using unfinished sentences can also be a common strategy for channelling students into using particular terms.

	T1:	He aha tāu i kī mai?
	Ākonga:	Rua tekau mā whā.
	T1:	Rua tekau ma …?
	Ākonga:	Whā!

Here T1 had a student, who had supplied an appropriate answer, repeat it for those students who were struggling to follow the discussion. She did this by starting the sentence and leaving the student to complete it.

Acknowledging the difficulty of learning some terms or ideas
Students can become aware that learning new terms and expressions is a large part of a particular lesson. The teacher can also support students’ awareness of the importance of this aspect of a lesson by acknowledging the difficulty of it in regard to mathematics learning.

	Ākonga:	Āe, tērā mea i konei kei runga.
	T7:	Nā, ko te kotinga “t” he tōrunga, he tōraro rānei?
	Ākonga:	He tōrunga.
	T7:	Tōrunga. Engari kāore tātou i te mōhio, nō reira, tāpiri.
	Ākonga:	Tāpiritia te “r”, oh, he “k”.
	Ākonga:	He aha?
	T7:	Āe, tāpiritia te “k” i tēnei wā.
	Ākonga:	“W”, oh, rima e ( ).
	T7:	Arohamai, i hoatu i tētahi mea uaua ki a koutou. Kei te tere whakaatu pēhea te kimi i te “k”.
	Ākonga:	Ka taea te whaka, ah, ( ) atu i ngā rārangi mō te mahi tukutuku. I te mea he tino uaua, āe, ki ngā mātua.
	Ākonga:	Āe. Nā, te mea kāore e taea te kite.

In this extract, there was a discussion of the r (x) and t (y) co-ordinates and the t-intercept (k) in regard to the equation for a straight line, t = pr + k, (y=mx + b). This discussion began with ideas about the terms for a particular line. When the students showed confusion over the meaning of the different terms, the teacher acknowledged that it was difficult to learn all the words. One student followed this up by saying that it would be very difficult to explain it to parents and this was confirmed by another student.

Providing a rationale for the need to learn a new term or idea
Teachers only provided a rationale for what was being learnt to older students. The rationales gave a context for what was being learnt that connected it to future learning or outside school experiences.

	T7:	Ko ēnei wāhi katoa i runga i tēnei rārangi. Kei te tika mō tēnei, engari kotahi te wāhi. Kei te ōrite mō ngā mea e rua, nā, koinā te mea. Kei te tino hiahia tātou i tēnei rangi ngā wāhi e tutaki ai ngā rārangi i te mea. Ka taea e tātou te mahi hei aha te tukutuku? Nō reira, kei te ako koutou i ētahi nuka nē? I te mea i roto i te tātai. He pai, ki te tuhi tukutuku, engari ko ngā tohunga tata. Kei te hiahia kia waiho ki te taha hiahia ana kia mahi noa iho i ngā whāritenga, engari koinā tā koutou mahi i tēnei rā me apōpō. Nō reira, :[puts new sheet on projector]: tukutuku hou. [boy stands up to move to other side of class]: Āe, Ākonga 1 kia tūpato te tirotiro ana ka tuhi i ngā rārangi e rua anō. Ā Ākonga 2 hei aha okei rua ngā rārangi “a” “e” rārangi “a”.
	Ākonga:	Kāore e taea te kite.

The teacher provided a rationale for understanding the relationship between graphs and their equations by stating that equations give points and, thus, are shortcuts for describing lines.

Requesting students’ attention before introducing a new term
In most of the lessons, there were requests for the students to pay attention to what the teacher had to say. These requests were common when new terms were about to be introduced and the teachers wanted students not to miss what was said or done.

	T7:	I runga i te tukutuku ko tētahi. Kei konei ko tērā atu, kei konei kotahi, anahe te wā kei te ōrite. Nō reira e ai ki tēnei ko- nā he mea nui tēnei. Waiho wā koutou pene rākau ki raro ruri ki raro titiro katoa mai ki mua nei: [boy coughs].
	T7:	Ki konei tēnei wāhi ka tutaki he aha te “t”?

In this lesson, the teacher wanted students to pay attention to where the point of intersection was of two lines and how this related back to the equations of the lines. Requests for attention were also part of the integration stage. At the noticing stage, students need to pay attention because new material is being introduced whereas at the integration stage, students are being encouraged to make use of the skills and knowledge that they already have.

Describing a new term as being important in a subsequent lesson
It was only in the older class that links were made to what students could expect to learn in subsequent lessons.

	Ākonga 1:	Te tahi.
	T7:	Tēnei taunga, tēnei pūwāhi, he aha te “t”? Ki konei toru. Ka taea tētahi atu “t” i tērā wāhi?
	Ākonga 1:	Kāo.
	T7:	Kotahi te wāhi te “t” e rite ana ki te toru. Nē, nō reira. i tēnei wāhi, ko te “t” kei konei me te “t” kei konei e rite ana ki te toru nē? Kāore tātou i te kōrero mo te “t” e rite ana ki te whā. Te “t” e rite ana ki te rua te, aroha, te “t” e rite ana ki te whā tō raro. Kei te kōrero mo te “t” e rite ana ki te toru. Nō reira, i runga i tērā kei te kī mehemea ko tēnei e rite ana ki te toru. He aha tēnei e rite ana ki te toru he aha te whanaungatanga o tēnei ki tēnei?
	Ākonga:	Ka toru ngā mea e rua.
	T7:	Ka toru ngā mea e rua. Nē, nō reira he aha te whanaungatanga o te mea o runga ki te mea o raro nui atu rānei iti iho rānei rite rānei?
	Ākonga:	Rite.

This extract followed on from the extract quoted immediately above it. In it, T7 emphasised the whanaungatanga (strong relationship) between the two lines. The teacher made it clear that this was something that would be important in subsequent lessons.

Intake

At this stage, students are expected to use the language either through listening, speaking, reading, or writing, but not fluently. By experimenting with how the new terms and expressions are used, the students can consolidate their meanings and their understanding of where and how they are used. Previous research had shown that students develop a very limited definition of new terms if they do not hear the terms or use them themselves in multiple situations (Noridah & Clements, 1999; Skemp, 1971; Whitland & Pegg, 1999). Unless students have a shared understanding of the meaning of different terms or control of important grammatical structures, they will not be able to use these aspects of the mathematics register effectively in their mathematical discussions or activities. At this stage, most of the learning revolves around “doing mathematics”. What is emphasised is not the language, but the solving of problems, of which being able to use the new meanings or terms or expressions is an implicit part.

Having choral responses with the students
At the early stages of having students use new mathematical terms, teachers in the junior classes often recited counting patterns with the students.

	T3:	Whitu mai te whitu toru, whā.
	Katoa:	[Clap hands counting] Whitu, waru, iwa, tekau, tekau mā tahi, tekau mā rua.
	Ākonga:	Tekau mā whitu.
	T3:	Oh, kāti. Kua rongo au ki tētahi hē. Me tīmata anō mai te toru. Kua reri toru, whā.
	Katoa:	Toru, whā, rima, ono, whitu, waru, iwa, tekau, tekau mā tahi, tekau mā rua, tekau mā toru, tekau mā whā, tekau mā rima, tekau mā ono, tekau mā whitu, tekau mā waru, tekau mā iwa, rua tekau.

The teacher had the students “count on” from whitu (seven) and joins the students in reciting the numbers and clapping hands. However, when one student miscounts, she stops the counting and then has them count from toru (three). She again joins in with them.

Having students as a group do choral responses
If students are able to do a choral response without any support from the teacher, it is likely that they worked at the output stage of the Mathematics Register Acquisition model. However, in some circumstances the teacher may support the students’ group choral responses in other ways than just jointly reciting numbers with the students. Without this extra support, it was unlikely that at the intake stage, the students could have done the task on their own.

	T2:	Tuatahi, mā tātau katoa e whakamahi tērā mahi. Tere whakamahi hoki i ō koutou ringa [uses his fingers to model the counting].
	Ngā ākonga:	Tahi, rua, toru, whā, rima, ono, whitu, waru, iwa, tekau, tekau mā tahi, tekau mā rua, tekau mā toru, tekau mā whā, tekau mā rima, tekau mā ono, tekau mā whitu, tekau mā waru, tekau mā iwa, rua tekau.
	T2:	Nā, ka mahi tere ka mahi tātau mai i te tekau ki te tahi, nē? Kua reri [uses fingers to show counting].
	Ngā ākonga:	Tekau, iwa, waru, whitu, ono, rima, whā, toru, rua, tahi, kore.

T2 supported his Year 0 students’ counting by showing his fingers increasing and decreasing in time with the recitation of the numbers. Some of the students mirrored using their fingers to support their counting.

Giving the first syllable of a term so that students are reminded of the term and then complete it
At the intake stage, the teacher channeled students into using the new aspects of the mathematics register so that they have no choice but to use it. Consequently, students were often heavily prompted:

	T6:	He aha te ingoa o ēnei mea?
	Ākonga 1:	Ko te tahi me te hāwhe.
	T6:	Kāo, he aha te ingoa o ēnei mea?
	Ākonga 2:	Ngā whakawehe!
	T6:	Āe he aha te whakawehe?
	Ākonga 2:	Ngā haurua.
	T6:	Ngā hau …?
	Ākonga 3:	Whā?
	T6:	Kāo, ngā hautau, nē? Me maumahara koutou, nērā?
	Ākonga:	Āe.

In this example, the teacher started the lesson by asking about what the students had been learning. A student’s inappropriate response (one and a half) resulted in the teacher asking the question again. Another student suggested division and the teacher asked for more details. The student gave a response that included a mispronunciation. Rather than correct it, the teacher repeated the correct part with a rising intonation, suggesting that the student should complete the term with another syllable. A different student provided another wrong syllable. The teacher then returned to the noticing stage by giving the complete word for fractions, hautau, and asking students if they remembered it.

Asking students for names, definitions, or explanations of terms
With the older students, the teachers can check on their understanding by asking them for definitions. If the definitions are concise and clear, then the students are at the output stage. When the teacher or other students has to provide extra clarification, prompts, or information, then the students are more likely to still be learning how to use the terms and so would be at the intake stage:

	T7:	Inanahi, i tuhi au ngā rārangi e rua me te pātai ki a koutou. Ah, kāre, i te pātai he tono ki a koutou, kōrerohia mai te tutakitanga o ngā rārangi e rua. Nō reira, Ākonga 1 haere ki te tuhi i ngā rārangi e rua.
	Ākonga 1:	E ai ki tōku mea.
	T7:	Oh, koinā tāu e kī ai he rerekē.
	Ākonga:	Whā ripeka, oh, māku e tuhi engari, pātai māu e whāki mai.
	Ākonga 1:	[Stands up and goes towards whiteboard.]
	T7:	Ākonga 2, hoki ki a koutou kei te pai kē mehemea i tino pango te rārangi o waenganui o ngā tua, he uaua te kite i runga i tēnā.
	Ākonga 2:	Oh.
	Ākonga 1:	Oh he aha tēnā?
	Ākonga 2:	Oh.
	Ākonga:	Whā kei runga rua ki te taha.
	Ākonga:	I whakaaro au i tuhi au e rima.
	T7:	Koinā te tutakitanga, nē?

In the extract, the teacher commanded a student to explain what was happening when two lines met on the graph (tutakitanga and rerekē). The student went up to the whiteboard and was helped in the explanation by suggestions from other students and from the teacher.

Having the students model use of terms, skills, or ideas
This is very similar to the first strategy described in the noticing section, that of providing opportunities for the new term to be used appropriately. At the intake stage, the teacher is ensuring that the students are the ones who are using the new terms, although often in limited ways. In the next example, the teacher had set up an activity in which the students had to describe the arrangement of some coloured multi-link blocks. The teacher, therefore, had instigated the use of the language but the students were the ones who were actually using it.

Ākonga:

I kī au, e rua ngā whero e kopae ana ki raro, e toru oh e rua ngā um e toru ngā oh e rua ngā kākāriki e ruapae ki runga me tētahi kōwhai ki raro. I te, um, i te, um, kākāriki kore tētahi papa ki raro.

In this utterance from T1’s fifth lesson, the student was describing how different coloured multilink blocks had been placed together. The student used ruapae instead of huapae to talk about how the blocks were lying horizontally. This student was still learning how to pronounce this word, but was also trying out when it should be used. Huapae was a term used earlier in the lesson by another student and it could well be that the student recognised it and realised that it was needed in his own description, but was still learning how to use it appropriately.

Asking students for examples of a term
As well as seeing students asked for definitions, the intake stage sees students being asked for examples of terms. This is different from the noticing stage, where the teacher would be the one providing the examples.

	T7:	Nō reira, i runga i tērā he aha te rōnaki o te rārangi e tuhia nei e ia ināianei? mehemea e toru kei runga tētahi ki te taha katau.
	Ākonga:	Toru, tahi.
	T7:	Whakaarohia i mua i te kōrero noa. He aha te rōnaki?
	Ākonga 1:	Toru tahitanga.
	T7:	He tangata kei te mōhio?
	[Boy puts up hand]
	T7:	Āe, he aha?
	Ākonga 2:	Toru tahitanga.
	T7:	Haere tonu.
	Ākonga:	Rua.
	T7:	Āe koinā te whāritenga engari, ka kī tātou ko te toru tahitanga.
	Ākonga:	Kāre he tikanga mo te tahitanga.
	T7:	Ka kōrero, āe, toru rau toru tahitanga hei āwhina i a koe ki te tuhi, ka pai kei a koe te ruri?
	Ākonga:	Āe, kei kōnei, āe.
	Ākonga:	Patua woah.
	T7:	[Gives Ākonga 1 ruler] Te tutakitanga koinā tā koutou mahi kāinga.

In this example, the teacher introduced the term rōnaki (gradient) into a discussion on straight lines. He then asked for an example from the graph of two lines that was on the board. A suggestion was made, but the teacher rejected this by reminding students to think before they speak, whakaarohia i mua i te kōrero. Another student rephrased the original suggestion, but the teacher rejected it by saying he tangata kei te mōhio (doesn’t anybody know?). These reminders to think are common at the integration stage. However, as they did not elicit the appropriate response, the teacher was forced to provide the supporting details needed to make the students’ suggestions adequate.

Using the similarities between concepts as an entry into having students reflect on the differences
Often in mathematics classrooms, language learning consists of adding another layer of meaning to terms that students are already familiar with. In some cases, students may already be making use of the new meaning, but in order for it to be used in the next phase of their learning they need to discuss it explicitly. The teacher’s role, therefore, is to channel them into describing what they already know, but had not previously verbalised.

	T5:	He aha te rerekētanga Ākonga 1 o tēnei?
	Ākonga 1:	Ngā rerekētanga ko te tekau.
	T5:	Nā, he aha te rerekētanga Ākonga 1 o tēnei mea? Mēna e tuhia mai ēnei kei runga i te …?
	Ākonga 2:	He kore.
	T5:	Āe, he aha te tikanga o te kore?
	Ākonga:	Tau tekau.
	T5:	Āe, he tohu tekau pea.
	Ākonga:	Tahi.
	Ākonga:	He nama kore.

The teacher wanted to make explicit to the students the relationship between the digits so that they would be able to describe the relationship between 5 + 3 = 8 and 50 + 30 = 80 in terms of tens. He tried to do this by drawing the students’ attention to the zeros in the ones column and asking what they stood for. The students struggled to give a coherent response.

Having students draw their own diagrams or use materials to show a particular term
As well as teachers using materials to help support students, they often encouraged students to visually present their understandings about an idea that they are learning.

	T7:	Te pūwāhi o te tutakitanga he aha tērā Ākonga 2?
	Ākonga 2:	Um.
	T7:	Te tū- te pū- wā- ah taunga o te putahitanga, i hea koe i te moe tama?
	Ākonga 3:	Whā, rua, toru, rima.
	T7:	Kī mai whā rua, whā, oh, taihoa kei te tika tērā?
	Ākonga:	Whā rua.
	T7:	Whā rua?
	Ākonga:	Rua whā.
	T7:	Rua whā. Nō reira kei te kite koutou kei te miki rapu ētahi wāhanga o te mahi nei, tērā atu rārangi kia tere e tama.
	Ākonga 4:	I hea i hea tērā.
	Ākonga:	( ) tuawhā.
	Ākonga:	Koirā te taunga.
	Ākonga:	Rima, rima.
	T7:	Tāu e kōrero ana ko te rōnaki ko te pūwāhi, kei hea tērā i runga i te “r” e rite ana ki te rua te “t” e rite ana ki te whā? Āna ka tuhi i ngā taunga kia pēnei nō reira, he aha i runga i te “r” e ai ki tēnei rua?
	Ākonga:	Kāo.
	Ākonga:	Rima rua.
	T7:	Rua.
	Ākonga:	Me …
	T7:	Whā. Ka pai, āe, kia tere tērā atu rārangi e tama.
	Ākonga 1:	He aha tērā atu?
	Ākonga:	He aha?
	Ākonga 1:	He aha te rārangi e haere pēnā ai?
	T7:	Rua toru tōraro. Te tutakitanga [pulls chair out to sit down], kei te tohu te tutakitanga i te aha? [Sits down on chair.]

In T7’s class, Ākonga 1 drew points and then lines on the board during the discussion about rōnaki (gradient) to illustrate it. The teacher encouraged other students to make suggestions, but provided support and clarification when the suggestions were not clear or appropriate. The students then made their own drawing to illustrate the idea of rōnaki. This clarification by the teacher provided a model of an appropriate answer for the students, but used their contributions as a basis for this (Bill et al., 1992).

Repeating or having students repeat appropriate responses
If a teacher believes that the students are still consolidating their understanding of new ideas or language, they will often reinforce when they have used the ideas correctly by repeating the answer. Bill et al. (1992) found that in a 10-minute extract of a classroom discussion over half of the students’ responses were repeated by the teacher. In our videotaped lessons, the proportion of students’ responses that were repeated was not as high. Rather the teachers at this kura used a range of different strategies when they believed that the students were working at the intake stage.

	T5:	Tāpirihia te waru tekau ki te toru tekau?
	Ākonga:	Tahi rau tahi tekau.
	T5:	Tahi rau tahi tekau, ka pai. Tāpirihia te iwa tekau ki te whā tekau?
	Ākonga:	Tahi rau toru tekau.
	T5:	Tahi rau toru tekau, kei te tika ia?
	Ngā ākonga:	Āe.

When T5 introduced adding tens, he asked a series of questions of the students to ensure that they understood the relationship to single digit addition calculations. Several times, he repeated students’ correct answers. At the end of the interaction, he asked the students if they agreed with the answers that had been offered.

Elaborating on students’ responses in words and with diagrams
At all class levels, teachers who felt that students were still at an early stage in learning a concept would take an incomplete response of a student and expand it to illustrate the point that they wanted to get across.

	T6:	Timata koe he aha te mahi whakawehe?
	Ākonga:	( )
	T6:	Ka pai, anā he aha te whakautu?
	Ākonga:	Tokowhā.
	T6:	Nē.
	Ākonga:	Oh, rima tekau.
	T6:	Rima tekau. Tokohia ngā tāngata? E hia ngā rare mā ia tangata? Rima tekau?
	Ākonga:	Rima.
	T6:	Pēhea koe e mōhio ai tekau o ngā rare mo ia tangata?
	Ākonga:	( )
	T6:	Āe. Pehea koutou e mōhio ai tekau o ngā rare mo ia tangata? Ākonga 1, he aha ō whakaaro?
	Ākonga 1:	( )
	T6:	Ko te nama tuatahi ko te aha kia mōhio ai koe? Ko te nama tuatahi mōhio ai koutou. E hia ngā aha …?
	Ākonga:	Ngā tāngata.
	T6:	Ngā tāngata. Ka pai, te nama tuarua kia mōhio ai koutou e hia ngā …?
	Ākonga:	Rare.

Although the quality of the videotape recording meant that many of the students’ comments were not audible, all of their answers were quite short. The teacher, however, took each one and expanded it into a word problem. This highlighted for the students the different parts of a word problem, and knowledge of these parts was reinforced later in the lesson when the students began to write the problems as number sentences.

Asking further questions to help students reflect on what they were describing
The teacher would do this to check on what the students knew or had done. This strategy included checking that students had understood the different parts of a problem or idea.

	T1:	Tapirihia te maha o ngā mata ki te maha o ngā akitu, kua puta kē ko tetekau, ne ha? Te maha o ngā tapa me kī waru ināianei, he aha te huarahi e whai ake? Ae!
	Ngā ākonga:	Ko te tekau?
	T1:	I te mea anei kē te nama hou, mo te maha o ngā tapa, ka tapirihia kia rua, kua …?
	Ngā ākonga:	Tekau!

The teacher began with a general request for students to describe their strategy for working out the answer. The students’ hesitant response suggested that they were unsure that 10 was the answer. The teacher then rephrased her question so that the students were channelled into providing tekau. Thus, they were reassured that in this situation tekau had the appropriate meaning. The teacher was very much in control of how the interaction developed.

Having students provide a rationale for what they are learning
In the noticing stage, the teacher of the older students had given them a rationale for why they were learning about the intersection of straight lines. T6 also asked her students for a reason for what they were learning. This suggests that having a rationale for what they were learning can be appropriate for students of different ages.

	T6:	Nō reira, he aha te tikanga o te mahi whakawehe?
	Ākonga:	Kia mōhio e hia ngā rare?
	T6:	Āe, kia mōhio e hia ngā rare, ngā kai aha rānei mo ia tangata kararehepereti aha rānei, nērā?

The teacher asked the students what they could do with whakawehe (division). One student stated that it could be used for grouping lollies. The teacher elaborated this by stating that it could be used for dividing lollies or food among people.

Ignoring inappropriate answers and just acknowledging appropriate ones
In investigations of mathematics classrooms, there has been much discussion about the acceptance of inappropriate responses by students (Williams & Baxter, 1996). In regard to the learning of new aspects of the mathematics register, this strategy would seem to be associated with the intake stage.

	T5:	Tērā kōrua, tāpirihia te rima tekau mā toru ki te whā tekau mā ono?
	Ākonga 1:	Tahi rau toru.
	Ākonga:	Tāpiri aha?
	T5:	Whā tekau mā ono.
	Ākonga 1:	Iwa tekau mā iwa.

In this example, two students were asked to work out the problem using an abacus. One student’s wrong answer was ignored, most probably because the other student who had been using the abacus asked a clarifying question. This meant that the teacher had an option to respond to the second student in the hope that he would determine the correct answer. The teacher also modelled how to work out the answer using the abacus. Consequently, the original student was able to provide the correct answer.

Querying students’ inappropriate responses
Almost all the teachers used this strategy at one time or other and several examples have already been provided in the examples for other strategies. Quite often, rising intonation was used to suggest to the student that their answer was wrong. Teachers would also query students if their responses were unclear or needed elaborating.

	T1:	Nā reira, he ira kei ia taha nē? Kua piri pēnei, e hia ngā ira kāre e ahei te kite ākonga 1?
	Ākonga 1:	E whā?
	T1:	E whā! Nā reira, he aha te huarahi e whai ake i tēna kia tae atu ki te …?
	Ākonga 1:	Tango.
	T1:	Āe?
	Ākonga 1:	Tango whā mai te tekau mā waru?
	T1:	Ka …?
	Ākonga 1:	Ka tekau mā whā!
	T1:	Tekau mā whā!

T1’s queries of Ākonga 1’s statements forced the student to provide more details so that a more complete response was given.

Suggesting that students’ inappropriate responses are close
There are a number of ways that a teacher prompts students to use new aspects of the mathematics register. When they were doing a mathematical activity, there was often a need to use the added layers of meanings of already familiar terms.

	T5:	Tāpirihia te whā tekau mā iwa, āta titiro kōrua he tika tēnā kei te hē nē, tāpirihia te toru tekau mā whitu
	Ākonga 1:	He aha te whakautu?
	T5:	He aha te whakautu?
	Ākonga 1:	Waru tekau mā whitu
	Ākonga 2:	Kāo.
	T5:	Kāo.
	Ākonga:	Tata.
	T5:	Tata.
	Ākonga 2:	Kāo i kī koutou tērā.
	T5:	Kāo, āta titiro, tama. Kua tāpirihia tēnā nē tahi rua toru, toru tekau mā whitu, ki tēnēi mea whā tekau mā iwa, nē?
	Ākonga 1:	Whā tāpiri toru tahi rua toru. Oh, whitu tekau mā whitu.
	T5:	Whitu tekau mā whitu. Kāo, he mea uaua tēnā. Āta whakaarohia, tīmata mai i tō ake mea whā tekau, āta titiro whā tekau mā ono.
	Ākonga 1:	Waru tekau mā ono.
	Ākonga 2:	Ka pai.

In this extract, T5 gave the students 49 + 37 to work out on an abacus. In one pair, one student worked out the answer to be 87. The other student and then the teacher said “no”. The student and the teacher then said that his answer was close (tata). The teacher talked through solving the problem by moving the beads on the abacus across. The student then suggested that the answer was 77. The teacher stated that the answer was wrong. The student then gave the answer 86 and his partner affirmed this with ka pai.

Having students work backwards from an inappropriate answer to the question which was asked
In prompting students to use new aspects of the mathematics register, T1 used students’ wrong answers to focus them back onto the original question. The extract is from a lesson in which students arranged face-to-face 5 blocks that had dots on each face. The class had discussed the minimum number of dots that could be seen and a suggestion was made that this number was 22.

	T1:	Ānei tētahi whare! E hia ngā ira kei te kite atu inā kua huri haere? Rua, whā, ono, waru. Kua rite?
	Ākonga:	Āe.
	T1:	Kua rite? Tekau mā rua. Ko te mea rahi rawa i tēnei wā! Karekau he mea kē atu?
	Ākonga:	Tekau mā iwa, tērā.
	T1:	Tekau mā iwa. E hia tamariki mā! Rua kāore i te kite, e rua anō kāore i te kite, e rua kāre i te kite i kōnei nēhā? E hia katoa?
	Ākonga:	Waru.
	T1:	E waru! Ka tangohia te rua tekau i te … e hia katoa?
	Ākonga:	Rua tekau mā rua
	T1:	E hia ngā ira katoa?
	Ākonga:	Rua tekau mā rua.
	T1:	Kāo, aroha mai, inā wehe atu i ngā mataono?
	Ākonga:	Toru tekau.
	T1:	Toru tekau. Nā reira, aroha mai. Ka whakaatu kia rua tekau mā whā rānei! Āe?
	Ākonga:	Kāo!

The student’s response, that they had a building that only showed 19 dots, resulted in the teacher asking the student to count the missing dots (8) to work out that the total number of dots was 22.

T1 then reminded the students that the original problem was about whether they could arrange the blocks together so that they would show fewer than 22 dots (Ko te pātai tonu; Ka ahei au te hanga i tētahi whare e nui ake i te rua tekau ma rua ira?). The teacher then asked whether the students thought that the student’s building fulfilled this criteria and they responded “Kāo” (no).

Using specific amounts to illustrate a general rule or idea
Sometimes when students are introduced to a general rule that can be applied in a number of situations, the teacher models how it is used by relating it to specific numbers. At other times, students’ calculations using specific numbers were used by the teacher to move them into describing a general rule.

	T1:	Kōrua, he aha tāu mahi kia toru tekau?
	Ākonga:	E rima kei runga e rima kei raro ka tekau. Ono kei muri e whā kei mua ka tekau, tāpiri e whā kei muri me ngā taha me ngā taha e whā me kotahi te ( ).
	T1:	Kia ora rawa atu. He pai hoki tō reo ka rongo, he aha tāu ah kia kite atu i pēnei kē nēhā ki tōku kei te rongo koe? [Ākonga 1] tāpirihia ngā ira kei te noho kei runga nei ki ngā mea i raro kāore i te kite nēhā. Ka tekau nē katahi kī mai ka tīmata ki ngā ira kei muri rā anō e ono tērā me wēnei ka tekau, nā reira e ono i kōnei ka taea e koe te kite ināianei tonu [Ākonga 1] me tērā taha. ko wai mā o koutou i te whai hoki i tāna whakaaro he rerekē tō tātou?
	Ākonga 1:	I kaute au i ngā mea o runga me ngā mea o raro. Nā reira, kaute au āhua rua o ngā taha.

In this extract, a student gave a response using specific numbers. However, it was very much context dependent, with the student using their building to illustrate where the numbers came from. The teacher rephrased this response to emphasise the relationship to a more specific equation. This meant that the student’s response became much clearer and less dependent on having the actual blocks.

Focusing students back onto the main idea being discussed to help solve a problem
Students may need to be reminded about the topic of conversation. This can often be a word problem. By having students respond to it, teachers are able to encourage them to use new aspects of the mathematics register.

	T7:	Nā whakaarohia kua huri noa iho, kua hurihia ngā mea e rua whakaaro mehemea kei ahau ono ana kei te tangohia te rua torutanga anahe, he aha kei te toe ki au mahia ki roto nei? [Points to his head].
	Ākonga:	Whā.
	T7:	Kei te karanga noa
	Ākonga::	[Raises hand] Rua.
	T7:	Rua.
	Ākonga:	Āe, i te mea rua torutanga nō reira, toru, rua ā kei te tangohia, ka ono. Ka tini noa e rua.
	T7:	Āe.
	Ākonga:	Ono, whā.
	T7:	Kei te raruraru ētahi o ngā whakaaro whakarongo ki tēnei, he aha te mea nui ko te tahitanga rānei ko te rua torutanga rānei he aha te mea nui ko wai kei te mōhio?
	Ākonga:	Tahi.
	T7:	Ko te tahi, nō reira, he aha te ono tangohia te tahi?
	Ākonga:	Rima.
	T7:	Rima. Engari i kī mai koutou ko te tahi he nui atu i te rua torutanga whakaarohia anō ngā pikitia e tika ana kia kei tēnei taha, e ono kei tēnei taha ko te rua torutanga noa iho kāre anō kia tahi nō reira, ko te otinga ka nui atu i te rima nē.
	Ākonga:	Āe.

In this extract, the class was working on  The students made suggestions about how to work out k. T7 focused the students back on the equation as he talked them through rearranging it. He did this through using leading questions and fill-in-the-blank sentences.

Using student-devised terms in giving an explanation
Forcing students to describe a new concept when they have not yet gained the language can result in them using their own terms. In such instances in this study, the teachers would then use those terms to model a more mathematically-appropriate response.

	T7:	He aha te wāhi e rite ana tētahi whāritenga ki tētahi atu?
	Ākonga:	Te “t” āe.
	T7:	He aha ai?
	Ākonga 1:	( )
	T7:	Koinā tētahi kōrero anō Ākonga 1, he mea nui tērā.
	Ākonga 1:	( )
	T7:	Whakamaramahia anō tō kōrero.
	Ākonga 1:	( ) whā ōrite whāritenga ki te tutakitanga o ngā rārangi, ah, pūwāhi ōrite.
	T7:	Pūwahi ōrite, mehemea ka kōrero mō ngā pūwāhi ahakoa kei kōnei, ahakoa kei kōnei, ahakoa kei kōnei, ngā mea katoa ka tika mō.
		tēnei nē nā i tēnei rārangi kōnei, kōnei, kōnei, kōnei ngā mea katoa ka.
		tika mō tēnei nē kōtiro nē kei runga waiho.

In explaining in her own terms what tutakitanga (point of intersection of two lines) was, the student used pūwāhi ōrite. The teacher repeated this term to remind students about what they already knew about the points on a line and how this related to the point of intersection.

Going over an activity which requires the use of the new language as a whole class before expecting students to do the activity as individuals
After an oral discussion, teachers often supported students’ individual efforts to write their own descriptions or explanations. It was, therefore, important that the students were clear on what was expected of them.

	T4:	Ka haere tētahi whārangi pēnei ki ia tangata ki ia tangata, tā koutou mahi ki te tapahi i ngā kararehe me ngā pikitia rerekē.
	Ākonga:	Me ngā ingoa?
	T4:	Kāo, me whiri katoa tēhea te pouaka ko tēhea te wāhi tika mō ia pikitia mō ia pikitia arā i kitea i te ngahere. Nō reira, ka whakapiri ngā mea i kitea i te ngahere. Kei kōnei pea i kitea tērā pea kāore rawa i kitea i te ngahere i kōnei, nō reira, i kite ia i tētahi kiore.
	Ngā ākonga:	Āe, kāo.
	T4:	Tērā pea i kitea āe tapahi whakapiri ki te pouaka tērā pea. Pēhea ngā ika? I kite ia i tētahi ika i te ngāhere?
	Ngā ākonga:	Kāo.
	T4:	Nē whakapiri ki te wāhi, kāore rawa i kitea i kite ia i tētahi rākau?
	Ngā ākonga:	Āe.
	T4:	Whakapiri ki tēnei taha, kia mutu te whakapiri i āu pikitia katoa ka wātea ki te whakakarakara i ngā pikitia [students cheer].

In this example, after an extensive discussion over two days about what Little Red Riding Hood would see in the forest, the teacher handed out a worksheet with pictures of different animals. On the worksheet were three columns and the students had to decide which column each animal could be pasted into. The columns were i kite, tērā pea, and kāore i kite (can see, perhaps could see, and can’t see). The teacher discussed with the students which columns the different animals could be pasted into before students went and did the activity individually.

Showing students the relationship between what they already know and can do and the new language term or skill
In order for students to learn to use new aspects of the mathematics register when doing mathematics, teachers would channel them into making a connection between what they already know and the new idea.

	T6:	Kei runga i te rākau i te tārai ngā makimaki e whā kia tangohia ngā panana, e hia ngā panana mo ia makimaki?
	Ākonga:	Whā.
	T6:	Tekau mā rima ngā panana kei runga i te rākau, e whā ngā makimaki e tārai ana kia tangohia ngā panana E hia ngā panana mo ia makimaki?
	Ākonga:	He uaua tērā.
	T6:	Tekau mā, oh, ka taea?
	Ākonga:	Kāo.
	T6:	Nō reira, me aha?
	Ākonga:	Āe ka taea.
	T6:	Nē.
	Ākonga:	Kāo, kāo, kāo.
	T6:	Me mahi ka taea, nō reira, me aha?
	Ākonga:	Me tango.
	T6:	Ka taea koe te uru te whā kei roto i te tekau mā rima?
	Ākonga:	Kāo, āe.
	T6:	Āe, engari.
	Ākonga:	Kāore, e taea te hanga e whā o ngā rōpū.
	T6:	Ka pai, kāore koe ka taea te hanga ngā rōpū ōrite nērā, nō reira, tekau mā rima mehemea i a mātou tekau mā rima ko tēnei te whakarau aha?
	Ākonga:	Whitu.
	Ākonga:	Rima.
	T6:	Rima. Na reira e hia ngā makimaki ināianei?
	Ākonga:	Toru.
	Ākonga:	Tekau mā rima.
	Ākonga:	Whā.
	Ākonga:	Toru.
	T6:	I kī mai koe ko tēnei te whakarau rima, ka pai. No reira e hia ngā makimaki ināianei?
	Ākonga:	Whā.
	Ākonga:	Tekau mā rima.
	WT:	Tekau mā rima. E rima ngā makimaki e tārai ana kia tangohia ngā …?
	Ākonga:	Panana.
	T6:	Ngā panana. E hia ngā panana mo ia makimaki?
	Ākonga 1:	Rima.
	Ākonga:	Kāo.
	T6:	E rima ngā makimaki, Tahi, rua, toru, whā, rima. He whakaaro anō koe, ka pai Ākonga 1 kua tino māu i akoe tēnei mea?
	Ākonga:	Āe.
	WT:	Āe, me tuhi koe te nama i whakawehe koe i te tuatahi.
	Ākonga:	E rua.
	T6:	E rua. Ngā aha kaute anō e hia tahi, rua?
	Ākonga:	E toru.
	T6:	E toru, ka pai.

In this long exchange, the teacher used a series of questions to illustrate to the students that they had the skills to work out how to make even groups from 15 blocks. The original problem required the students to work out how many monkeys there were and then how many bananas each monkey would get if 15 bananas were divided evenly. The teacher’s questions reminded the students of the information and the skills (modelling with the blocks) they would need to work out the answer.

Having students answer a series of closed questions to lead them to using the new term, skill, or idea
At the noticing stage, leading questions were used to channel students into saying, reading, or writing a specific term. At this stage, the emphasis was on making students aware of when and how a new aspect of the mathematics register was to be used. In several of the examples above, leading questions were used in this way.

	T2:	Nē anā ka taea e tātou te mahi tērā ināianei me tīmata tātou ki te mahi i ngā pātai o Matua T2, ngā mahi tāpiri whakarongo mai ka hikoi atu a [Ākonga 1] ki te toa ka hoko a [Ākonga 1] e whā ngā rare ka kite ia e toru ngā tiakrete. Ka hoki ia i ērā e hia katoa ngā tiakarete i a [Ākonga 1]?
	Ākonga:	Whitu.
	Ākonga:	Whitu.
	T2:	Ka pai, anā ināinanei kei roto i tērā mahi, kua whakautu kē mai koutou whakaatu mai ngā pātene i ngā tiakarete anā whakaatu mai, e hia ngā rare [students pick up buttons] anā me whakaatu mai, e hia ngā tiakareti nē i kōrero a matua mō ngā rare i te tuatahi me ngā tiakareti i te tuarua nā kua mutu koutou anā [Ākonga 2] whakaatu mai i ō māhere e hia ngā rare?
	Ākonga 2:	Whitu.
	T2:	E whitu? Koirā ngā rare katoa i kōrero a matua e hia ngā rare i hoko i te tuatahi i kī a matua i haere a [Ākonga 1] ki te toa hoko ai e whā ngā rare nē? I kite hoki a [Ākonga 1] e toru ngā tiakarete pai ki a ia, nā reira, i hoko ia i ērā rare e toru, nā reira, e hia katoa ngā tiakarete i a [Ākonga 1]?
	Ākonga:	Whitu.
	T2:	E whitu, nē?
	Ākonga:	Āe.
	T2:	Nō reira, anei e whā ngā rare i a [Ākonga 1] i te tuatahi, e toru ngā tiakareti ka tāpiri ngā rare ki ngā tiakarete ka?
	Ākonga:	Whitu.
	T2:	Ka whitu, ka pai.

The teacher asked very restricted questions about the addition of four and three. At each point, the students responded whitu. The teacher then elaborated on these responses to reinforce the idea of katoa (altogether) and to illustrate the problem with buttons, so that the students could see how the two parts made the whole. He then used this strategy in later lessons to support students counting on from the larger number.

After modelling how a new term or skill is used, having students repeat the action
The teacher often showed students how to make use of a new aspect of the mathematics register in a mathematics activity by modelling for the students before having them do a similar problem.

	T5:	Pēhea tēnei [writes $120 on paper] e hia ngā 10 taara?
	Ākonga:	Rua tekau.
	T5:	Rua tekau?
	Ākonga:	Tekau mā rua.
	T5:	Tekau mā rua. Ka pēhea koe e mōhio ai ko te tekau mā rua te mea tika?
	Ākonga:	Nā te mea he ōrite ki tēnā [points to paper].
	T5:	Āe, he aha ngā mea ōrite?
	Ākonga:	Nā te mea ka kaute i ngā tahi me ngā rua.
	T5:	Pērā, āe he aha ō whakaaro, tama?
	Ākonga:	( )
	T5:	I pēhea koe i mōhio ai ko tērā e 2 ngā 10 i tērā nama mēnā i kī mai 2 ngā tekau i roto ngā tekau taara. Pēhea koe i mōhio ai [Ākonga 1]?
	Ākonga 1:	I kite au i te nama i mua.
	T5:	I kite koe te nama i mua. Tērā te take koinā anā ka whakaatu mai [gets 2 cards to show students the concept] ko te take, titiro e rua ngā tekau ka rua tekau. Ka pai. Titiro [places down 6 cards] tahi, rua, toru, whā, rima, ono. Ngā tekau, rua tekau, toru tekau, whā tekau, rima tekau, ono tekau, mēnā i ki mai ia mēnā 60 tērā [lays another 6 cards beside the others] tahi, rua, toru, whā, rima, ono, whitu, waru, iwa, tekau, tahi, rua. Tekau mā …?
	Ākonga:	Rua.
	T5:	Āe. He aha tēnā nama? [writes number on paper] Ākonga 1 e hia ngā tekau tāra i roto i tērā nama, he ngāwari he ngāwari he ōrite ngā mea katoa.
	Ākonga 1:	Rua tekau mā toru.
	T5:	Rua tekau mā toru. Pēhea koe i mōhio ai?
	Ākonga 1:	I kite au.
	T5:	Nē i kite koe.
	Ākonga:	Āe.

In this extract, the teacher was emphasising the role of the tens column in numerals. He wanted students not only to be able to see this relationship using $20 notes but also to be able to explain it. Consequently, although he accepted a student’s response of there being 12 tens in 120, he wanted this expanded (I kite au te nama i mua). He therefore modelled an explanation before having another student answer a similar question. However, this student’s response to how they got their answer did not provide any more detail than the earlier student.

Recording in writing what had been discussed or done
At the intake stage, the teacher can encourage students to use writing as a way of consolidating new language or the new meaning of terms. Writing is also another mode of communication with its own conventions. Combining knowledge of the new aspects of the mathematics register with knowledge of writing is something that must also be learnt if students are to become fluent users.

In the Evaluation of the Te Poutama Tau 2002, Christensen (2003) found that “[n]one of the teachers recognised that allowing students to develop ways of recording their [numeracy] strategy use might help their thinking, their own and teacher review of strategy use, and their communicating of mental processes” (p. ?). He had recommended that this be emphasised more in the programme.

It, therefore, was very interesting to find that this was being done at this kura. The following extract was in a lesson on halves and the teacher wanted to have students learn ways of finding two even groups or half of an amount. The teacher had asked how many groups 36 could be divided into evenly. After examining groups of five, one student suggests two groups. T6 then asked them to work it out.

	T6:	Ko tēnei te mahi whakarau rua, nō reira, e rua whakarau. Kāore koe i te mōhio e hia ka aha kei te pai me mahi koutou anā?
	[Girl counting with hands.]
	T6:	He tika āu rōpū e rua. Nō reira, kua tīmata koe te nama. Mahi koe i te hāwhe [student coughs] i te wā kua hāwhe koe i te …?
	Ākonga:	Waru, tekau.
	Ākonga:	Kei te mōhio au.
	T6:	Nō reira, ka mahi te aha kia āwhina i a koe? Engari, kei te kī koutou. Āe, he tika tēnā engari, ko ēn- :[cough]: ka taea te uru i te katoa o tēnei nama ki ngā whakarau e rua nērā: [cough]: he aha te hāwhe o te toru tekau mā ono?
	Ākonga:	Iwa.
	Ākonga:	Waru.
	T6:	E iwa tāpiri e iwa ka …?
	Ākonga:	Waru.
	T6:	E waru tāpirihia te waru ki te waru ka tekau mā ono.
	Ākonga:	Tekau mā waru.
	T6:	Tekau mā waru pēhea te (kōpae).
	Ākonga:	Tekau mā waru.
	T6:	Na taihoa, tekau mā waru tekau mā waru tāpirihia te tekau mā waru e waru tāpiri e waru ka …?
	Ākonga:	tekau mā (waru).
	Ākonga:	[Boy points to T6’s paper.] Puritia te ono kei raro.
	T6:	Te ono kei raro.
	Ākonga:	Tāpiri i te tekau mā waru anā ka um tekau mā tahi ki te tahi anā ka toru tekau.
	Ākonga:	Me tiki au he pepa anō.
	T6:	Nō reira, e rua whakarau …?
	Ākonga:	He tekau mā waru.
	T6:	Tekau mā waru.
	Ākonga:	Ka toru tekau mā ono.

One student used her fingers to model the answer while another student started to use blocks. Other students drew in their books. None of the students were successful in working out what 36 divided into two groups would be. A student offered eight and ten as possible answers. The teacher reminded students that they knew what 9 + 9 and 8 + 8 are equal to. Another student then offered 18. The teacher then modelled how writing down 18 + 18 could help them in checking the correctness of this solution. Several of the students supported this explanation.

Students can query obvious errors by the teacher or another student
This did not happen often, as the students were still at an early stage of learning the language. However, there was one occasion when the students recognised that the teacher had made a mistake in her description of an equation, without actually being able to provide the appropriate response themselves.

	T6:	He whakaaro ano, e hia ngā makimaki?
	Ākonga:	E rima.
	T6:	E rima, tekau mā rima whakawehe e toru ka toru.
	Ākonga:	Kāo, he tekau tēnei.
	T6:	Arohamai, kei te tika koe. Nō reira, tīmata. Me mahi whakawehe ināianei maumahara he nērā ana hōmai te whakawehe Ākonga 1?
	Ākonga 1:	Um.
	T6:	E rima ka …?
	Ākonga:	Ka toru.
	T6:	Ka toru.

While discussing the problem of the 15 bananas shared between the 5 monkeys, T6 inadvertently stated that tekau mā rima whakawehe e toru ka toru (15 ÷ 3 = 3). A child queried her about the statement, but suggested that the answer should be 10. The teacher then revisited the problem.

Integration

At this stage, the students would be using new terms and expressions fairly consistently. However, it is likely that if the students are struggling with the mathematics concepts, then they could revert to more familiar terms. The teacher’s role, therefore, has become one of supporting students to keep using the new language even when they are expecting the mathematics to be difficult. The strategies show that the teacher anticipates that students will be able to use the new aspects of the mathematics register, but they may need to be reminded of what they know. At both this stage and the output stage, the students are the ones who are expected to be the main users of the mathematics register. Au (1980), in considering the cultural appropriateness of participation structures in a reading lesson with Hawai’ian students, commented on the ways that students were responding in class. She stated that:

Although the content of their answers is often restricted to teacher-chosen topics, the form of their responding, including many types of joint performance, is much less restricted. A child may reply independently of other children, receive help from others, and comment on, contradict, or complement the answers of others. (p. 111)

Many of the strategies that are used by teachers in these last two stages of the Mathematics Register Acquisition model can be seen as supporting students to be comfortable to respond in a similar range of ways.

Mousley (1999) reported that many mathematics educators believe that students who understand mathematical concepts are likely to be able to: talk about them; explain them; make links between them; apply them across contexts; and represent them. By contrast, students who are restricted to one mode of communication are likely to be weakened in their development of skills and concepts (Ellerton & Clements, 1996). This stage helps students to consolidate their movement between different modes of communication.

This stage is important as it emphasises for students the value of being able to use appropriate language to discuss and describe what they are doing. Gibbons (1998), in studying students’ acquisition of the English register associated with a science topic, found that “as the discourse progresses … individual utterances become longer and more explicit, and this occurs as the students begin to formulate explanations for what they see” (p. 109). Gibbons suggested that teacher requests for explanations is what triggers students to move from the “doing” to the “thinking” in their learning. It is at the integration and output stages of the Mathematics Register Acquisition model that students would be expected to provide these extended explanations through requests by the teacher to think before they speak, encourage students to contribute to others and the teacher, and prompt for more details.

Using commands and linguistic markers to highlight for listeners that they need to pay extra attention to what they are hearing and doing
Listening is a skill in which students need to become fluent in the mathematics register. At this stage of the learning process, students just need to be reminded that they do have good skills in this area and that they should be making use of them. In the following discussion, the teacher seemed to be predicting that some students would struggle to follow the logic so she used words and commands to ensure that they paid full attention to the important sections.

	T1:	Tekau ngā tapa, tekau ngā mata me ngā akitu, tekau mā rua ngā tapa tapirihia kia rua, ā, ka tekau mā rua kē tērā. He oi anō, i mutu i te karaehe i kī mai kē tētahi; “Whaea kei te hē tētahi o ngā mahi, me kī ngā kaute, kua hē tētahi o ngā wāhanga.” Ko [Ākonga 1] tērā, he aha tāu i kite ai?
	Ākonga 1	E waru ngā tapa?
	T1:	E?
	Akonga 1:	Waru ngā tapa.
	T1:	Me whai kē mehemea kei te tika ia. Tahi, rua, toru, whā, rima, ono, whitu, waru, nā reira, kāore ko te tekau! Nā reira, kei te tika te maha o ngā mata me ngā akitu?
	Ākonga:	Āe!
	T1:	Āta whakaaro koa!
	Ākonga:	Āe!
	T1:	Āe, i te mea he aha tētahi atu huarahi i kite kē?
	Ākonga:	Tapirihia te rima ki te rima?
	T1:	Nā reira, kei te kōrero, i rongo koe, koutou i a ia e kii ana? Kōrero mai anō koa, tama.
	Ākonga:	Tapirihia te rima ki te rima?
	T1:	Tapirihia te maha o ngā mata ki te maha o ngā akitu, kua puta kē ko te tekau, nēhā? Te maha o ngā tapa me kī waru ināianei, he aha te huarahi e whai ake? Āe!

This was part of a discussion of how Euler’s rule (Vertices + Faces – Edges = 2) worked on a pyramid and how some of what had been discussed on the previous day had been incorrect. The kē highlighted for the listeners that they should notice and be surprised by what follows. It, therefore, acted as a scaffolding device for students’ listening. They needed to listen so that they could understand the differences between what had been said on both days. This was further emphasised by the teacher with the command “Āta whakaaro koa!” which was to understand carefully and occurred a few turns later. Once the student had responded to the initial question, the teacher emphasised that the students needed to listen. She then had the student repeat what he had said. All of these examples suggest that the teacher was confident that the students would understand what was being discussed, but because of its complexity, she needed to remind them to be careful so that they would not miss the information.

Encouraging students to make contributions to the teacher and to each other
This strategy is similar to the one at the noticing stage, where the teacher’s role is to provide an appropriate context for the new language to be used. However, in this integration stage, as with the final stage (the output stage), the emphasis is on the students using the new language because the context demands it.

	T6:	Me pēhea koe e mahi, āe. Tēnei tikina o mea hei aha te tuhinga i te tuatahi, [coughs] pai tēnei ana me pēhea koe ka whakawehe e ono anō.
	Ākonga:	Kei te mōhio au.
	T6:	Pēhea koe e mōhio kei te tika koe [folds arms, observes students].
	Ākonga:	Kua mahi au.
	T6:	Āna taihoa, āta whakarongo anō kua tīmata mātou (…)?
	Ngā ākonga:	Toru.
	T6:	Nē.
	Ākonga:	Ono.
	T6:	E ono ngā tapawhā i kī atu au ki a koutou tapirihia atu. E ono anō ngā.
		Tapawhā ki ēnei ana awhi atu. E ono anō ki ēnei āe kua mahia ināianei mahia tētahi mahi whakawehe ki ēnei, mahia, mahia. Hei aha te tuhi, mahia kei te awangawanga ētahi o koutou? He moumou wā kia tuhi mehemea kāore koe i te tino mārama i te tīmatanga i ahau ērā rōpū e rua nērā i tāpiri atu au e ono. Anō ki ērā rōpū, e rua ināianei māku e mahi he mahi whakawehe, ka pai. Ka taea e koe te mahi he mahi whakawehe i ēnei mea e hia te katoa o ngā tapawhā ināianei.
	Ākonga:	Tekau mā rua.
	T6:	Tekau mā rua, nō reira.
	Ākonga:	Tekau mā rua whakawehe toru ka whā.
	T6:	Āna he whakawehe anō.
	Ākonga:	Āe, tekau mā rua whakawehe e ono ka rua.
	Ākonga:	Kāo, whā.
	Ākonga:	Kāo, tekau mā rua whakawehe whā.
	T6:	E whā.
	Ākonga:	Ka toru.
	T6:	Ka toru. Āe, te whakarau aha?
		Ākonga:	Whā.
	T6:	Te whakarau toru, me ngā whakarau whā he mahi ano? He whakawehe ano me mahi koutou. Nā i ki mai koutou tēnei tētahi Āe tika tāu i kī mai tētahi ko tēnei āe nō reira he mahi whakawehe ano?
	Ākonga:	( )
	T6:	Āe, kua mahi kē he whakawehe anō.
	konga:	E toru ngā whakawehe mō tēnei.
	T6:	E whā ngā whakawehe mō tēnei. Anā i te whakaaro pai ētahi i te whakaaro, āe. Nā mehemea i a koe tēnei homai te whakawehe.
	Ākonga:	Tekau mā rua whakawehe ono.
	T6:	Ka …?
	Ākonga:	Rua.
	T6:	Ka rua [Ākonga 1], he whakawehe anō?
	Ākonga:	Tekau mā rua whakawehe toru ka whā.

The teacher’s role was one of providing the activity and supporting the students’ efforts to describe what they were doing both to her and to each other. It was quite clear that the students have taken on much more of the responsibility for the discussion. The teacher moved students away from writing down equations around the division of 12, to having the students first model the number sentences with the blocks. The students then offered different suggestions. Both other students and the teacher commented on the suggestions.

Reminding students to think about what they already know
At this stage, if students begin an inappropriate response, a teacher will try to steer them into using new ideas and language by reminding them of what they already know and can draw on in their responses.

	T5:	Āta whakarongo. Pēhea kei a matua toru tekau ngā rare? Ka pai, toru tekau ngā rare i hoatu au. E hia ngā rare, kāo, koa. I hoatu au tekau mā rua ki ōku whanaunga, e hia ngā mea e toe ana?
	Ākonga:	Tekau mā waru.
	T5:	Ko tēnei te tekau kōtiro, tekau rua i kōnei, kōtiro taihoa, kōtiro he aha kōnei nē tekau tangohia rua ka waru nē, ka pai kei au tekau mā waru.

The teacher gave the students the problem of from 30 lollies, 12 are given to a cousin, how many are left. A student arrived at the correct answer using the abacus. She started with three rows of 10 beads and then moved back one row of 10 and two more beads. She then individually counted the remaining beads. The teacher reminded the student that the beads came in rows of 10 so did not need to be counted individually. He also reminded her that she already knew what was added to two to make 10.

Asking a student to repeat a good response
This was seen in the first extract in this section where T1 used e? to get the student to repeat his correct response. Later in the same extract, she specifically asked a student who gave a good response to repeat it (Kōrero mai anō koa, tama). This reinforced for the speaking students the appropriateness of what they had said and suggested that the teacher felt that the students needed this affirmation. It also clarified for other students, who may have been at earlier stages in their learning of the mathematics register, what were appropriate responses.

If a slight correction is needed, the teacher repeats the response correctly
In many of the classrooms, students give answers that are almost correct. Rather than correct the student, the teacher repeats the answer, but correctly. This suggests that the teacher is reminding students of what she feels they know rather than providing new information. A very common error was to give a numerical answer that was not preceded by an e.

	T3:	Me maumahara koutou i tēnei tau?
	Ngā ākonga:	Iwa.
	T3:	E iwa.

The teacher had a series of cards from which she asked students to read the numerals. When a student gave a correct response but failed to include the e, the teacher just repeated the response with the e included.

Summarising what a student has said
Another strategy that teachers use for reinforcing that students have used the mathematics register appropriately is to summarise what the students say. In some ways it would seem that the students are fluent and, therefore, this should be considered part of the output stage. However, at the output stage, it would not be necessary for the teacher to summarise as students would know that they had complete control of these aspects of the mathematics register.

	T7:	He tāpiri, nō reira, kāore i te patu i te tāpiri?
	Ākonga:	Tango, ka huri ki te whakawehe.
	T7:	Tango nā ka huri ki te whakawehe.
	Ākonga:	Ka tangohia te “k” ( ).
	Ākonga:	( ) whakawehe.
	T7:	Mehemea kia noho ko te “k” anahe mehemea ka pērā kei te mahi ngā taha e rua Ākonga 1?
	Ākonga 1:	Me whakarau.
	Ākonga:	Tāpiri.
	T7:	Engari, ko te mahi tuatahi ko tēnei he aha te mea hei patu ko te tango?
	Ākonga:	Ko tērā ( ).
	T7:	Nā whakaarohia, kua huri noa iho kua hurihia ngā mea e rua whakaaro, mehemea kei ahau ono ana kei te tangohia te rua torutanga anahe he aha kei te toe ki au. Mahia kei roto nei: [points to his head].
	Ākonga:	Whā.
	T7:	Kei te karanga noa.
	Ākonga:	[Raises hand.] Rua.
	T7:	Rua.
	Ākonga:	Āe i te mea rua torutanga, nō reira, toru, rua ā kei te tangohia ( ) ka ono ka tini noa e rua.

In T7’s lesson on the y-intercept (k), the teacher reminded the students that they knew how to undo addition. A student suggested subtraction and then factorising (whakawehe). The teacher repeated what the student said and another student introduced the relationship to k. The teacher then had the students reconsider the general equation of a straight line and how they could determine k. Students offered a series of suggestions. The teacher summarised these, but used the numbers from a point and the gradient so it became a specific example.

If a slight correction is needed, the teacher can model doing the action so that the student self-corrects their own response
Sometimes, to remind students that they have got the knowledge and skills to successfully respond to an activity, the teacher repeated an action. In this way, the students recognised what they did inappropriately, and if they are at the integration stage will be able to determine the correct response.

	T2:	Nō reira, e hia katoa ngā pene?
	Ākonga 1:	Ah.
	T2:	Kautehia.
	Ākonga 1:	Tekau mā rima.
	Ākonga 2:	Tekau mā rua.
	T2:	Tekau mā rima? Tekau mā rua? Anā kaute mai koutou.
	Ngā ākonga:	Tahi, rua, toru, whā.
	T2:	E hia ki kōnei?
	Ngā ākonga:	Waru.
	T2:	E waru nā reira ka timata tātau i te waru nē, e hia?
	Ngā ākonga:	Waru, iwa, tekau, tekau mā tahi, tekau mā rua, tekau mā toru.
	T2:	Tekau ma toru.
	Ngā ākonga:	Āe, i tērā nama.
	T2:	Ka pai. Āna, ka mahi tātau tū tahi anō. Kia māu pai i roto i a tātau īra mahi.
	Ngā ākonga:	Tekau mā toru.

In this extract, the teacher was concentrating on Ākonga 1, who was struggling to work out 8 + 5. When Ākonga 2 gave an incorrect answer, the teacher drew the whole group together and asked them to count. When they did not count on from 8, he reminded them of how many buttons there were in the largest group and that they could count on from this. The students counted to 13 and the teacher reinforced both the answer and how they worked out what to do. This interaction showed some features of the intake stage, with the teacher providing a lot of input. However, Ākonga 2 in particular was able to do the necessary calculations using a counting on strategy. The teacher’s role was to remind the students that he was able to do this.

Prompting in a general way for more details
Several teachers would ask students to elaborate on their responses, including asking for their reasons for the action they had just carried out. Although teachers often assumed that a correct answer showed appropriate understanding, queries about the students’ reasoning can be considered as a way for teachers to check up that these assumptions were correct. Barnes (1992) described a classroom situation in which the teacher asked a series of prompting questions that forced students to provide a more detailed description of their understanding of a scientific principle. These questions were not like leading questions that students could not get wrong, but rather they asked the students “to use language differently to break down and restructure [the] area” (p. 73) they were describing. It would seem that the questions asked at this stage in the acquisition of the mathematics register are of a similar nature.

	T7:	Whakaaro, tama, i mua i te kōrero e hia katoa ngā torutanga, mehemea kei a tātou e rima me te tahi torutanga anō ki kōnei, e hia ngā torutanga kei roto i ēnei mea e rima?
	Ākonga:	Tekau mā ono.
	T7:	He aha ai?
	Ākonga:	Nā te mea he ōrite te tahi ki te toru torutanga.
	T7:	Nō reira, toru, ono, iwa, tekau mā rua, tekau mā rima me tētahi atu.

The teacher asked a student how many torutanga (thirds) there were in . The student replied 16. The teacher asked why he thought that and the student stated that there were three thirds in one. The teacher expanded this explanation to show how this made 16 thirds altogether. This expansion may have been done for those students who the teacher felt were still working at a lower stage of acquisition.

Having students write a summary of or record as a diagram what they have learnt
At the earlier stages, the teacher were often very directive about what should be recorded. By the integration stage, students were expected to do their own recording with the teacher just providing reminders about what they already know.

	T7:	Koutou e hiahia ana ahau kia kite i tētahi ruri i ia tangata i ia tangata.
	Ākonga:	He tika ( ).
	Ākonga:	He aha ērā, matua?
	T7:	Ko te pai o ēnei whāritenga, e rua nā kei te kōrero mō te taha tātai koinā te taha tuhituhi nē.
	Ākonga:	Āe pea ka kite.
	T7:	I runga i te tukutuku, ko tētahi kei kōnei ko tērā atu kei kōnei kotahi anahe te wā kei te ōrite. Nō reira, e ai ki tēnei ko- nā he mea nui tēnei waiho wā koutou pene rākau kei raro ruri kei raro tītiro katoa mai ki mua nei: [boy coughs] kei kōnei tēnei wāhi ka tutaki he aha te “t”.

This example came immediately before the final example given in the noticing section. By this stage in the lesson, most students had already written the equations in their own books. The teacher wrote up the two equations before going back to discuss the relationship with the point of intersection.

Facilitating an environment where students will correct each other
As well as having students make evaluations of the appropriateness of suggestions made by their peers and the teacher, at this stage, students can also make useful comments about what is happening if an environment has been set up to encourage this.

	T3:	Āe, mā wai ināianei māhau, ko tēhea o ēnei e whai atu [girl chooses the number 4 card]. Ka pai, mā wai ināianei? Kua mahia koe?
	Ākonga:	Kao.
	T3:	[signals to girl to choose card] Ākonga 1 māu e mahi, e tama, he aha te tau kei muri i tērā? Kōhia. Kei te pai, kāore ia i korā i tērā wā haere ki tērā taha.
	Ākonga 1:	Kāo (… whiua tēnā) [removes the number 9 card placed in error after the 5].
	T3:	Kia ora, e tama, kei te āta tītiro koe ko tēhea. Āta tītiro kei raro kē te rārangi nē, ka pai?
	Ākonga:	Ka pai te kaha [claps].

In placing number cards in order, the Year 0 students in this class often got confused between 6 and 9. Earlier in this lesson, there had been a discussion when the same mistake had been made. At that point, the teacher had provided an explanation. In this extract, a student pointed out the error and described the difference as being the line under the 9. The teacher reinforced this by putting the 6 and 9 cards together. The original student was now able to put the 6 card in place correctly.

Asking students to say whether an answer or term is correct

This was a strategy only used with the youngest students and it was used to support students’ listening skills as it required them to produce very little language. However, this strategy did support students to take on the role of expert. In the extract from T4’s class, the teacher had asked for suggestions on what Little Red Riding Hood would see in the forest. She then had the students evaluate whether the suggestions were appropriate.

	Ākonga:	I kite ia i te kuia.
	T4:	I kite ia i tēnā kuia i te ngāhere?
	Ngā ākonga:	Kāo.
	T4:	[Ākonga 1], hōmai toru, [Ākonga 2].
	Ākonga:	Rau.
	T4:	Rau, he rau i te ngāhere?
	Ākonga:	Āe.
	T4:	Āe, he rau. He mea anō [Ākonga 3]?
	Ākonga:	Kāo.
	T4:	Kāre, i kite he mea he aha ngā mea roa ngā mea teitei nei nā parauri te tinana?
	Ākonga:	Kakī roa.
	T4:	Nā he aha ngā mea kara kākāriki?
	Ākonga:	Rākau.
	T4:	Rākau.
	Ākonga:	Waiho.
	T4:	I kite ia i ētahi rākau [Ākonga 4]?
	Ākonga:	Āe.
	T4:	Hipo.
	Ngā ākonga:	[Laugh.]
	T4:	[Ākonga 2], i kite ia i ētahi hipohipo i te ngāhere?
	Ākonga 2:	Kāo.
	T4:	[Ākonga 5] i kite ia i ētahi hēpara i te ngāhere?
	Ngā ākonga:	Kāo.
	T4:	He raiona?
	Ngā ākonga:	Kāo.
	T4:	Āe, tika tāu ka noho ki roto rā manorito. [Ākonga 1], ki te kore e noho tika hari atu tō tēpu kei muri rā. Ka pai. I kite ia, [Ākonga 2], i ētahi motuka?
	Ākonga 2:	Tērā pea.

This lesson had been on having students use language to do with probability. Therefore, they were practising saying whether Little Red Riding Hood would “definitely see”, “definitely not see”, or “maybe she would see”. By offering her own suggestions, the teacher ensured that the students practised using all terms based on their understanding of what they had heard.

Repeating the question if the students appear to have responded to a different one
This strategy helps to focus students on using their listening skills so that they can respond appropriately, but also reminds them about what the question actually asks them. The teachers use this strategy when they expect that the students to have appropriate knowledge of the mathematics register and the skills to respond in this way.

	T2:	Mai i te rua tekau, kāore, ki te reri?
	Ngā ākonga:	Rua tekau, rua tekau mā iwa.
	T2:	Kei te hoki whakamuri i ēnei rua tekau.
	Ngā ākonga:	Tekau mā iwa, tekau mā waru, tekau mā whitu, tekau mā ono, tekau mā rima, tekau mā whā.
	Ākonga:	Tekau mā waru.
	Ākonga:	Tekau mā toru.
	Ākonga:	Toru.
	Ngā ākonga:	Tekau mā rua, tekau mā tahi, tekau, iwa, waru, whitu, ono.
	Ākonga:	Whā.
	Ākonga:	Rima.
	Katoa:	Whā, toru, rua, tahi, kāore.

The teacher had wanted the Year 0 students to count back from 20. However, they went from 20 to 29. The teacher then reminded them of what the activity was and this time the students responded appropriately. However, some students lost track of their counting at various points and, in the end, the teacher had to complete the counting with the students, which suggested that they may have returned to the intake stage.

Having students complete appropriate actions as they respond to questions
In order to support students moving between different modes of representation, the teacher can often use one mode that they know the students are fluent in to support students’ learning in another. However, the teacher does not provide explicit support, but instead ensures that the students make use of what they can do already.

	T3:	Āe, pēhea tēnā i wareware au i tētahi. Nō reira homai ka noho te tahi kei kōnei te tau kei mua. Kāo, kaua e pā e tū, kaua e nuku me whakarongo noa iho he aha te tau kei mua i te tahi?
	Ākonga 1:	Rua.
	T3:	Kei mua o ēnei.
	Ākonga:	Kore.
	T3:	Kore, kia ora. Āe, ka noho te kore kei mua i te tahi he aha te mea kei muri i te tahi?
	Ākonga:	Rua.
	T3:	Ko te rua ka whai te rua i te tahi, nō reira, ka noho kei muri i te tahi. Hoihoi e tū tama e tū kia tere te haere he aha te tau kei muri i te rua?
	Ākonga:	Toru.
	Ākonga 1:	Toru.
	T3:	Ka pai koe. Waiho ki kō. He aha o whakaaro kōtiro? Me aha ki tēnei tau kore tahi rua a muri kei te whā tatari waiho mā [Ākonga 2]?
	Ākonga 2:	Rima.
	T3:	[Ākonga 3], ki te mahi.

At the start of this extract, the teacher repeated students’ correct answers and as she did so, she placed the numeral cards in a line. When a student gave the correct answer toru (3), another student placed the appropriate card in the line. This occurred again when a student correctly stated whā (4). After a student gave the answer rima (5), the teacher requested another student to now place the appropriate card.

Output

By the final stage in the model, the students use their mathematical language confidently, even in the most challenging situations. The teacher’s role is reduced to providing contexts in which the aspects of the mathematics register will naturally occur. Students’ fluent use of the mathematics register enables them to use that language as a resource for their mathematics learning.

Providing opportunities for students to use aspects of the mathematics register between themselves and with the teacher
The teacher’s role has become one of providing opportunities. Sometimes these opportunities can be very structured and at other times they just arise.

Ākonga:

E rua ngā mea o te kōwhai ki te taha, kotahi te mea kōwhai, oh, e rua ngā whero ki te taha. Kotahi te mea kōwhai o ia huapae.

This extract comes from T1’s fifth lesson, where a student had to describe the arrangement of five blocks to another student. The second student could not see the arrangement and relied entirely on the first student’s description. Many students struggled initially with being able to describe the arrangement of groups of different coloured multi-link blocks. However, it was clear from this student’s response that he had full control of the location expressions and knew how to use them to give a clear description in this activity.

Another example comes from one of T3’s lesson. In this lesson, students were reciting the numbers, from one to nine, in order and placing the corresponding numeral cards in a line. While the teacher was talking about something else to the group, one girl placed a 1 and 0 together to make 10 and put it after the 9 numeral card in the line. This unprompted act showed that this students had good control of the numerals.

Providing an environment in which the students can query the language use of the teacher
When students are fully fluent in the mathematics register, they no longer need to be guided by the teacher about what is appropriate as they can make those judgements themselves. Consequently, they can use this knowledge to query the teacher’s use of aspects of the mathematics register.

	T7:	Mahi kāinga. Kei a koutou te tikanga, mehemea ka tuhi kei runga i te tukutuku kāre rānei, engari, kāre au i te hiahia nē, Ākonga 1, kia rongo kāre au i mahi mahia. Ānei ngā mea e rua oh e rua ngā pātai oh tērā pea, kotahi te pātai mahia tēnei ka tutaki ērā rārangi e rua.
	Ākonga:	Āe.
	T7:	Āe, ka kōrero tere ia kei mua i te whakaaro.
	Ngā ākonga:	Āe.
	T7:	Whakaaro koutou.
	Ākonga:	Kāo.
	Ākonga:	Kāo, kāore.
	T7:	Whakaaro koutou ka timata ki te toru tōrunga whakaurua tahi rua timata kei kōnei tahi rua he rārangi aha.
	Ākonga 1:	Whakarara.
	T7:	Whakarara kāre rawa e tutaki he aha ai i te mea he ōrite te.
	Ākonga:	Te “r”.
	T7:	Kāre te “r” te mea, kei mua i te “r”.
	Ākonga:	Rua.
	T7:	Te rua. He aha te rua, he aha tērā mea?
	Ākonga:	Rōnaki.
	T7:	Te rōnaki, ka pai.

In the rush at the end of a lesson, T7 set homework to find the point of intersection of two lines. A student queried this, saying that the lines were parallel (whakarara). The teacher then used this intervention to ask the rest of the students what was the same in both equations for the lines to be parallel. One student suggested that it was r. The teacher then stated that it was the number in front of the r. A student replied that this was rua (two). The teacher then asked what the number stood for. A student stated that it was the gradient. At least one student was fluent in interpreting straight line equations so that he could query the teacher. However, the series of questions that the teacher followed up with, and some of the students’ responses, suggested that other students were working at the integration stage and maybe even the intake stage.

Effective strategies

Our original research question had been about identifying the effective strategies used by teachers to support students in acquiring aspects of the mathematics register. However, it soon became clear from our analysis that a scaffolding or modelling strategy could not be judged as effective in isolation from the whole lesson or in fact from classroom practices in general. Wells (1999) similarly stated that “in the hands of different teachers, the same basic discourse format can lead to very different levels of student participation and engagement” (p. 169). Therefore, there is a need to better understand the contexts in which the strategies are used, both individually and combined, to support the acquisition of the mathematics register.

Our starting premise was that each strategy was related to a particular stage in the acquisition model. The Mathematics Register Acquisition model is only one way that language learning within mathematics classrooms can be considered and so there are implications for choosing to adopt this way of doing the analysis. What constitutes an effective strategy needs to be considered in regard to its role in acquiring the mathematics register, and the Mathematics Register Acquisition model in particular. A strategy that is effective at the noticing stage is unlikely to be an effective strategy at the integration stage. This is because it would be unable to fulfil the functions of both stages well.

Previous research has tended to focus on dialogical structures in mathematics classrooms, where English was the language of instruction, and their contribution to students’ mathematical understanding (see Nathan & Knuth, 2003; Bill et al., 1992; Moskal & Magone, 2000; White, 2003; Tanner & Jones, 2000). This meant that some structures were criticised or recommended according to this criteria. For example, Wood (1998) criticised the use of leading questions where the student simply provided a one word answer to questions that they would have difficulty getting wrong. She stated that “although the teacher may intend that the child uses strategies and learn about the relationship between numbers, the students need only to respond to the surface linguistic patterns to derive the correct answers”. She suggested that an alternative pattern which she labelled “focusing” would be more effective in promoting learning. “A high level of interaction between the teacher and students creates opportunities for children to reflect on their own thinking and on the reasoning of others” (p. 172).

However, if the interactions are reappraised as being about language learning, then rather than seeing the interaction patterns, such as funnelling and focusing, as being in opposition, it is possible to see how they can both contribute to students’ learning. The example of using sets of leading questions was seen in several teachers” extracts and was firmly conceived as belonging to the noticing stage. It is a scaffolding strategy that supports students to use new terms, meanings, or expressions when they are first introduced. It could not be considered an effective strategy for the integration stage, because at this stage the teacher’s role is to remind students of what they already know and for the students to do the work. At the integration stage, the focusing pattern that Wood (1998) recommended is much more valuable because the cognitive work is done by the student. Many of the strategies at the integration and output stages supported students to use aspects of the mathematics register to communicate their mathematical thinking effectively. It is at this stage that it becomes difficult to separate the scaffolding experiences as one contributing to language learning or to mathematics learning. By this stage in the learning process, mathematical learning and learning the mathematics register are closely intertwined.

As a maximum of five lessons were videotaped for each teacher, it was not possible to identify the strategies that were the most successful in supporting students’ use of new aspects of the mathematics register. That would have required a longitudinal study such as the one undertaken by Gibbons (1998), where examples of both classroom talk and students’ writing were collected and analysed together. What is clear from our data is that there was never one strategy that characterised how a teacher scaffolded language learning when they believed their students to be operating at a particular stage on the Mathematics Register Acquisition model. All of the teachers used more than one strategy when operating at a particular stage. Thus, in considering issues of effectiveness, there is also a need to consider the combination of strategies that a teacher used at each of the various stages. This will be discussed in greater detail later in this section.

Before a description of effective strategies for the acquisition of the mathematics register can be given, it is worthwhile to summarise what the functions are of each of the stages. It is also worth noting that it is clear from the extracts that teachers may use several different strategies at the same time. So at the intake stage, although a teacher may be explaining how to record in writing a mathematical response that had been discussed previously, she may also repeat a student’s response. The reasons for the provision of two types of strategies are two-fold. The first is that the teachers are aware that different students will respond better to some scaffolding and modelling strategies than to others. Thus, it is important to provide a range of scaffolding and modelling strategies to match these different students’ needs. The second reason may also be that, if strategies were used from two different stages, the teacher believed that there were students in the class who were working at different stages of the acquisition model.

In the brief summaries of each of the stages given below, teachers’ suggestions about new strategies that they would try in 2006 are also described. In April 2006, a meeting was held with the teachers and the researchers to discuss the different strategies that had been documented. Two teachers, T2 and T4, were unable to attend this meeting. A new teacher, who had just started at this time, also participated in the meeting. Part of the discussion revolved around the strategies that teachers would use in their mathematical language teaching. As it was felt that videotaping of the lesson later that year would be done by pairs of teachers who had classes of similar year levels, pairs of teachers chose strategies to trial together. The teachers’ choices provide some indication of the strategies that they felt were effective as these were the ones that they wanted to try out. However, because of difficulties with filming at the times planned, there is no evidence of whether the teachers actually tried out these strategies.

Noticing

The noticing stage is when the teachers introduce new terms or expressions or add extra meanings to ones that students are already familiar with. The function of this stage is to make students aware of new aspects of the mathematics register, whether these be new layers of meaning for already known terms or previously unheard terms or expressions. This stage is characterised by the teacher doing almost all of the cognitive work. They engineer the activity so that the new terms are needed. They ensure that the words are used frequently, mostly by themselves, but also by the students. Elley (1989) found that for vocabulary acquisition to occur from listening to stories, and to be remembered three months later, seven-year-olds needed to hear the meaning of the new vocabulary and to hear the word frequently. It would seem that the teachers in this research also felt that it was important, in these early stages of acquiring aspects of the mathematics register, that they ensured that students frequently heard and were guided into using the new aspects of the mathematics register. The Māori teachers in Christensen’s research (2003) felt that the acquisition of new mathematical vocabulary was assisted if they “understood the Māori origin and mathematical context of the word” (p. 35). It may be that the experiences of the teachers in our study in learning vocabulary gave them insights in how to support their students’ learning.

It would seem that for a strategy to be an effective one at this stage, it must contribute to students hearing new vocabulary or grammatical expressions frequently and gaining meaning from them. At this stage, the understanding that students are expected to acquire is usually a definition. However, the teachers giving a rationale also provided another kind of meaning to the new aspect of the register that they were highlighting. By the intake stage, this understanding is developed into a sense of when and how to use the new aspect of the mathematics register.

One pair of teachers opted to provide students with a rationale for what they were learning as one of the strategies to be trialled in 2006. This choice was interesting because both of these teachers taught junior classes. Very few metacognitive strategies for supporting students to become more aware of their own learning had been seen in the 2005 videotapes of junior classrooms. Although no data were collected to show whether these teachers had in fact done this (T8 was new in 2006 and T3 left the kura in August 2006), it is interesting to see that these teachers at least initially viewed this as an effective strategy that they had not used previously.

Intake

At this stage, some of the cognitive load has shifted to the students. They now need to give definitions and examples, rather than just being expected to notice and interpret those provided by the teacher. However, the teacher is still very much in control and students’ contributions are usually short, thus providing them with little opportunity to provide inappropriate responses. The function of the intake stage is for students to form understandings of when and how new aspects of the mathematics register are to be used. Effective strategies, therefore, are ones that support students exploring when and how to use these new aspects of the mathematics register. This support would include providing students with both positive and negative feedback about their experimentation with the new aspects.

Several of the effective strategies that teachers wanted to experiment with came from this stage. Two teachers at the April 2006 meeting wanted to work back with students from a wrong answer to the original question. This strategy can provide students with an understanding of where they may have over-generalised an understanding in an inappropriate way. So, in learning about two digit subtractions, a student may take away a smaller number from a larger in all cases (43–27 becomes 47–23) because of their previous experiences with subtraction. By having a student go back from their answer to the question, not only does the teacher become fully cognisant of what the student has done, but it may be that the student becomes aware of their misunderstanding themselves. Nathan and Knuth (2003) discussed the difficulties that teachers had in reconciling the need to accept all students’ responses (social scaffolding) and the need to ensure that mathematical ideas were central in these responses (analytical scaffolding). This strategy would seem to blend these two needs as a student’s answer is made use of with the student themselves evaluating its appropriateness with support from the teacher.

The two teachers of junior classes wanted to have students give responses visually with materials as well as providing narrative descriptions both orally and in writing. This use of different modes of expression was seen as supporting students’ understanding of how and when they could use the new aspects of the mathematics register as well as gaining a better definition of them. Moskal and Magone (2000) suggested that “[a]lternative modes of representation can provide different insights into the nature of the problem and the solution process” (p. 319). By understanding how meaning is instilled into the wording or the drawing of diagrams, students will gain a better understanding of how to use the mathematics register in solving a mathematical problem.

Two other teachers felt that they wanted to encourage students to provide rationales for what they were learning. These were teachers whose classes were at the middle school level. Having students provide a rationale helps them gain a metacognitive awareness of why they were learning this aspect of mathematics.

Integration

By the integration stage, students have a good understanding of the new aspects of the mathematics register. The function of this stage is to have students use these new aspects, but in a situation where the teacher is able to step in and provide support if necessary. Consequently, the teacher’s role has become one of reminding students of what they know and can do. The students are the ones who have the major responsibility for making use of the language that they have gained. If the student seems unable to operate at this level, the teacher is quickly able to supply more support, thus recognising that the student is still at the intake stage. Effective strategies are, therefore, ones that allow students to have major control of their use of the mathematics register, but enable the teacher to remind students about what they know and can do.

The strategies from this stage that the teachers saw as something they wanted to try were: having students give written responses when the audience was their peers; and providing an environment where students would make contributions to each other and to the teacher. Both of these strategies are about having students become aware of an extended audience whose needs as readers or listeners should be considered. This consideration can then become a metacognitive awareness of what needs to be thought about in order for them to produce a coherent, concise description or explanation. These strategies would also support students’ problem solving abilities (Meaney, 2002).

Output

The final stage of the Mathematics Register Acquisition model allows students to show their fluency in using the mathematics register. Its function is for students to be able to show what they know and can do without any support from the teacher. At this stage, there is not a series of strategies that teachers choose from. The teacher’s role is simply to provide opportunities for students to make use of the fluency that they have acquired. An effective strategy is, therefore, one that supports this provision.

Summary

The criteria for effectiveness in scaffolding and modelling is different according to the function of each stage in the Mathematics Register Acquisition model. There are general features of a strategy that need to be present if the strategy is to be effective in meeting the function of the Mathematics Register Acquisition stage. However, even when strategies had these features, some were considered as being more effective than others.

Having looked at the list of strategies used in the mathematics classrooms at the kura, teachers agreed to trial strategies that they had not used previously. These strategies gave an indication of what the teachers felt were effective strategies. On the whole, these strategies tended to be those ones that supported students gaining a metacognitive awareness about their learning of the mathematics register. They were also strategies that tended to encourage students to move between modes of expression.

Both sets of strategies can be seen as supporting students to become self-regulatory learners, who take on the responsibility for their own learning. Pintrich (2000) defined self-regulated learning as “an active, constructive process whereby learners set goals for their learning and then attempt to monitor, regulate, and control their cognition, motivation, and behavior, guided by their goals and the contextual features of the environment” (p. 453). Gaining metacognitive awareness of their own learning would contribute to students becoming self-regulatory. In discussing the relationship between the individual and their environment in developing self-regulatory processes in classrooms, Meyer and Turner (2002) suggested that there were three ways in which this process was supported by teachers. These were through:

1. helping students build competence through increased understanding
2. engaging students in learning while supporting their socioemotional needs, and
3. helping students build and exercise autonomy as learners. (p. 18)

Many of the strategies that the teachers used, and certainly the ones that they wanted to try, seemed to match Meyer and Turner’s ways. For example, all of the strategies could be seen as supporting students to gain an increased understanding as “[i]nstructional support that negotiates meaning, building a shared understanding of what is known and what is knowable is necessary to promote student competence” (Meyer & Turner, 2002, p. 22). Moving between different modes of expression would contribute to this negotiating of meaning. Promoting a classroom where students offer suggestions to others and to the teacher and query the contributions of the teachers would support students to feel comfortable engaging in vigorous debate about what and how they were learning. Christensen (2003) reported that as a result of involvement in the Poutama Tau programme, most teachers “recognised they could assist students by providing a learning environment where emotional safety was not a cause for students to ‘hold back’ their ideas” (p. 36). In this project, it seemed that facilitating the development of a supportive socioemotional environment where students were comfortable to discuss ideas contributed to students’ learning. Providing students with and having them describe a rationale for their learning would also contribute to students becoming autonomous learners.

Combining strategies

When considered in isolation, some strategies employed by teachers at the various stages of the Mathematics Register Acquisition model could be considered less effective than others. For example, having students repeat an answer, after the teacher has gone through an explanation to reach it, is perhaps not going to highlight for students new aspects of the mathematics register very effectively. However, when this is one strategy of many, all designed to support students to become aware of these new aspects, then it could be seen as having more value.

Appendix B contains a description of T1’s strategies over the course of her five lessons. It is provided because it shows how the focus for learning new aspects of the mathematics register changed over the series of the lessons. Of all the teachers, T1 had the most lessons videotaped and, therefore, was the most value as an example. However, she did seem to be very aware of her language teaching and perhaps was not a typical example of the teachers. The results from examining how the strategies changed across the lessons are discussed in the next chapter. However, in this section, they are worth considering to see how a combination of strategies from the different stages was used in each lesson. In Appendix B, changes in fonts represent the different lessons so it is possible to see how many strategies were used at each stage of the model. When the teacher used the same strategy in more than one lesson, especially if the same aspect of the mathematics register was the focus, then it was often not recorded on the strategy sheets. The strategy sheets in Appendix B simply provide an outline of the range of strategies that were used by this teacher.

The strategies described in Appendix B show that in each lesson, the teacher used a series of different strategies. The exception was lesson five, where the teacher set up an activity in which students described arrangements of multi-link cubes to groups of their peers. This activity provided students with an opportunity to use fluently the location words that they had been learning in previous lessons. It was considered as being an example of a strategy from the output stage. In each of the other lessons, if the teacher used strategies from an Mathematics Register Acquisition model stage, she would always use more than one. Combining a range of strategies, therefore, seems to be part of what makes effective support for students who are operating at the different stages.

Māori scaffolding and modelling strategies

One of the reasons for doing this research was to document the unique practices of these teachers that reflect their approach to supporting students in a culturally appropriate manner. Au (1980) described culturally appropriate instructional events for minority children as those that met three criteria. These were:

1. it would have to be comfortable for the children
2. it would have to be comfortable for the teacher, and
3. it would have to promote better acquisition of basic academic skills. (p. 93)

Although we have some interviews with the students, we do not have sufficient data to determine the strategies that students felt most comfortable with. However, the engagement of the students was obvious in the videotapes. In one of the interviews, a student mentioned that he found describing ideas through writing and talking together very helpful. This supports the point made above about the value of moving between modes of expression, and was something that the teachers also valued.

If teachers used a strategy in their lessons, it can be assumed that they were comfortable to do so. As was discussed earlier, there is evidence that Māori teachers found learning new mathematics vocabulary easier when they knew the Māori origin of the words and understood the mathematical idea that it described (Christensen, 2003). It, therefore, seems possible that the teachers were comfortable in promoting mathematics register acquisition of their students by using strategies that they knew worked for themselves.

The third criteria of Au is one that requires further investigation. In considering the modelling and scaffolding strategies for supporting the acquisition of the mathematics register, it would seem that all of the strategies could be considered culturally appropriate. The question then becomes one of investigating whether there are some strategies that are only likely to be seen in Māori immersion classrooms.

Many of the strategies described in the earlier sections of this chapter would also be seen in English medium classrooms both in New Zealand and in other countries, such as Australia, the

United States, and the United Kingdom. However, the use of the linguistic resources within te reo Māori for scaffolding is one strategy that is unique. Words, such as ara and kē, that warn listeners about the type of material that will follow, are not found in English. Given that Māori immersion education was set up to reverse the decline in Māori language (Spolsky, 2003), there has been a recognition that “the authenticity of the language is maintained” (Christensen, 2003). Concerns have been raised about the possible implications for te reo Māori as a consequence of its use for discussing mathematics (Barton et al., 1998). It is, therefore, interesting to find authentic resources within te reo Māori that can be of value in the teaching of mathematics.

Another feature, although not unique to kura kaupapa classrooms, but that seemed to be more strongly observed in the videotape recordings, was the amount of student contribution to the interactions. This can be seen in the extracts provided in the previous sections illustrating the strategies of each of the Mathematics Register Acquisition model stages. Even at the noticing stage, which is where teachers have the most responsibility for doing the cognitive work, students have an active role in contributing to the discussions.

From watching the videotapes, it was quite clear that teachers were very aware of the need for wait time to ensure that students provided the best possible answer. Tobin’s (1983) review of previous research indicated that extending the wait time in science classrooms resulted in more effective questions and responses by teachers and students respectively. It was suggested that this would result in increased science achievement by students. The use of wait time in the videotapes from this research was just one aspect that highlighted the teachers’ respect for and support of their students as active participants.

In Appendix B, the strategy sheets from T1’s lessons provide arrows illustrating how interactions progress. Each dot point shows the beginning of an interaction. It was quite clear that students originated the interactions as often as the teacher. Even when interactions were not connected to student responses, it was clear that students were often expected to respond. It was just that these responses did not influence the direction of the interaction as they clearly did in the more extended interactions.

It would seem that strategies that reflect a Māori world view are those that use the features of te reo Māori effectively and those that support students to become active participants in interpreting and producing the mathematics register appropriately.

4. The effect of student age on modelling and scaffolding strategies

Progression of learning of the mathematics register

One of the questions that we wanted to answer was whether effective strategies were closely tied to the age of the students. It was certainly clear that the year level that students were in did have an effect on the aspects of the mathematics register that were taught. Discussions held in April 2006, in which the results of the analysis of the teachers’ videotapes were discussed, resulted in the outline of the terms and ideas related to triangles shown in Table 1.

Table 1 Progress on aspects of the mathematics register around triangles

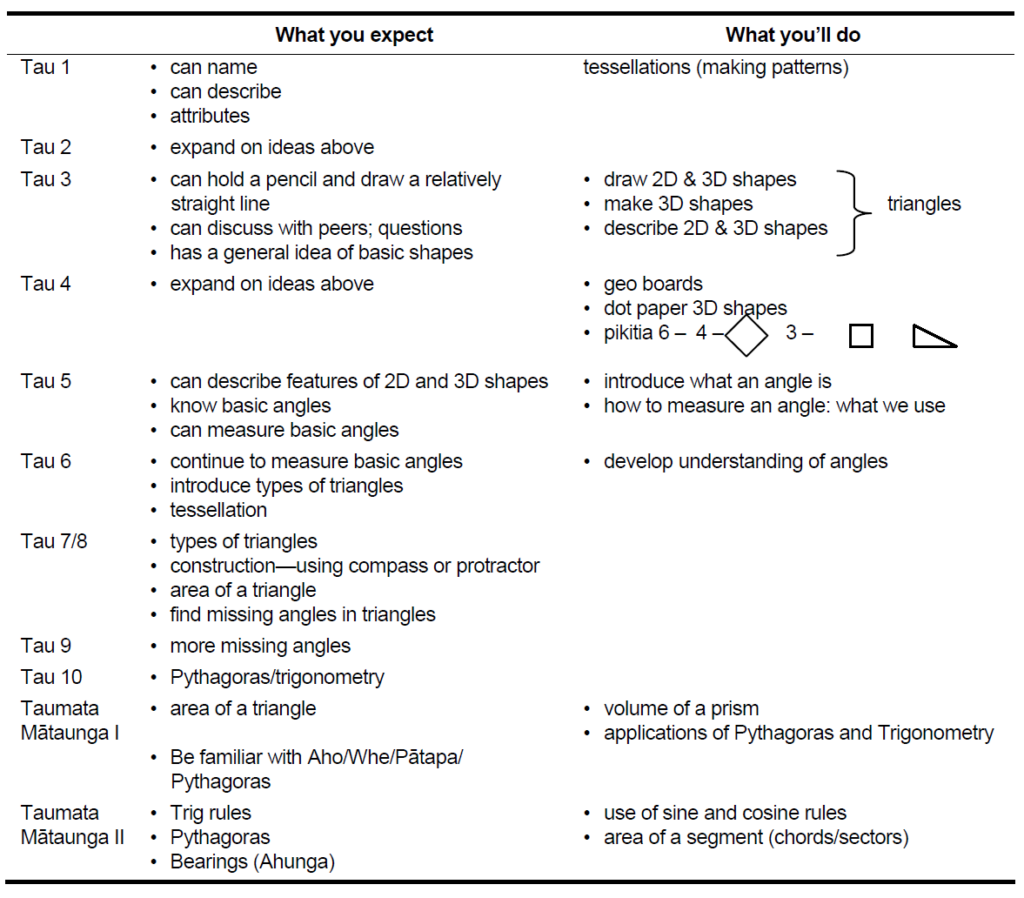
Table 1 showed that there were many aspects of the mathematics register that students needed to acquire in regard to ideas about triangles. These started with being able to recognise it as a shape and being able to name it as a triangle. From there, teachers believed that students needed to be able to recognise and to talk about different features, including angles. The student also needed to draw different triangles and features and use their understandings when providing geometric justifications. The teachers’ discussion about what aspects of the mathematical register students needed to know when they started in a year level and what would be taught was ongoing. The teachers found this discussion useful as it gave them a sense of how ideas and the accompanying language demands developed. Christensen (2003) stated that “[i]f students are introduced to the specialised vocabulary relevant to their level, they will experience less difficulty when further terms are added as they move to higher levels” (p. ?). Discussions, such as the one that resulted in Table 1, will contribute to the kura having a cohesive understanding of the mathematics register that students would be expected to know and to learn at each year level.

At a further meeting in August of 2006, there was more discussion about when to move from students’ everyday language into using specific aspects of the mathematics register. Teachers were also concerned about when it was appropriate to use students’ or classes’ idiosyncratic expressions and when these needed to be changed into standard mathematical terms. Teachers felt that there was benefit to even young students in being consistent in using vocabulary throughout the school. In the research by Christensen (2003), concern had also been raised about the use of “local school dialect” instead of the standard terms because of the high mobility of students in Māori immersion schooling. The teachers in the current research felt that being consistent would provide students with a database of words that could be built on from year to year. There was a sense that, even at Year 1, students may only have a limited linguistic repertoire of te reo Māori to draw upon. Consequently, there was a need to build up this base through concerted effort. The teachers suggested that a word bank be developed so that the word usage across the kura would be consistent.

However, there was a recognition that standardising the language too quickly was not appropriate, as filtering nonstandard terms from students’ repertoires could be restrictive in the meanings that they were able to develop. The use of alternative terms was not always considered inappropriate. Sometimes there were no alternatives and so there was little choice about the terms that should be used. At other times, there were acceptable alternatives. Examples of these were nama, tau, tāpiri, and tao. In English, there are often two or more terms that have the same meaning and being able to use both gives students insights into the relationships between different ideas. As a consequence of this discussion, the teachers recorded these aims for the progression of mathematics register acquisition:

• want to have a base language
• do not want to limit it
• extend their language as they go
• have clear progressions
• ensure consistency.

Christensen’s (2003) research had highlighted the need for consistency in te reo tātaitai across the Māori immersion schooling sector and across year levels. Through their discussions during the research project, the teachers at this kura reached an understanding about the tension between the need to support students’ learning through providing consistency in vocabulary use and the loss of fluency that could result if this standardisation occurred too early. As was done with the topic of triangles, these discussions also resulted in ongoing development of progressions about the acquisition of mathematics register.

Scaffolding strategies and year level

It would seem that there is a sense of the progression for acquiring aspects of the mathematics register across the kura. This progression is quite clearly related to the year level of students. However, the relationship between the strategies that teachers used and the year level that they taught was much less clear. As the teachers only videotaped a maximum of five lesson, there is not enough data to be able to tell which strategies had the greatest effect on students’ acquisition of the mathematics register. However, it is possible to describe those strategies that appeared to be related to the year levels that students were in. It must be remembered that strategies captured in the videotaped lessons do not represent all of the strategies that each teacher might employ. Factors such as the topic of the lesson and how new the material was to students in the videotaped lessons did influence the teachers’ choice of strategies. Table 2 shows the strategies that were used by two or more teachers. It also indicates which of these strategies were used by teachers at the different year levels. On the whole, most strategies tended to be independent of age.

At the noticing stage, writing the new term in an equation and using fill-in-the blank sentences were the only strategies used by teachers from just one area of the kura. The first of these strategies was only used by the teachers working with students in later years of primary school. However, given that students need to learn how to write mathematics symbolically at all year levels, it is unlikely that this is, in fact, an age-dependent strategy. It is more likely that it was the choice of the lessons to be videotaped that resulted in this strategy appearing to be used only by teachers of this age group. The second strategy, where teachers began a sentence that students were then expected to finish, was used only by the teachers of the older students. Once again, it is difficult to accept that this is an age-dependent strategy. It forms part of a teacher–student exchange that has been documented in a number of classrooms and is known as the IRF (initiation—response—feedback) exchange (Mehan, 1979). The teacher asks a question by leaving the sentence unfilled. The students are expected to provide the response and then the teacher would provide either explicit feedback, through affirmation or negation of the response, or indirect feedback by asking a new question. It seems unlikely that this is a strategy that only teachers of older students would use.

At the intake stage, the teachers of the older students were the only ones to use specific amounts to illustrate a general rule. The restricted use of this strategy is most likely to do with the introduction and use of algebraic equations that these students are working with. The relationship then between general rules and specific amounts is unlikely to be so important in the earlier grades. This, therefore, may be a strategy that could be considered to be age-related.

The two teachers teaching the intermediate and high school mathematics classes were also the only ones to use commands and linguistic markers as a scaffolding strategy to encourage students to make use of the language skills and knowledge that they had. It is difficult to know whether this is an age-related strategy. It would seem that, in order for students to take advantage of linguistic markers, they must have good skills in everyday te reo Māori. It may be that this knowledge comes later in the acquisition of te reo Māori and, therefore, is not available to young students. However, more research would be needed to confirm this.

It may also be that commands, such as to listen carefully, are useful to older students. This is because students need to have the knowledge to interpret these commands as ones that suggest that they have the skills and understanding to make use of the information available to them. Younger students may need more explicit directions about what they are expected to do, especially when the activity that they are working on is made up of several components.

The output stage contained no strategies that were used just by teachers of one age group of students.

In summary, the overwhelming impression from Table 2 is that there were almost no strategies that seemed to be related to the year level that students were in. The possible exceptions for this would be the strategies of illustrating a general rule with specific amounts and using commands and linguistic markers. However, given the limited number of videotaped lessons from which the data were collected, it may be that even these two strategies are used by teachers of younger students.

Table 2 Strategies used by teachers of different student year levels

	Junior Primary			Rest of Primary		Intermediate	High School
	T2	T3	T4	T5	T6	T1	T7
Noticing
providing opportunity	√		√	√	√	√	√
using intonation	√						√
repeating new terms and expressions			√		√	√
rephrasing the expressions					√	√
writing the new term in an equation				√	√
giving definitions				√		√	√
emphasising the relationship between ideas	√			√	√		√
modelling a new term or skill	√			√
using a set of leading questions	√				√	√
using fill-in-the-blank sentences						√	√
Intake
students do choral responses	√	√		√
asking students for definitions					√	√	√
having students model use of terms	√			√		√
asking students for examples of a term	√					√	√
having students draw or use materials	√			√	√		√
repeating appropriate responses	√	√		√	√	√
elaborating on students’ responses	√			√	√	√
asking further questions	√			√	√	√
having students provide a rationale					√	√	√
querying inappropriate responses					√	√	√
illustrating a general rule with amounts						√	√
focusing back onto the main idea	√						√
relationship to new language	√	√			√	√
answering a series of closed questions	√				√	√
having students repeat the action	√	√		√
recording in writing	√				√
Integration
using commands and linguistic markers						√	√
encouraging students to contribute	√		√	√	√	√	√
reminding students to think				√	√	√	√
summarising what a student has said				√			√
prompting for more details				√	√	√	√
having students write a summary				√		√	√
facilitating an environment where children will correct each other	√	√					√
asking whether an answer is correct	√		√	√
repeating the question	√	√				√
having students complete actions	√	√			√
Output
providing opportunities	√	√	√		√	√	√
students can query the language use of the teacher			√			√	√

The effect of the newness of the topic on strategy use

If the age of students does not have a strong effect on the strategies used, was there anything else that seemed to influence teachers’ choice of strategies? The answer would seem to be the newness of the topic. It would seem that when the topic has just been introduced, then the strategies tend to be from the noticing stage. As the unit of work continued, the strategies tend to come from the later stages. The main point that comes from this investigation is that a balance of strategies is needed for new aspects of the mathematics register to be acquired by students.

T1’s strategies are presented in Appendix B and provide the basis for looking at this issue. Although none of the other teachers recorded five lessons, the lessons that were recorded also seemed to fit this pattern. If T1’s strategies, presented by the Mathematics Register Acquisition stage in Appendix B, are considered, it is possible to see how strategies are grouped in different lessons. This grouping can be seen through the use of the different fonts to highlight what was done in various lessons. For example, noticing strategies were only used in lessons 1, 2, and 4. At the intake stage, there were strategies from lessons 1, 2, 3, and 5. Strategies from the integration stage were used in lessons 1, 2, 3, and 4. The output stage’s strategies came from lessons 1, 2, and 5. This would suggest that there was not a clear pattern. When this pattern is considered further, the complexity of the situation is revealed.

The topic for this unit of work was one of having students become aware of the properties of the arrangement of cubes as part of a larger unit on three-dimensional shapes. The beginning of the first lesson that was categorised as being part of the output stage was related to commentary on the previous lesson. A student queried the teacher about what had been written up on the board at the end of the last lesson. The strategies from the integration stage in this part of Lesson 1 are concentrated on having other students gain the most understanding from the confident student’s explanation. Although this student was operating at the output stage, the teacher seemed to believe that some members of the class were operating at an earlier stage. She cued them into listening carefully through the use of linguistic markers, but also used rephrasing and fill-in-theblank sentences to introduce vocabulary. Concurrently, she went over students’ knowledge of three dimensional shapes by having them provide examples.

In the rest of the lesson, the teacher introduced ideas about the faces that are on cubes. She had put dots on each face and then placed several cubes together. The aim for this part of the lesson was for students to use an equation to work out the number of dots that could be seen. The majority of the time was spent in the teacher explaining how to work out the number of dots. To do this, she used a series of questions that led the students to understand what was required. She then had students work on different arrangements of blocks and then provide explanations of how they worked out the number of dots. The teacher then used this to introduce the whāritenga (equation). If the aim of the lesson was to develop and then use the equation, then it is understandable that the majority of the lesson revolved around strategies from the first two stages. The use of strategies from the integration stage encouraged students to make use of the skills and understanding that they already had to support them in recognising when an equation was appropriate and how to use it.

Lesson 2 also continued with identifying the number of dots, but the aim was for the students to be able to give clear explanations of how to do this. Although there were still strategies from the first two stages being used in this lesson, most of the lesson concentrated on having students provide these explanations. The strategies from the earlier stages were used to ensure that the students were familiar with terms such as huapae and poutū that were needed to give the explanations. In this lesson, students were also expected to draw sketches of their block arrangements and, thus, provide a written description of their experiences.

The emphasis in the series of lessons shifted from “learning” to “using” aspects of the mathematics register around the arrangements of blocks. Consequently, the majority of the time in the lessons changed from introducing new terms and expressions to fluently using them. Lessons 3 and 4 continued this shift, and lesson 5 was based on an activity in which the students were expected to provide complete descriptions of block arrangements to their peers. It was the feedback from their peers that made it clear to the speakers whether they had been successful or not.

It would seem that when a new topic is started, there is a concentration on introducing new aspects of the mathematics register. However, there is also a need to ensure that there are opportunities within each lesson for students to use those aspects of the mathematics register that they have fluency or near fluency in. This fluency can be used by them in acquiring new aspects. This is because it helps students to connect the new information to what they already know and gives them an understanding of the contexts in which the new aspects would be relevant. Acquiring the mathematics register involves students gaining fluency in being able to speak, listen, read, and write it. Moving between strategies, from different stages, also shows how a teacher uses the students’ ability in one language skill to support them gaining fluency in another skill.

Therefore, there is a relationship between whether a topic is new or not and the most common strategies that a teacher uses in scaffolding and modelling the mathematics register. However, it is appropriate that strategies from later stages of the Mathematics Register Acquisition model are also seen in each lesson. This is because students need to keep using what they already know about the mathematics register or, like a second language learner who is not regularly using their second language, they may lose fluency. It is also important that teachers use strategies from the later stages, because having skills and understanding of one aspect of the mathematics register is an important resource for learning new aspects.

5. Effect of the research on teachers’ practice

The final research question was about the effect that learning about different scaffolding and modelling strategies of aspects of the mathematics register had on teachers’ practices. Comments by teachers in surveys and interviews done at the completion of the project suggested that being involved in this research had an effect on their teaching of mathematics and, in particular, their teaching of aspects of the mathematics register. Analysis of the use of mathematical and nonmathematical words repeated more than seven times showed that teachers of junior classes increased the proportions of mathematical words in the second year of the project.

Reflection-in-action

Teachers were actively involved in the collection and analysis of the data. Through videotaping and analysing their own lessons to understand better the strategies that they were using, the teachers reflected on their own practice. Reflection is an important part of many professionals’ work. Castle and Aichele (1994) felt that, in regard to the work of teachers, “[r]eflective insights provide a deeper and richer understanding of what it means to teach, thus contributing to professional knowledge used to make autonomous decisions” (p. 5). Schön (1983) described this as reflection-in-action where research is happening in context and thinking is not separated from doing.

Schön (1983) wrote that:

• There are actions, recognitions, and judgements which we know how to carry out spontaneously; we do not have to think about them prior to or during their performance.
• We are often unaware of having learned to do these things, we simply find ourselves doing them.
• In some cases, we were once aware of the understandings which were subsequently internalized in our feeling for the stuff of action. In other cases, we may never have been aware of them. In both cases, however, we are usually unable to describe the knowing which our action reveals. (p. 54)

Doing research that requires teachers to think deeply about their teaching practice is usually designed to support teachers to query actions that they would normally do spontaneously. Mason (1994) warned that in developing habits to cope with standard situations, it is possible to become de-sensitised to “possible alternative actions” (p. 3). Reflection-in-action can result in professionals, such as teachers, identifying other ways of operating that may result in improvements to practice.

This type of reflection-in-action is what others have considered to be good professional development. Bolam (1987) felt that professional development was an exploration that teachers undertake in order to improve the teaching and learning that happens in the classroom. It is known that for professional development to be most useful to teachers, then certain conditions need to be met. Professional development must be something which has been chosen by the teacher (Castle & Aichele, 1994) and it needs to be done over a considerable period of time. Begg (1993), in summarising the literature on professional development, stated that “teachers need a considerable time (two or three years) to trial, discuss, reflect on, adopt, and institutionalize significant changes” (p. 84).

During the research at the kura in 1998–99, concerns had been raised about the need for professional development in mathematics (Meaney, 2001).

Teachers wanted more opportunities for updating their mathematics knowledge as well as their knowledge of teaching mathematics. Teachers felt that what was offered presently in Māori by the education system was not challenging enough. (p. 11)

Since this time, Poutama Tau has been instigated as a professional development project that provides teachers with knowledge about the progression of numeracy understandings and pedagogical knowledge (Christensen, 2003). The teachers at the kura saw the scaffolding and modelling research as complementing their work with Poutama Tau. It fulfilled the function of good professional development, because it was chosen by the teachers and occurred over two years.

Traditionally, professional development has focused on either teachers’ pedagogical knowledge or their mathematical content knowledge (White, Mitchelmore, Branca, & Maxon, 2004). This research project could be considered as doing neither and, at the same time, doing both. This is because it was not specifically about mathematics or about mathematics teaching. Instead, it was designed so that teachers could become better aware of how they supported their students to acquire the mathematics register. This awareness led to teachers making changes to their practice so that students could improve their learning of mathematical terms and expressions. This improvement was assumed to lead to students’ mathematical achievement also improving.

However, it is known that changing teachers’ practices is difficult (Jaberg, Lubinski, & Yazujian (2002). There is a need for teachers to construct “their own perspectives on change and [to be provided] with information from research about how students learn” (p. 3). It is, therefore, useful to document how this awareness was gained and the effect that this had on teachers’ classroom practices.

The following sections describe teachers’ reactions to being part of the research process, before going on to describe their perceptions of how researching the scaffolding and modelling aspects of the mathematics register had had an effect on their teaching practice. The data for these sections came from the notes of the meeting held in 2006, notes from interviews with the teachers, and surveys completed by teachers in August 2006. As well, T1’s written reflections on her 2006 videotaped lessons are provided in Appendix C, and are referred to in the section on teachers’ practice. The final section describes the repetition of vocabulary and compares the proportions of mathematical to nonmathematical terms for each teacher in 2005 and 2006. It uses the transcripts from the videotaped lessons in both years.

Involvement in the research process

The research process was challenging for some of the teachers, but most found that it supported their reflection process. This reflection also resulted in the teachers offering suggestions for improving the data collection and analysis so that the findings would be more valuable to them.

Almost all of the teachers found being videotaped daunting. This apprehension had been one of the reasons it had been decided that sharing of the videotapes with other teachers would not be a major part of this research as it had in projects such as that described by Siemon and Virgona (2003). Instead, when the project was initially discussed, it was decided that it would be up to the teachers if and when they would share extracts from their lessons with others. However, as T5 described it, once teachers realised that the videotaping was not “Big Brother”, they were able to use the videotapes to improve their teaching.

Two teachers admitted to thinking more about what they were teaching when planning the lessons that would be videotaped. For one of these teachers, this was because he was aware he would watch them with a university-researcher and was conscious of not wanting to present himself poorly. As someone new to teaching as well as to the kura, it had been quite a shock to find himself being videotaped in his first term as a teacher. The other teacher found that having her lessons videotaped forced her to reflect on the progression of the lessons that she was presenting.

If you were teaching a similar one to the previous lesson, [the videotaping] made you think about why it needed to be similar. If it was different it made you think about why and how you had moved the focus on. This meant that you were thinking about how you were moving the children on mathematically. Sometimes when you were busy with your teaching, you did not think too much about ensuring that the children were moving mathematically on. (T6)

This teacher’s comments show how the process of being videotaped had in itself made her reflect upon those actions that she would normally carry out spontaneously. Although none of the other teachers explicitly mentioned similar considerations, it was likely that they also thought carefully about the lessons that would be videotaped. T1 mentioned, at the April 2006 meeting, that she “will be better prepared for the next filming”. It, therefore, seems that videotaping lessons contributed to teachers using reflection-in-action.

Although the teachers also had been apprehensive about watching the videotapes, most found the experience rewarding. One teacher, at the April 2006 meeting, stated that:

Transcriptions were a big surprise. However, after going over it, I felt good about what was going on. A lot of mathematical lexicon needs to be mastered. Starting to see what I need to look at. (T1)

Another teacher found that having the time to step back and look at the videotapes gave him a better understanding of what was going on in the classroom.

When you have the time, you get a better idea of what we are actually saying. (T5)

However, at least one teacher expressed her uncertainty about how watching the videotapes would lead to improvements in her own teaching.

In the second year of the project, teachers were more aware of how they could control what would be videotaped so that it gave them the most benefit. Some of them chose to record lessons that they felt would provide them with the most information about their own scaffolding and modelling strategies. T1 had the last of her 2006 videotaped lessons be of two of her students giving and receiving a set of instructions for a geometric construction. She had wanted this because she felt it would provide her with information about whether she had succeeded or failed in her teaching. For the students to be “able to be videotaped on their own, giving instructions and following instructions means that the students need to have the vocabulary and the drawing skills”. It would seem that having the research project extend over two years provided opportunities for teachers to take advantage more fully of adapting the research to their growing awareness of their reflection-in-action needs. Although Castle and Aichele (1994) highlighted the need for teachers to have choice in professional development, it may be that unless professional development occurs across a considerable period of time, teachers may be unable to fully utilise this choice.

Although the teachers generally overcame their initial uncertainties about having their lessons videotaped, they had a number of suggestions for improving the collection and analysis of videos. Some of these suggestions were discussed in the methodology chapter. Of the points mentioned, some were acted upon in 2006 and others will be taken on board for the next project. The points that the teachers raised were:

• the analysis needs to be closer in time to videotaping
• transcriptions without punctuation were difficult to follow
• too much background noise on the videotapes made them difficult to follow at times
• lesson plans needed to be attached to the transcripts
•  securing a person to do the filming and a transcriber was problematic and time consuming
• it was beneficial to have a reliever to look after the class so that the teacher could be videotaped with a group outside of the classroom
• analysis needs to include more than just the words in the transcripts, as body language can also provide information.

Although the teachers, at the beginning, found being videotaped daunting, it did begin the process of reflection. This reflection on teaching continued with the analysis. Consequently, the teachers found this part of the research process very rewarding. The teachers also offered a number of suggestions for how the videotaping and analysis could be improved. Having the project continue for a second year meant that the teachers were able to move beyond the concerns of the first year and choose to videotape lessons that they wanted to learn something from. This supports Begg’s (1993) point that professional development needs to be sustained over time for change in teaching practice to be absorbed by teachers.

Impact on teaching practice

Almost all of the teachers reported some effect on their teaching practice from being involved in the research process. This effect began with an awareness of what they were currently doing and led to a reflection on what they may be able to change in their own classrooms. For some teachers, implementation of change could be seen in their 2006 videotaped lessons, and the teachers further reflected on how they perceived these changes.

Teachers found that watching their videotapes gave them a range of insights about their own teaching. For some teachers, watching their teaching gave them a general awareness about their teaching. T3 stated that she had enjoyed watching “how she interacts with the children and how the individuals act within the class”.

Teachers also found that being involved in the research gave them an increased awareness of the role of language in learning mathematics. T4 stated that:

I have never really thought of maths as a language. I knew it on the surface but it hasn’t really sunk in until we started the project. I see it as a whole new language to learn. Very cool.

As a consequence, she believed that she was a lot more thoughtful about how she explained things to the students and the words that she used. In the 2005 videotaped lessons, she had seen herself giving four different explanations for the same thing and felt that this would have confused the children. She had made changes to how she explained concepts as a direct result of seeing herself on videotape.

Being involved in the research process made the teachers familiar with the Mathematics Register Acquisition model and how the strategies that they used fitted into this model. T2 felt that he had become more open to new strategies and methods. Becoming aware of these meant that he “notice[d] more about what was being taught”. T1 found that the different stages in the model resonated with the different types of strategies needed to support students of different ability levels in her class. Consequently, she was comfortable with her teaching approach. However, she also noted that she was not clear about “exactly what strategies are used quite frequently”.

The teachers used their awareness of their teaching, scaffolding, and modelling strategies, and the Mathematics Register Acquisition model as a starting place for reflecting on how they could improve their practice. For example, T6 stated that she “can see where changes need to be made”. The teachers discussed what they wanted to change, and after the 2006 videotapes had been analysed talked about what changes they had made. T1’s reflections on her 2006 lessons are provided in Appendix C. These show quite clear consideration of the need for students to learn particular aspects of the mathematics register in their mathematics lessons.

T7 had made changes to his teaching as a result of watching the 2005 videotapes of his lessons. He was more conscious of providing explicit teaching of new vocabulary. In 2006, he consistently put a list of vocabulary up on the board to accompany each new unit. Previously he had done this on an ad hoc basis. He also engaged in discussions about vocabulary usage with his students, so that when there was a choice of words, the most appropriate choice was made. Another change that he was in the process of making was that he was trying harder to use complete sentences rather than just using phrases. The students were also expected to provide complete sentences. As a consequence of being involved in the project, he was “more observant of others’ use of language as a result of considering the 4 stages of language learning”.

T5 also expected more structured responses from his students in 2006. In the Poutama Tau programme, there is an expectation that students provide explanations of their thinking. However, he was aware that he had not stringently adhered to the requirement to ask “how do you know” and even when he had done so, he had accepted responses such as “just because I know” and “because it just is” from his students. Now his students were giving explanations as a normal part of what they did in mathematics, although they were still not regularly using logical connectives. This was something that he wanted to work on further. He described being involved in the project as “brilliant”.

As a consequence of her involvement, T6 was teaching mathematics lessons purely focused on aspects of the mathematics register:

Previously the lesson focus had been on the maths concept with an expectation that a five minute discussion of language was sufficient for children to gain it. As well the language given in an explanation might have been wordier and therefore more difficult for students to understand. Being aware of the issue of language meant that [I] was now simplifying how [I] explained ideas.

She felt that the changes that she had incorporated into her lessons had resulted in the students gaining the language more quickly. By watching what she did in the 2006 videotapes, she was able to see how doing something differently had come across to the students. She was able to identify what had worked well and think about why this had worked.

The teachers also raised some points about what they needed in order to improve their teaching. T2 stated that he wanted “a database of words, and a type of thesaurus of the maths language and construction”. As a beginning teacher, he struggled with becoming familiar with what were the appropriate aspects of the mathematics register that he should be using with his students.

Part of the research process involved having regular meetings to discuss what had been done and what would be done in the future. T1 commented on the learning that came from these meetings. She felt that it was good to have information shared across year levels so that that there was a transition from the junior to senior school about awareness of the mathematics register. T5 was also conscious of the need to know what was needed in Tau 7 and 8 so he knew what his students required for their next level of mathematics learning. He felt that the project was contributing to him gaining a broader picture of where the students were at and where they were moving to.

As well as being asked to comment on their perceptions of their own teaching practice, teachers were asked to comment on the effect of the project on their students’ mathematical understandings. T1 believed that every student had improved at least in some way because of the way that she structured the classroom activities and from having the students produce written responses to the activities. Appendix C provides T1’s commentary on her 2006 lessons. These clearly show how both aspects were incorporated into her lessons. T4 commented that she felt that her students’ mathematical understandings had improved because she was now presenting ideas “in a way that they may be able to pick it up easier”. T2 believed that learning occurred through conversations. Therefore, if his students had a better understanding of the language, they were more likely to be learning.

The comments made by the teachers showed that they felt that being part of the project had had a positive effect on their teaching. This suggests that the analysis of their videotaped lessons had contributed to them reflecting-in-action. It would also seem that being involved in a two-year project was important as it gave them time to think about their current practices. It also provided them with time to implement changes to their practices based on this reflection. Given that the teachers believed that they had changed their own use of the mathematics register, it seemed useful to investigate whether this change had manifested itself in their use of mathematical vocabulary. The final section of this chapter compares the use of specific terms in teachers’ 2005 lessons with their use in the 2006 lessons.

Mathematical vocabulary use in the classrooms

It was decided to investigate whether teacher’s perceptions about the changes that they had implemented in their classrooms could be identified through an examination of the lesson transcripts. As discussed in Chapter 2, it was decided to compare the number of words that the teachers and students repeated more than seven times in the 2005 lessons to the 2006 lessons. Seven uses of the word was chosen because second language learners need to hear a word seven times, at spaced intervals, to acquire it (Thornbury, 2002, cited in McNaughton et al., 2006). We anticipated that an increased awareness about the mathematics register and how it was acquired would result in teachers repeating a greater proportion of mathematical words compared to nonmathematical words in the 2006 lessons than they had in the 2005 lessons.

However, the practicalities of making such a comparison were quite difficult. One of the issues was that the lessons varied between six and 40 minutes in length and were on very different topics. It was rare for the teacher to be recorded teaching lessons on the same topic in both years. Part of the reason for this was that the mathematics programme ran on a two-year cycle and some topics would not be taught in both years. It was, therefore, decided that comparing the proportions of mathematical to nonmathematical words would be one way of overcoming these differences.

Although it was easy to classify numerals as mathematical words, it was not always clear whether some words should be classified as mathematical or nonmathematical. Words such as mahi often referred to mathematical work, but would be considered as a more general classroom word than a mathematical term.

As well, it was clear that this was a very rough measure of the mathematical nature of a lesson. For example, T2’s lessons often consisted of him giving a word problem that students had to model with counters and then determine an answer. In these cases, it was not so much individual words that the teacher wanted students to learn, but the structure of story problems. These lessons, therefore, look like they were not mathematical in nature, but, in fact, if another measure was used, such as mathematical grammatical expressions, then a different set of results would be seen. However, as a start for searching for a way of identifying the effect on classroom practices, comparing the number of mathematical and nonmathematical words did provide us with some data.

The tables show the ratio of mathematical to nonmathematical words used by students and by teachers seven or more times. A total is also given and this is often more than the addition of the students and teacher amounts. This is because students may say the word three times while the teacher may say it five times. During the course of the lesson, the word is said more than seven times, but not by just one group of people. Each table shows the ratio for each lesson for a particular teacher and will be discussed separately. A final section discusses the overall trend for the vocabulary repetition.

Table 3 T1’s ratio of mathematical to nonmathematical vocabulary

T1		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	1.0	10.2	16.2	1.2	4.13	11.14
2	1.0	3.6	5.7	0.0	6.4	7.5
3	4.0	8.5	11.5	0.0	6.4	8.5
4	1.1	2.4	10.6	1.2	6.11	12.13
5	2.1	1.2	4.6	1.1	1.3	6.6

Table 3 shows the results for T1’s lesson. In 2005, in three of the lessons, more mathematical words than nonmathematical words were repeated seven times. In the remaining two lessons, very few words were repeated, with slightly more nonmathematical words being repeated than mathematical words. In 2006, the amounts of mathematical to nonmathematical words had little difference between them. In both year levels, it is more often the teacher who repeated the words and this was especially the case for the nonmathematical words. Very few words were said seven or more times by the students. It could not be said that the amount of mathematical words repeated had increased in T1’s classroom in 2006.

Table 4 T2’s ratios of mathematical to nonmathematical vocabulary

T2		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	5.0	5.9	9.9	2.5	7.15	8.17
2	2.0	1.3	7.3	2.4	6.9	8.12
3	11.1	15.21	20.23	2.5	6.17	8.19

The repeated words in T2’s classroom can be seen in Table 4. This shows that the proportion of mathematical words went down in the 2006 lessons. The students did contribute more of the repeated words than those seen in T1s classrooms.

Table 5 T3’s ratios of mathematical to nonmathematical vocabulary

T3		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	12.0	18.27	24.27	6.0	8.1	16.1
2	4.0	7.8	15.9	5.0	4.4	10.4
3	10.0	11.16	16.16	8.0	4.3	15.3
4				1.1	4.2	5.3

In Table 5, the proportion of mathematical words to nonmathematical words in 2006 had increased greatly, except for lesson 4. As was the case with the other Year 0 teacher, T2, the students were repeating quite a number of the mathematical words. In 2006, they repeated more mathematical words than the teacher in two lessons.

Table 6 T4’s ratios of mathematical to nonmathematical vocabulary

T4		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	0.0	0.4	0.6	8.0	7.2	10.2
2	0.2	1.17	1.20	9.0	2.0	12.1
3				6.0	1.1	7.1

T4 was another teacher in the junior school. Her 2005 lessons had been on having students learn ideas about probability using the context of Little Red Riding Hood. This seems to have resulted in very few mathematical words being repeated frequently. However, her 2006 lessons showed a far greater proportion of mathematical words being used. Most of the repeated words were said by students rather than by the teacher. T4 had been a teacher who had stated that she was much more conscious from watching the 2005 videotaped lesson of how she used mathematical language with the students. It would seem that this awareness has manifested itself in ensuring that consistent mathematical language was used.

Table 7 T5’s ratios of mathematical to nonmathematical vocabulary

T5		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	0.0	4.2	6.2	4.1	7.5	18.6
2	5.0	19.19	22.20	4.11	0.1	4.11
3	13.8	0.0	30.8	4.7	2.1	9.10

The results, shown in Table 7 for T5, show no clear pattern. In 2005, more mathematical words were repeated than nonmathematical words. However, the numbers of the two types of words were very similar for lesson 2. In 2006, one lesson had a greater number of mathematical words while the next lesson showed exactly the opposite. The third lesson had an almost equivalent proportion of mathematical to nonmathematical words. Students did contribute quite a considerable number of the repeated words in both years.

Table 8 T6’s ratios of mathematical to nonmathematical vocabulary

T6		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	3.2	12.16	12.17	10.6	15.19	29.24
2	6.7	13.10	14.11	0.1	13.5	15.6
3	4.1	10.12	14.12	3.1	6.3	11.6
4	6.0	8.6	12.7

Table 8 also shows no clear pattern in the distribution of repeated words in the lessons that were videotaped in 2005. Generally, the amounts were fairly similar, although in four lessons, more mathematical words were repeated than nonmathematical. However, in 2006 consistently more mathematical words were repeated than nonmathematical words. As was the case with several other teachers, the students did contribute a significant amount of the repeated words. In these lessons, it was non-mathematical as well as mathematical.

Table 9 T7’s ratios of mathematical to nonmathematical vocabulary

T7		2005			2006
Lesson	Students	Teacher	Total	Students	Teacher	Total
1	4.2	17.17	19.16	0.0	3.4	4.4
2	8.4	19.23	24.26	0.0	2.8	2.9
3				0.1	14.11	16.13

Table 9 shows the results for T7’s lessons. The amounts of mathematical words compared with nonmathematical words that were repeated more than seven times were similar in most lessons. As was the case with T1, it cannot be said that participation in the project resulted in the proportion of mathematical words increasing in the 2006 lessons. The number of words that were repeated more than seven times was much greater in 2005 than the 2006. However, only two lessons were saved from the 2005 recordings and it may be that these are not representative.

It had been anticipated that the proportion of mathematical words repeated in the 2006 lessons would be greater than nonmathematical words. This was the case in the junior classes, but not the case for the intermediate and high school classes. It may be that the most experienced teachers were operating in these senior classes and their teaching involved more written recording of mathematical activity. This recording would also contribute to the repetition of words, but because it was not kept and cannot be included in the counting of words for these tables. It may also be that analysis done of the words repeated seven or more times in the lessons is not a very useful way of determining whether changes had occurred in teachers’ practice. Further investigation needs to be undertaken to see how change in regard to how teachers support mathematics register acquisition can be documented.

Summary

The teachers found that being involved in the project did contribute to them reflecting on their own practice. Most of the teachers felt that this had resulted in them making changes to the way they taught the mathematics register. This was considered as contributing to increasing students’ mathematical understandings. It was anticipated that there would be a perceivable effect on teachers’ classroom practices. However, investigations of the proportions of mathematical to nonmathematical words repeated more than seven times did not produce a clear picture. It would seem that the junior teachers had increased the proportion of mathematical words repeated in their lessons, but a similar result was not seen in the senior classrooms.

6. Project team

At Kura Kaupapa Māori o te Koutu, the following teachers were part of the project team:

• Aroha Fairhall
• Tracy Best
• Ngāwaiata Sellars
• Kataraina Pakikinga
• Ranara Leach
• Horomona Horo.

Heeni Maangi and Anahera Katipa joined the project in 2006, but videotapes of their lessons were not included as data because they did not have 2005 lessons to be compared with.

The research team was:

• Uenuku Fairhall, Principal of Kura Kaupapa Māori o te Koutu
• Tony Trinick, Associate Dean Māori at the University of Auckland’s Faculty of Education
• Dr Tamsin Meaney, Senior Lecturer, University of Otago.

7. Limitations

A number of issues meant that the project did not always run smoothly. These included having limited funded researcher time and difficulties in collecting and transcribing videotapes. There were also difficulties in providing teacher release days because of a lack of relief teachers available in kura kaupapa generally.

TLRI funding rules meant that because the research was only occurring in one school, we were restricted to C level funding ($40,000 for each year). However, we were working with teachers in Year 0 to Year 13 mathematics classrooms who taught about 170 students. The amount of data we collected was necessary so that each teacher could consider their own teaching, but with limited funded researcher time it was an enormous amount to analyse and write up. Although the level of funding for C projects has now increased to $50,000, it is still difficult to do research with this range of age groups and number of teachers. In considering future funding for projects that are run across multiple age groups, it may be more appropriate to provide B level funding so that appropriate comparisons can be made across classes and a comprehensive policy developed across the whole kura.

The videotaping in classrooms turned out to be far more difficult than had been anticipated. We wanted five videotapes to be taken of each class. In 2005, only one teacher ended up with five lessons that could be analysed. In 2006, more lessons were recorded, but only two teachers managed to record five lessons and one of these left the kura before her lessons could be analysed. It is clear from watching the five lessons of T1’s classroom from 2005 that responsibility for using new aspects of the mathematics register did move from the teacher to the students. However, it was not possible to show clearly how this happened without doing a longitudinal study. This would have required more funding and may not have fulfilled the teachers’ needs as well as the current study has done. However, it must be considered a limitation on the study that this data was not gathered, and we can, in fact, say nothing about the effect of what the teachers did on students’ learning.

We had also expected to videotape the classrooms from two angles and to have a record of any work done on the board or worksheets handed to students. It was difficult to find a regular camera person who could take videos and keep a record of board notes. Although, eventually we were able to make recordings in all of the teachers’ classrooms, board notes were not kept. The classrooms were also very difficult to record in. Background noise meant that the recordings were often difficult to understand. This was particularly problematic in the junior classes where often the teachers worked with one group while other students worked on individual tasks. The videotapings were also done on small tapes that had to be rendered onto CDs so that they could easily be played back to the teachers and so that they could be sent to the transcriber. However, the rendering not only took longer than originally thought, but also resulted in the loss of some videotapes. By the end of the project, another video camera had been purchased which records straight to a DVD with an external microphone shoe so that a wireless microphone could be placed anywhere in the classroom. This will be of benefit for the next project. However, the limitations on data collection did affect the results from this project.

Transcribing the videotapes had been seen as a valuable resource for helping the teachers analyse the videotapes with the researchers. However, it was difficult to find someone who was fluent in te reo Māori and understood sufficient mathematics to be capable of transcribing the classroom videotapes. This combination of skills and interests were very difficult to find. Consequently, a range of people was used, and the time it took for getting this work done delayed being able to analyse the videotapes. As was discussed in Chapter 5, this meant that the analysis of the teachers’ lessons was not considered as valuable as it may have been by the teachers. It is difficult to know how this issue could have been overcome or can be overcome in the future. In 2006, we analysed the videotapes before the transcripts had been done. However, this made it much more difficult to produce an in-depth description for publication, although it was more beneficial for the teachers. For the 2007 TLRI project, we have found a research assistant to support the videotaping and who has been mentored in doing transcriptions while working with others on transcribing the final 2006 videotapes. If research is to be carried out in kura kaupapa, there is a need as a research community to increase the research capability in this area in order for the work to be of most benefit to the teachers and to others.

Another limitation was the level of te reo Māori spoken by the lead researcher. Although both Tony Trinick and Uenuku Fairhall are fluent speakers, the extra demands on their time meant that they were not able to spend much time working with the teachers on the analysis of the videotapes, and the bulk of this work fell on Tamsin Meaney. The situation was further complicated by her having to have major surgery in Term 3, 2005, so that she was then unable to visit the kura and provide support to the teachers. By not having a fluent te reo Māori speaker as the university-researcher, the teachers realised that it was necessary for them to be active analysers of the videotapes, and Tamsin’s role became one of asking questions about what was happening and recording the analysis. This situation had benefits for the research capability of the teachers. However, working with a fluent speaker may have resulted in the subtleties of the language being understood better.

Another issue that we faced in doing the analysis with the teachers was a lack of relief teachers, especially in 2005. This is a continual difficulty for kura kaupapa throughout New Zealand, and although it was alleviated in 2006 by the availability of a relief teacher to the kura, it will continue to be an issue for other research in kura kaupapa. Originally, it was envisaged that teachers could be released for hui on the project and to do their analysis. However, the number of teachers involved in the project meant that it was impossible to replace them all for a hui. Consequently, hui were generally held in school holidays or on weekends. It also meant that analysis had to be done in teachers’ release time, making the analysis piecemeal as this was a limited period of time.

It also put extra pressure on teachers who still needed to do class preparation. Once again, this issue is not easy to resolve, but it had an impact on the research.

Although the research collected an enormous amount of data and has produced some fascinating results, a number of limitations has meant that it had some very stressful moments as we tried to keep the project on track. Extra value from the project could be gained by providing more funding so that the researchers could have more time to analyse the extra data that was collected and to write in more detail about the analysis that had been done. Notwithstanding this, the teachers felt that being involved in the project had raised their awareness about their teaching of te reo tātaitai. We also feel that the results will be of interest and benefit to other teachers of mathematics in Māori immersion programmes. We would, therefore, like to once again express our appreciation for the TLRI funding that we received and state that we feel that New Zealand is to be congratulated for providing research funding for teacher-initiated projects.

References

Alton-Lee, A. (2005, May). Quality teaching for diverse learners: How an evidence-based approach can help. Keynote address to Australian Curriculum Studies Association Forum (ACSA), Quality teachers: Quality teaching – Creating a new agenda for action by practitioners, researchers and policy makers, Melbourne.

Anghileri, J. (2002). Scaffolding practices that enhance mathematics learning. In A. Cockburn & E. Nardi (Eds.), Proceedings of the 26th Annual Conference of the International Group for the Psychology of Mathematics Education (Vol 2, pp. 49–56). Norwich, UK: UEA.

Anthony, G., & Walshaw, M. (2006, forthcoming). Best evidence synthesis: Characteristics of pedagogical approaches that facilitate learning for diverse learners in early childhood and schooling in pāngarau/mathematics. Wellington: Ministry of Education.

Au, K. H. (1980). Participation structures in a reading lesson with Hawaiian children: Analysis of a culturally appropriate instructional event. Anthropology and Education Quarterly, 11(2), 91–115.

Barnes, D. (1992). From communication to curriculum. Portsmouth, UK: Boyton/Cook.

Barton, B., & Fairhall, U. (1995). Is mathematics a Trojan horse? Mathematics in Māori education. In B. Barton & U. Fairhall (Eds.), Mathematics in Māori education (pp. 1–12). Auckland: University of Auckland.

Barton, B., Fairhall, U., & Trinick, T. (1998). Tikanga reo tatai: Issues in the development of a Māori mathematics register. For the Learning of Mathematics, 18(1), 1–17.

Begg, A. (1993). Professional development of high school mathematics teachers: Final report for the Research Division of the Ministry of Education. Hamilton: University of Waikato.

Berry, J. (1985). Learning mathematics in a second language: Some cross-cultural issues. For the Learning of Mathematics, 5(2), 18–21.

Bickmore-Brand, J., & Gawned, S. (1990). Scaffolding for improved mathematical understanding. In J. Bickmore-Brand (Ed.), Language in Mathematics (pp. 43–51). Melbourne: Australian Reading Association.

Bill, V. L., Leer, M. N., Reams, L. E., & Resnick, L. B. (1992). From cupcakes to equations: The structure of discourse in a primary mathematics classroom. Verbum, 1–2, 63–85.

Bolam, R. (1987). What is effective INSET?, In Professional Development and INSET: Proceedings of the 1987 NFER Members Conference (pp. 38–53). Slough, UK: National Foundation for Education Research.

Brenner, M. E. (1985). Arithmetic achievement at Ka Na’i Pono: 1984 results from standardized testing. Technical Report No. 126. Honolulu: Centre for Development of Early Education.

Brenner, M. E. (1998). Adding cognition to the formula for culturally relevant instruction in mathematics. Anthropology and Education Quarterly, 29(2), 214–244.

Brett, A., Rothlein, L., & Hurley, M. (1996). Vocabulary acquisition from listening to stories and explanations of target words. The Elementary School Journal, 96(4), 415–422.

Burton, L., & Morgan, C. (2000). Mathematicians writing. Journal for Research in Mathematics Education, 31(4), 429–453.

Castle, K., & Aichele, D. B. (1994). Professional development and teacher autonomy. In D. B. Aichele & A. F. Coxford (Eds.), Professional development for teachers of mathematics 1994 Yearbook (pp. 1–8). Reston, VA: National Council of Teachers of Mathematics.

Chapman, A. (1997). Towards a model of language shifts in mathematics learning. Mathematics Education Research Journal, 9(2), 152–172.

Christensen, I. (2003). Exploring issues in mathematics education. Wellington: Ministry of Education.

Christensen, I, Trinick, T., & Keegan, P. J. (2003). Pāngarau curriculum framework and map. Technical Report No. 38, Project asTTle. Auckland: University of Auckland.

Clarke, D. (2001). Complementary accounts methodology. In D. Clarke (Ed.), Perspectives on practice and meaning in mathematics and science classrooms (pp. 13–32). Dordrecht: Kluwer Academic.

Eisenhart, M. A. (1988). The ethnographic research tradition and mathematics education research. Journal for Research in Mathematics Education, 19(2), 99–114.

Ellerton, N., & Clements, M. K. (1996). Researching language factors in mathematics teaching and learning: The Australasian contribution. In B. Atweh, K. Owens, & P. Sullivan (Eds.), Research in Mathematics Education in Australia 1992–1995 (pp. 191–235). Sydney: Mathematics Education Research Group of Australasia (MERGA).

Elley, W. B. (1989). Vocabulary acquisition from listening to stories. Reading Research Quarterly, 24(2), 174–187.

Fetterman, D. (1993). Words as the commodity of discourse: Influencing power. In D. Fetterman (Ed.), Speaking the language of power: Communication, collaboration and advocacy (Translating ethnography into action) (pp. 1–18). Washington DC: Falmer Press.

Gibbons, P. (1998). Classroom talk and the learning of new registers in a second language. Language and Education, 12(2), 99–118.

Gibbs, W., & Orton, J. (1994). Language and mathematics. In A. Orton & G. Wain (Eds.), Issues in mathematics (pp. 95–116). London: Cassell.

Graham, B. (1988). Mathematical education and Aboriginal children. Educational Studies in Mathematics, 19(2), 119–135.

Jaberg, P., Lubinski, C., & Yazujian, T. (2002). One teacher’s journey to change her mathematics teaching. Mathematics Teacher Education and Development, 4, 3–14.

Kermani, H., & Brenner, M. E. (1996, April). Maternal scaffolding in the child’s Zone of Proximal Development: Cultural perspectives. Paper presented at the American Educational Research Association, New York.

Khisty, L. L., & Chval, K. B. (2002). Pedagogic discourse and equity in mathematics: When teachers’ talk matters. Mathematics Education Research Journal, 14(3), 154–168.

McNaughton, S., MacDonald, S., Barber, J., Farry, S., & Woodard, H. (2006). Ngā taumatua. Wellington: Ministry of Education. Retrieved 26 August 2006, from http://www.minedu.govt.nz/ index.cfm?layout=document&documentid=10606&data=

Mason, J. (1994). Professional development and practitioner research in mathematics education. Chreods, 7, 3–12.

Meaney, T. (2001). An indigenous community doing mathematics curriculum development. Mathematics Education Research Journal, 13(1), 3–14.

Meaney, T. (2002). Aspects of written performance in mathematics learning. In K. Irwin, B. Barton, M. Pfannkuch, & M. Thomas (Eds.), Mathematics in the South Pacific: Proceedings of the 25th Mathematics Education Research Group of Australasia conference (pp. 481–488). Auckland: University of Auckland.

Meaney, T. (2004, November). Ways and means to understand the linguistic choices of children’s mathematical explanations. In Turning the kaleidoscope: Proceedings of the New Zealand Association of Research in Education conference. Wellington.

Meaney, T. (2005). Mathematics as text. In A. Chronaki & I. M. Christiansen (Eds.), Challenging perspectives in mathematics classroom communication, (pp. 109–141). Westport, CT: Information Age.

Meaney, T. (2006a). Acquiring the mathematics register in classrooms. set: Research Information for Teachers, 3, 39–43.

Meaney, T. (2006b). Really that’s probably about roughly what goes down: Hesitancies and uncertainties in mathematics assessment interactions. Language and Education, 20(5), 374–390.

Meaney, T., Fairhall, U., & Trinick, T. (2006, February) The role of language in ethnomathematics: Does the language make it ethnomathematics? In the Proceedings of the Third Ethnomathematics Conference, Auckland. Retrieved 26 August 2006, from http://www.math.auckland.ac.nz/ ~poisard/ICEm3/ICEm3.html.

Mehan, H. (1979). Learning lessons: Social organization in the classroom. Cambridge, MA: Harvard University Press.

Meyer, D. K., & Turner, J. C. (2002). Using instructional discourse analysis to study the scaffolding of student self-regulation. Educational Psychologist, 37(1), 17–25.

Moskal, B. M., & Magone, M. E. (2000). Making sense of what students know: Examining the referents, relationships and modes students displayed in response to a decimal task. Educational Studies in Mathematics, 43(3), 313–335.

Mousley, J. (1999). Perceptions of mathematical understanding. In J. M. Truran & K. M. Truran (Eds.), Making the difference: Proceedings of the 22nd Annual Conference of the Mathematics Education Research Group of Australasia. Adelaide: Mathematics Education Research Group of Australasia (MERGA).

Nathan, M. J., & Knuth, E. J. (2003). A study of whole classroom mathematical discourse and teacher change. Cognition and Instruction, 21(2), 175–207.

Nelson-Barber, S., & Estrin, E. (1995). Culturally responsive mathematics and science education for native students. San Francisco: Regional Educational Laboratory Network.

Noridah, A., & Clements, M. A. (1999). The language of mathematics: Educational consequences of definitional and notational variations. M. A. Clements & Y. P. Leong (Eds.), Cultural and language aspects of science, mathematics and technical education. Darussalam: University Brunei.

Otterburn, M., & Nicholson, A. (1976). The language of (CSE) mathematics. Mathematics in School, 5(5), 18–20.

Pintrich, P. R. (2000). The role of goal orientation in self-regulated learning. In M. Boekaerts, P. R. Pintrich, & M. Zeidner (Eds.), Handbook of self-regulation: Theory, research and applications (pp. 452–502). San Diego, CA: Academic Press.

Reason, P. (1994). Three approaches to participatory inquiry. In N. K. Denzin & Y. S. Lincoln (Eds.), Handbook of qualitative research (pp. 324–339). Thousand Oaks, CA: Sage.

Roberts, T. (1998). Mathematical registers in Aboriginal languages. For the Learning of Mathematics, 18(1), 10–16.

Rogoff, B. (1988). The joint socialisation of development by young children and adults. In A. Gellatly, D. Rogers, & J. A. Sloboda (Eds.), Cognition and social worlds (pp. 57–82). Oxford: Oxford University Press.

Schön, D. (1983). The reflective practitioner. New York: Basic Books.

Siemon, D., & Virgona, J. (2003, November–December). Identifying and describing teachers’ scaffolding practices in mathematics. In Educational research: Risks and dilemmas: Proceedings of the New Zealand/Australian Association of Research in Education conference. Auckland: University of Auckland.

Skemp, R. (1971). The psychology of learning mathematics. London: Penguin.

Smith, G. H. (1990). The politics of reforming Māori education: The transforming potential of Kura Kaupapa Māori. In H. Lauder & C. Wylie (Eds.), Towards successful schooling (pp. 73-89). London: Falmer Press.

Spolsky, B. (2003). Reassessing Māori regeneration. Language in Society, 32(4), 553–578.

Tanner, H., & Jones, S. (2000). Scaffolding for success: Reflective discourse and the effective teaching of mathematical thinking skills. In T. Rowland & C. Morgan (Eds.), Research in mathematics education, Volume 2: Papers of the British Society for Research into Learning Mathematics (pp. 19–32). London: British Society for Research into Learning Mathematics.

Thornbury, S. (2002). How to teach vocabulary. Harlow: Longman.

Tobin, K. (1983). The influence of wait-time on classroom learning. European Journal of Science Education, 5(1), 35–48.

Wells, G. (1999). Dialogic inquiry: Towards a sociocultural practice and theory of education. Cambridge, UK: Cambridge University Press.

White, D. Y. (2003). Promoting productive mathematical discourse with diverse students. Mathematical Behaviour, 22(1), 37–53.

White, P., Mitchelmore, M., Branca, N., & Maxon, M. (2004). Professional development: Mathematical content versus pedagogy. Mathematics Teacher Education and Development, 6, 49–60.

Whitland, J., & Pegg, J. (1999). Exploring diversity: Year 2 students responses to questions concerning simple 2D shapes. In J. M. Truran & K. M. Truran (Eds.), Making the difference: Proceedings of the 22nd annual conference of the Mathematics Education Research Group of Australasia. Adelaide: Mathematics Education Research Group of Australasia (MERGA).

Williams, S. R., & Baxter, J. A. (1996). Dilemmas of discourse-orientated teaching in one middle school mathematics classroom. The Elementary School Journal, 97(1), 21–38.

Wood, D., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychology and Psychiatry, 25, 89–100.

Wood, T. (1998). Alternative patterns of communication in mathematics classes: Funneling or focusing? In H. Steinbring, M. G. B. Bussi, & A. Sierpinska (Eds.), Language and communication in the mathematics classroom. Reston, VA: National Council of Teachers of Mathematics (NCTM).

 

The appendices for this online version of the report have been removed. However, you can access them here

Acknowledgements

This project would not have been possible without the active support of the kaiako of Te Kura Kaupapa o Te Koutu: Aroha Fairhall, Tracy Best, Ngāwaiata Sellars, Kataraina Pakinga, Ranara Leach, and Horomona Horo. In 2006, Heeni Maangi and Anahera Katipa joined the staff and instantly became project teacher-researchers. We also need to thank the tamariki and their whānau. Without their participation and active support, there would not be a project to report on.

The project also called on the skills of a number of people to help ensure its completion. These people were: Taitimu Heke-Sellars, Ruakiri Fairhall, Sonya Daly, Kelly Holtermann ten Hove, Abby Suszko, Marty Schaff, Lisa Marr, and Mike Atkinson.

We would like to thank Associate Professor Peter Howard and Ms Sharon Cooke, who have considerable experience in mathematics education with indigenous students in Australia. They visited the project team in August 2006 and provided valuable input.

We would also like to thank the Teaching and Learning Research Initiative for providing the funding so that this research could be undertaken. A special thanks goes to Garrick Cooper, who gave active support and suggestions as the project progressed.